
Prinzip des kleinsten Zwanges
Prinzip des kleinsten Zwanges (auch gaußsches Prinzip des kleinsten
Zwanges) ist ein von Carl
Friedrich Gauß 1829 aufgestellter und von Philip
Jourdain ergänzter Satz der klassischen Mechanik, wonach ein mechanisches
System sich so bewegt, dass der Zwang zu jedem Zeitpunkt
minimiert wird.
Der Zwang ist dabei definiert als[1]:
wobei über die Massenpunkte i summiert wird, mit den vorgegebenen
eingeprägten Kräften ,
den Massen der Punktteilchen
und den Beschleunigungen
.
Die einzelnen Punktteilchen, aus denen man sich das System zusammengesetzt
denkt, sind dabei zusätzlichen Zwangsbedingungen unterworfen. Die eingeprägten
Kräfte dürfen explizit von der Zeit, vom Ort und der Geschwindigkeit abhängen,
nicht jedoch von der Beschleunigung.
Bei der Minimierung des Zwanges bezüglich der Beschleunigungen stehen alle
mit den Zwangsbedingungen verträglichen Bewegungen zur Konkurrenz, bei denen zur
Zeit
die Lagen und die Geschwindigkeiten übereinstimmen. Konkurrenz bedeutet, dass
alle möglichen Bewegungen betrachtet werden – auch die, die wegen des Prinzip
des kleinsten Zwanges in der Realität gar nicht auftreten.
In der obigen Gleichung stehen die Differenzen zwischen den Beschleunigungen der Massenelemente und den Beschleunigungen, die sie als freie Massen unter der Einwirkung der an ihnen angreifenden eingeprägten Kräfte erfahren würden. Das Prinzip lässt sich damit wie folgt formulieren:
bzw.
,
mit
(nur die Beschleunigung wird variiert).
Das Prinzip des kleinsten Zwangs ist für sehr allgemein formulierte Zwangsbedingungen gültig. In diese können die Zeit, die Orte und Geschwindigkeiten nichtlinear eingehen. Dadurch grenzt sich das Prinzip des kleinsten Zwangs zum Beispiel vom d'Alembert'schen Prinzip der virtuellen Arbeit ab, bei dem in der einfachsten Fassung holonome Zwangsbedingungen gefordert werden. Cornelius Lanczos[2] nennt es eine geniale Neuinterpretation des d'Alembertschen Prinzips der Mechanik durch Carl Friedrich Gauß, der damit eine Formulierung der mechanischen Prinzipien gefunden hatte, die in der Form seiner Methode der kleinsten Quadrate eng verwandt war.
Beispiel
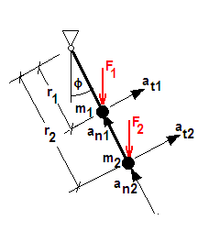
Gegeben ist ein Pendel mit 2 Punktmassen und masseloser starrer Stange (s. Abbildung 1). Die Kräfte Fe1 und Fe2 sind die eingeprägten Kräfte mit den Beträgen m1g und m2g. at1 und at2 sind die Tangentialbeschleunigungen der Massen m1 und m2, an1 und an2 die zugehörigen Normalbeschleunigungen. Der Zwang ist damit:
Bei der Bestimmung des Minimums für obigen Ausdruck ist zu beachten, dass die Variation der Normalbeschleunigungen wegen der gelenkigen Aufhängung verschwindet, während für die Tangentialbeschleunigungen gilt:
und
Somit wird
Wegen der Willkürlichkeit von
folgt nach Kürzung des Faktors 2 die Bewegungsgleichung:
Eine formale Interpretation
Im Folgenden wird eine Interpretation des gaußschen Prinzips für ein allgemeines Punktmassensystem mit Zwangsbedingungen gegeben.
Systembeschreibung
Punktmassen mit Koordinaten
bewegen sich unter Einfluss eingeprägter Kräfte, die von der Zeit, Ort und
Geschwindigkeiten abhängen.
Die Bewegung des freien Systems wird durch die Gleichung
beschrieben (
ist die Massenmatrix), wobei nun der Ort
als zeitabhängige Funktion zu interpretieren ist und
die erste bzw. zweite Zeitableitung sind.
Bei dem zu untersuchenden System sind jedoch
zusätzliche Zwangsbedingungen gegeben
,
die durch die Gleichung
mit einer vektorwertigen Funktion
beschrieben werden.
Mit Hilfe des gaußschen Prinzips soll die Bewegungsgleichung des Systems mit Zwangsbedingungen aufgestellt werden, die an die Stelle der Bewegungsgleichung für das freie System tritt.
Interpretation des gaußschen Prinzips
Das oben verbal formulierte gaußsche Prinzip stellt nicht nur eine
Optimierungsaufgabe dar, sondern eine ganze Familie durch die Zeit
parametrisierter Optimierungsaufgaben, denn der Zwang soll zu jedem Zeitpunkt
ein Minimum annehmen (das ist einer der feinen Unterschiede des gaußschen
Prinzips zum Prinzip
der stationären Wirkung, bei dem die Wirkung
ein von der gesamten Bewegung
abhängiges Funktional ist).
Zu jedem festen Zeitpunkt
konkurrieren alle zweimal stetig im Kurvenparameter
differenzierbaren Kurven
die die Zwangsbedingung
erfüllen, an der Stelle
durch denselben Ort
gehen und dieselbe Geschwindigkeit
haben um das Zwangsminimum.
Zum Aufstellen einer Gleichung für die den Zwang minimierende Bewegung
wird eine im Abschnitt „Ein
Hilfsmittel aus der Analysis reeller Funktionen in einer reellen
Veränderlichen“ des Eintrages zur Variationsrechnung vorgestellte
Methode verwendet.
Aus der Menge aller konkurrierender Kurven wird eine beliebige
reell-parametrige Schar
herausgegriffen, die nach dem Scharparameter
differenzierbar sei. Die Kurve für
,
also
,
soll gerade mit der physikalisch ausgezeichneten Bewegung
übereinstimmen. Das heißt, dass zu jeder Zeit
der vom Scharparameter
abhängigen Zwang
an der Stelle
ein Minimum annimmt (die zweite Darstellung dient im Wesentlichen einer
übersichtlicheren Notation). Hält man die Zeit
fest, so ist
nur noch von
abhängig. Eine notwendige Bedingung dafür, dass diese Funktion bei
ein Minimum annimmt, ist, dass die Ableitung des Zwangs nach
bei
gleich null wird, also
Berücksichtigt man, dass diese Gleichung für jede beliebige gemäß den obigen
Voraussetzungen gewählte Kurvenschar
gelten muss, erhält man daraus die Bewegungsgleichung für das System mit den
vorgegebenen Zwangsbedingungen.
Das wird im nächsten Abschnitt weiter ausgeführt.
Übergang zum jourdainschen Prinzip und zur lagrangeschen Darstellung
Entsprechend der eben skizzierten Vorgehensweise werden nun die Bewegungsgleichungen in einer der Berechnung besser zugänglichen Form aufgestellt. Das dadurch entstehende Gleichungssystem wird auch als jourdainsches Prinzip oder Prinzip der virtuellen Leistung interpretiert.
Zunächst führt man die Differentiation nach
in der letzten abgesetzten Gleichung weiter aus.
Hierbei wurde benutzt, dass viele Terme der inneren Ableitung wegen
und
gleich null sind.
Um zu verdeutlichen, dass in der Klammer die linke Seite der Kräftebilanz für
das freie System steht, wird noch die Massenmatrix
in die Klammer hinein gezogen.
Die mit den Zwangsbedingungen verträglichen Variationen der Beschleunigung
erhält man durch Ableitung der Zwangsbedingung
nach
an der Stelle
und dann nach
.
Hier wurden der Übersicht halber die Argumente weggelassen und mit
die partiellen Ableitungen nach Zeit (i=1), Ort (i=2) und Geschwindigkeit (i=3)
bezeichnet. Bei der anschließenden Differentiation nach
nutzt man wieder aus, dass für
die Variationen von Ort und Geschwindigkeit gleich null sind und erhält die
gewünschte Bedingung dafür, dass
mit den Zwangsbedingungen verträglich ist:
Führt man in der letzten Gleichung und in der letzten Gleichung für
für die Variation der Beschleunigung
das Zeichen
ein und substituiert man (korrekterweise)
und
,
so erhält man letztendlich aus dem gaußschen Prinzip die übliche Schreibweise
für das jourdainsche Prinzip der virtuellen Leistung:
Die physikalisch ausgezeichnete Bewegung
verläuft gerade so, dass zu jedem Zeitpunkt
die Gleichung
für alle
mit
erfüllt ist.
Das kann so interpretiert werden, dass zumindest in den Richtungen ,
in denen sich das System momentan frei bewegen kann, das System mit
Zwangsbedingungen auch die Bewegungsgleichungen des freien Systems erfüllen
muss.
Die Größen
werden als virtuelle Geschwindigkeiten bezeichnet.
Für eine effektivere Berechnung kann man das vorstehende Gleichungssystem wie folgt in die lagrangesche Darstellung (Lagrangegleichung 1. Art) überführen, die auch zum d´Alembert Prinzip äquivalent ist.
Mit der zweiten Gleichung wird ausgedrückt, dass die Menge aller zulässigen
gerade der Kern der Matrix
ist und die erste Gleichung besagt, dass
im orthogonalen Komplement dieser Menge liegt. Insgesamt erhält man also
Denn aus
folgt
.
Es gibt also einen (zeitabhängigen) Vektor
(der Lagrange-Multiplikator), mit dem
gilt (Lagrangegleichungen 1. Art).
Eine Interpretation dafür ist, dass senkrecht zu den möglichen virtuellen
Geschwindigkeiten
beliebige Zwangskräfte
wirken können.
Explizite Ableitung des d'Alembert Prinzips
Holonome
Zwangsbedingungen ,
in denen die Geschwindigkeiten nicht explizit vorkommen, können in die bisherige
Behandlung einbezogen werden, indem man setzt:
Aus der Anschauung ist klar, dass die Zwangsbedingung für den Ort, die das System in eine bestimmte Bahn zwingt, auch die möglichen Geschwindigkeiten einschränkt. Es ergibt sich im jourdainschen Prinzip:
Da danach die Variation der Geschwindigkeiten in den Zwangsflächen erfolgt,
kann man die
durch die virtuellen Verschiebungen
ersetzen und es ergibt sich die übliche Form des d´Alembert Prinzips:
Die physikalisch ausgezeichnete Bewegung
verläuft so, dass zu jedem Zeitpunkt
die Gleichung
für alle
mit
erfüllt ist. Die Lagrangegleichungen 1. Art folgen wie oben:
mit .
Literatur
- Cornelius Lanczos: The Variational Principles of Mechanics. Dover.
Anmerkungen
- ↑ Form nach dem Buch von Cornelius Lanczos, wo der Vorfaktor 1/2 aus der Ableitung aus dem d´Alembert Prinzip stammt, er kann bei anderen Autoren auch wegfallen
- ↑ The Variational Principles of Mechanics, Dover, S. 106


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 25.11. 2020