
Zwangsbedingung
Als Zwangsbedingung wird in der analytischen Mechanik eine Einschränkung der Bewegungsfreiheit eines Ein- oder Mehrkörpersystems bezeichnet. Dadurch nimmt die Anzahl der Freiheitsgrade eines Systems ab. Zwangsbedingungen führen zu Zwangskräften.
Systeme mit Zwangsbedingungen können besonders gut beschrieben werden durch
- die Lagrangesche Formulierung der klassischen Mechanik
- die Hamiltonsche Formulierung der klassischen Mechanik
- das D’Alembertsche Prinzip
- das Prinzip der virtuellen Leistung.
Unterscheidung
Bezüglich Integrabilität
Im Folgenden wird stets ein -Teilchensystem
in 3 Raumdimensionen
betrachtet. Ohne Zwangsbedingungen bräuchte man für den Ortsvektor jedes Teilchens
3 Raumkoordinaten, somit insgesamt
Raumkoordinaten, um das gesamte System zu beschreiben. Diese Koordinaten werden
fortlaufend durchnummeriert:
Holonome Zwangsbedingungen
Holonome
Zwangsbedingungen können als Gleichungen
zwischen den Koordinaten
des Systems formuliert werden (
:
Anzahl der holonomen Zwangsbedingungen):
Die
Koordinaten lassen sich mit
unabhängigen holonomen Zwangsbedingungen auf
unabhängige generalisierte
Koordinaten
reduzieren, die automatisch die Zwangsbedingungen erfüllen müssen:
Holonome Zwangsbedingungen sind mit dem vollständigen Differential einer Funktion darstellbar:
und somit integrierbar.
Denn notwendig für die Integrabilität ist, dass die Koeffizientenfunktionen
folgende Integrabilitätsbedingung
erfüllen:
was bei holonomen Bedingungen automatisch gegeben ist (
zweimal stetig
differenzierbar, siehe Satz
von Schwarz).
Das vollständige Differential läuft darauf hinaus, dass jede holonome Zwangsbedingung als eine Gleichung der Geschwindigkeiten darstellbar ist:
Anholonome Zwangsbedingungen
Nicht-holonome oder auch anholonome Zwangsbedingungen können nicht als Gleichungen zwischen den Koordinaten formuliert werden. Die generalisierten Koordinaten, die in solchen anholonomen Zwangsbedingungen erscheinen, sind i.A. nicht unabhängig voneinander variierbar.
Es handelt sich z.B. um Ungleichungen, wie Beschränkungen auf einen bestimmten Raumbereich:
oder um differentielle, nicht-integrable Zwangsbedingungen, wie Gleichungen
zwischen den Geschwindigkeiten
(Bsp. für
anholonome Zwangsbedingungen):
Nicht-integrabel heißt dabei, dass die Gleichung – anders als bei holonomen Zwangsbedingungen – nicht als vollständiges Differential einer Funktion darstellbar ist. Somit wird hier die Integrabilitätsbedingung von den Koeffizientenfunktionen nicht erfüllt:
Bezüglich Zeitabhängigkeit
Weiterhin werden Zwangsbedingungen bez. ihrer Zeitabhängigkeit unterschieden in:
- rheonom (fließend), wenn sie explizit von der Zeit abhängen.
- skleronom (starr), wenn sie nicht explizit von der Zeit abhängen.
Skleronome Zwangsbedingungen führen bei Anwendung des Lagrange'schen Formalismus in der Regel zu der Feststellung, dass das Potential nicht implizit von der Zeit abhängt. Ist das Potential nun auch nicht explizit zeitabhängig, so sind die Kräfte konservativ und die Energie ist erhalten. In diesem Fall ist die Hamiltonfunktion – die Legendre-Transformierte der Lagrange-Funktion – gleich der Gesamtenergie.
Dagegen lassen holonom-rheonome Zwangsbedingungen nicht direkt den Schluss auf eine Nicht-Erhaltung der Energie zu.
Beispiele
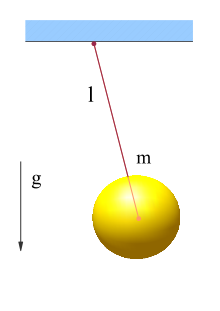
Das Pendel: holonom und skleronom
Der Stab eines ebenen Pendels
(d.h. nur 2 Raumdimensionen) soll stets die gleiche Länge
besitzen, muss also aufgrund des Satzes
von Pythagoras folgende Zwangsbedingung erfüllen (Anzahl der
Zwangsbedingungen:
):
Dabei bildet der Auslenkungswinkel
des Pendels aus der Senkrechten die generalisierte Koordinate. (Es gibt nur
eine, da
.)
Die Koordinaten
und
des Kugelmittelpunktes hängen von
ab (Annahmen:
nach rechts,
nach unten, Ursprung im Aufhängungspunkt):
Die generalisierte Koordinate erfüllt automatisch die Zwangsbedingung:
da allgemein gilt:
Dies ist ein Beispiel für eine holonome Zwangsbedingung und, da sie nicht
explizit von der Zeit abhängt (),
für eine skleronome Zwangsbedingung.
Vollständiges Differential der Zwangsbedingung:
Die Geschwindigkeits-Komponenten des Pendels lassen sich in der generalisierten Koordinate wie folgt ausdrücken (aufgrund der Zwangsbedingung kann sich die Kugel nur senkrecht zum Stab bewegen; Annahme hier: Bewegung nach rechts oben):
mit dem Betrag
der gesamten Geschwindigkeit.
Einsetzen der generalisierten Koordinate in die Zwangsbedingung in Form des vollständigen Differentials:
das somit ebenfalls automatisch erfüllt ist.
Teilchen in Kugel: anholonom und skleronom
Ein Teilchen sei in einer Kugel eingesperrt. Das bedeutet mathematisch, dass die Entfernung des Teilchens vom Mittelpunkt der Kugel (Koordinatenursprung) stets kleiner sein muss als der Radius R der Kugel:
Da diese Zwangsbedingung aus einer Ungleichung besteht, ist sie nichtholonom, und darüber hinaus, da sie nicht explizit von der Zeit abhängt, auch skleronom.
Literatur
- H. Goldstein: Klassische Mechanik. Wiley-VCH. ISBN 978-3527405893
- T. Fließbach: Mechanik – Lehrbuch zur Theoretischen Physik I. Spektrum Akademischer Verlag Heidelberg 2009. ISBN 978-3-8274-2148-7
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 07.10. 2022