Gradientenfeld

Ein Gradientenfeld ist ein Vektorfeld, das aus einem Skalarfeld durch Differentiation nach dem Ort abgeleitet wurde, bzw. – kürzer formuliert – der Gradient des Skalarfelds.

Zur besseren Abgrenzung zwischen dem Gradienten als mathematischem Operator und dem Resultat seiner Anwendung bezeichnen manche Autoren die Vektoren, aus denen sich Gradientenfelder zusammensetzen, auch als Gradientvektoren, andere dagegen mit Blick auf die Potentiale, aus denen sie sich herleiten, als Potentialvektoren.

Analog verwendet die überwiegende Zahl der Autoren den Begriff Potentialfeld nicht für das skalare Feld des Potentials selbst, sondern das sich aus ihm ableitende Gradientenfeld.

Definition und Eigenschaften

Ein Vektorfeld ${\vec F}\colon {\vec r}\mapsto {\vec F}({\vec r})$ heißt Gradientenfeld, wenn es ein Skalarfeld $\Phi \colon {\vec r}\mapsto \Phi ({\vec r})$ gibt, so dass

${\vec F}({\vec r})={\vec \nabla }\Phi ({\vec r})$

gilt. Dabei nennt man $\Phi$ das zu gehörige Skalarpotential oder einfach kurz das „Potential“ des Gradientenfelds ${\vec {F}}$ . Der Begriff darf jedoch nicht mit dem physikalischen Begriff des „Potentials“ verwechselt werden, mit dem die Fähigkeit eines konservativen Kraftfelds bezeichnet wird, einen dem Feld ausgesetzten Körper eine Arbeit verrichten zu lassen.

Physikalische Potentiale sind dabei stets auch Potentiale im Sinne der Mathematik, wenn damit die entsprechenden Ortsfunktionen (Felder) und nicht nur deren Funktionswerte gemeint sind. Jedoch ist umgekehrt nicht jedes mathematische Potential auch eines im o.g. physikalischen Sinn, etwa das der potentiellen Energie oder das Geschwindigkeitspotential.

Vektorfelder, die Gradienten eines Skalarfelds sind, werden in Anlehnung an den Begriff des „konservativen Kraftfelds“ oft auch als konservative Vektorfelder bezeichnet - ihnen allen gemeinsam sind dabei die folgenden drei einander äquivalenten Eigenschaften:

Wegunabhängigkeit des Kurvenintegrals: Der Wert des Kurvenintegrals entlang einer beliebigen Kurve innerhalb des Feldes ist nur von ihrem Anfangs- und Endpunkt abhängig, nicht dagegen von ihrer Länge.
Verschwinden des Ringintegrals für beliebige Randkurven :

$\oint _{S}\operatorname {grad}\,\Phi ({\vec r})\,{\mathrm d}{\vec r}=\oint _{S}{\vec F}({\vec r})\,{\mathrm d}{\vec r}=0$
Generelle Rotationsfreiheit bzw. Wirbelfreiheit des Feldes:

$\operatorname {rot}\,(\operatorname {grad}\,\Phi ({\vec r}))=\operatorname {rot}\,{\vec F}({\vec r})={\vec \nabla }\times {\vec F}({\vec r})={\vec 0}$

Beispiele

Beispiele von Potential- und Gradientenfeldern in der Physik
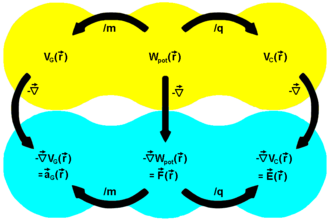
Skalarfelder (Potentialfelder) (gelb):
V_G - Gravitationspotential
W_pot - potentielle Energie
V_C - Coulomb-Potential
Vektorfelder (Gradientenfelder) (cyan):
a_G - Gravitationsbeschleunigung
F - Kraft
E - elektrische Feldstärke

Leitet man das Feld der potentiellen Energie $W_{\mathrm {pot} }({\vec {r}})$ , wie in der nebenstehenden Abb. gezeigt, nach dem Ort ${\vec {r}}$ ab, erhält man den Energiegradienten ${\vec {\nabla }}W_{\mathrm {pot} }({\vec {r}})$ , also ein Vektorfeld, dessen einzelne Vektoren dabei in die Richtung der jeweils stärksten Zunahme von $W_{\mathrm {pot} }({\vec {r}})$ an der Stelle ${\vec {r}}$ zeigen. Dem Prinzip des kleinsten Zwanges folgend, sind die diesem Gradienten entgegengesetzten Vektoren $-{\vec {\nabla }}W_{\mathrm {pot} }({\vec {r}})$ nichts anderes als die jeweils in Richtung des steilsten Gefälles von $W_{\mathrm {pot} }({\vec {r}})$ zeigenden „rücktreibenden“ Kräfte $F_{G}$ (Gravitationskraft) und $F_{C}$ (Coulombkraft)

${\vec {F}}_{G}=-{\vec {\nabla }}W_{\mathrm {pot} }({\vec {r}})\quad {\text{bzw.}}\quad {\vec {F}}_{C}=-{\vec {\nabla }}W_{\mathrm {pot} }({\vec {r}})$ .

Division des Energiegradienten ${\vec {\nabla }}W_{\mathrm {pot} }({\vec {r}})$ durch die Skalare m bzw. q liefert analog die Potentialgradienten ${\vec \nabla }V_{G}({\vec r})$ (Gravitationspotential) und ${\vec \nabla }V_{C}({\vec r})$ (Coulomb-Potential), deren einzelne Vektoren dabei abermals in Richtung der jeweils stärksten Zunahme des Potentials an der Stelle ${\vec {r}}$ zeigen. Die ihnen entgegengesetzten Vektoren $a_{G}$ und

${\vec a}_{G}=-{\vec \nabla }V_{{G}}({\vec r})\quad {\text{bzw.}}\quad {\vec E}=-{\vec \nabla }V_{{C}}({\vec r})$

heißen Gravitationsbeschleunigung bzw. elektrische Feldstärke.

Vorzeichen

Handelt es sich bei dem zugrundeliegenden Skalarpotential auch um ein Potential im physikalischen Sinne (s.o.), beschreibt es also ein tatsächliches physikalisches Arbeitsvermögen, wird das sich aus ihm ergebende Gradientenfeld, wie gerade begründet, stets mit einem (der Zunahme des Betrags von ${\vec {r}}$ entgegengesetzten) negativem Vorzeichen geschrieben. Bei Skalarfeldern dagegen, die sich nur mathematisch wie Potentiale verhalten, etwa dem Strömungs- oder Geschwindigkeitspotential, das damit auch keine potentielle Energie repräsentiert, ist das Vorzeichen seines Gradienten undefiniert und wird für gewöhnlich positiv gewählt:

Kraft - Potentielle Energie: $\quad {\vec {F}}({\vec {r}})=-{\vec {\nabla }}W_{\mathrm {pot} }({\vec {r}})$

Elektrische Feldstärke - Coulomb-Potential: ${\vec E}({\vec r})=-{\vec \nabla }V_{{C}}({\vec r})$

Gravitationsbeschleunigung - Gravitationspotential: ${\vec a}_{G}({\vec r})=-{\vec \nabla }V_{{G}}({\vec r})$

aber

Geschwindigkeit - Geschwindigkeitspotential: ${\vec v}({\vec r})=+{\vec \nabla }\Phi ({\vec r})$

Integrabilitätsbedingung

Ist $U\subseteq \mathbb {R} ^{n}$ eine offene und einfach zusammenhängende (zum Beispiel sternförmige) Menge und ${\vec F}\colon U\to {\mathbb {R}}^{n}$ stetig differenzierbar, so ist ${\vec {F}}$ genau dann ein Gradientenfeld, wenn die Integrabilitätsbedingungen

${\frac {\partial F_{i}}{\partial x_{j}}}={\frac {\partial F_{j}}{\partial x_{i}}}$ für alle $i,j\in \{1,\dots ,n\}$

auf erfüllt ist. Die Aussage erhält man als Spezialfall aus dem Poincaré-Lemma.

Im Zwei- und Dreidimensionalen lauten die Integrabilitätsbedingungen:

Für $\mathbb {R} ^{2}$ : ${\frac {\partial F_{1}}{\partial x_{2}}}={\frac {\partial F_{2}}{\partial x_{1}}}$
Für $\mathbb {R} ^{3}$ : ${\frac {\partial F_{1}}{\partial x_{2}}}={\frac {\partial F_{2}}{\partial x_{1}}},\ {\frac {\partial F_{1}}{\partial x_{3}}}={\frac {\partial F_{3}}{\partial x_{1}}}{\text{ und }}{\frac {\partial F_{2}}{\partial x_{3}}}={\frac {\partial F_{3}}{\partial x_{2}}}$

Äquivalent dazu ist in beiden Fällen die Bedingung $\operatorname {rot}\,{\vec F}={\vec 0}$ , also dass die Rotation verschwindet.

Auf Gebieten, die nicht einfach zusammenhängend sind, sind diese Integrabilitätsbedingungen zwar notwendig, aber im Allgemeinen nicht hinreichend.

Basierend auf einem Artikel in:

Wikipedia.de