
Konservative Kraft
Konservative Kräfte sind in der Physik Kräfte, die längs eines beliebigen geschlossenen Weges (Rundweg) keine Arbeit verrichten. An Teilstrecken aufgewendete Energie wird an anderen Strecken wieder zurückgewonnen. Das heißt, die kinetische Energie eines Probekörpers bleibt ihm am Ende erhalten.
Beispiele konservativer Kräfte sind zum einen solche, die wie die Gravitationskraft oder Coulombkraft des elektrischen Feldes durch konservative Kraftfelder (s. u.) vermittelt werden, zum anderen aber auch Kräfte wie z. B. Federkräfte, die nicht durch Kraftfelder im eigentlichen Sinn vermittelt werden. Da einer konservativen Kraft ein Potential zugeordnet werden kann, kann die Kraft nur vom Ort abhängen und nicht wie zum Beispiel dissipative Kräfte von der Geschwindigkeit.
Bekanntestes Beispiel einer durch ein Kraftfeld vermittelten konservativen
Kraft ist die Erdanziehungskraft. Die Kraft
ist gerade die negative Ableitung der potentiellen Energie z. B. als Näherung
nahe der Erdoberfläche
nach der Höhe h. Egal auf welchem Weg man von einem Punkt auf Höhe
zu einem Punkt auf Höhe
gelangt, ist dabei immer dieselbe Arbeit
aufzubringen. Die potentielle Energie bezieht sich dabei allerdings immer noch
auf eine Probemasse m (oder Probeladung q im Fall des elektrischen
Feldes), während das von der Probe unabhängige Skalarfeld
(bzw.
im Fall des elektrischen Feldes) das physikalische Potential an der
betreffenden Stelle genannt wird und als solches eine äquivalente Darstellung
des zugrundeliegenden Vektorfelds ist.
Das Gegenteil konservativer Kräfte sind nicht-konservative Kräfte, also solche, die längs eines in sich geschlossenen Weges Arbeit verrichten, und zwar umso mehr, je länger der dabei zurückgelegte Weg ist. Beispiele derartiger nicht-konservativer Kräfte sind zum einen Kräfte in nicht-konservativen Kraftfeldern wie etwa (magnetischen) Wirbelfeldern, zum anderen sogenannte dissipative Kräfte (von lateinisch dissipare = zerstreuen), z. B. Reibungskräfte.
Die meisten physikalischen Systeme sind, da ihnen stets Energie durch Reibung und/oder nicht-konservative Kraftfelder (z. B. Wirbelfelder) verloren geht, nicht-konservativ. Erweitert man dagegen die Perspektive, indem man beispielsweise bei Betrachtung der Energieverluste durch Reibung auch die Energieinhalte angekoppelter Wärmereservoirs mit berücksichtigt, bleibt die Energie am Ende doch immer in irgendeiner Form erhalten.
Konservative Kraftfelder
Konservative Kraftfelder sind dem zuvor Gesagten folgend solche, in denen ein Probekörper beim Durchlaufen eines in sich geschlossenen Weges weder Energie gewinnt noch verliert.
Es lässt sich zeigen, dass die nachstehenden vier Charakteristika eines
konservativen Kraftfelds
einander äquivalent sind:
- 1. Die Arbeit entlang jeder beliebigen geschlossenen Kurve
innerhalb des Feldes ist gleich Null, also
.
- 2. Die Arbeit
entlang eines beliebigen Weges
durch das Kraftfeld ist nur vom Anfangs- und Endpunkt des Weges, nicht aber von seinem Verlauf abhängig.
- 3. Es existiert ein
, welches das zugehörige Potential des Kraftfelds genannt wird, so dass sich die Kraft
auch in der Form
beschreiben lässt, d. h. als Gradientenfeld, mit
als dem Nabla-Operator,
als dem Gradienten des Potentials und der Ladung oder Kopplungsstärke
, die im Fall des elektrischen Felds die elektrische Ladung q des Probekörpers, im Fall des Gravitationsfelds seine Masse m ist.
- 4. Das Feld ist auf einem einfach
zusammenhängenden Gebiet definiert und erfüllt dort die Integrabilitätsbedingung
. Dies bedeutet, dass die Rotation verschwindet, also
bzw.
ist.
Analog zum eben Gesagten werden in der Mathematik ganz allgemein Vektorfelder, die sich als Gradienten skalarer Felder beschreiben lassen, als konservativ bezeichnet, zusammengesetzt aus Potentialvektoren, denen auf Seiten der skalaren Ausgangsfelder die zugehörigen Potentiale gegenüberstehen.
Potentiale und Potentialfelder
Der Begriff des Potentials wird in der Physik und Mathematik zum Teil unterschiedlich gebraucht.
So bezeichnet das Potential
in der Mathematik ganz allgemein eine Klasse skalarer Ortsfunktionen bzw. Skalarfelder mit bestimmten
mathematischen Eigenschaften, während es in der Physik nur den Quotienten der potentiellen
Energie
eines Körpers an der Stelle
und seiner elektrischen Ladung q bzw. Masse m definiert:
Ein Potential
im physikalischen Sinn
ist dabei stets auch eines im mathematischen Sinn, jedoch nicht umgekehrt: So
sind sowohl das Gravitations-
und Coulomb-Potential
wie auch die potentielle Energie
in einem konservativen Kraftfeld ihrer mathematischen Natur nach Potentiale, im
physikalischen Sinn jedoch nur die beiden erstgenannten.
Ähnlich verhält es sich mit der Terminologie bei den Gradienten von
Potentialen, also den aus den jeweiligen Skalarfeldern
abgeleiteten Vektorfeldern
also Beschleunigungsfeldern
bzw
:
Dennoch werden häufig auch die Kraftfelder
bzw
als „Potentialfelder“
bezeichnet.
Beispiel
Der Gradient der potentiellen
Energie
an der Stelle
liefert die an dieser Stelle wirkende und dem Prinzip des
kleinsten Zwanges folgend stets in Richtung abnehmender potentieller Energie
zeigende „rücktreibende“ Kraft
:
In der Nähe der Erdoberfläche ist die potentielle Energie
einer Masse
in Höhe
über dem Boden unter Annahme einer für kleinen Höhenänderungen annähernd
konstanten Erdbeschleunigung
gleich
.
Ersetzt man, da es sich beim Gravitationsfeld der Erde um ein zumindest lokal
radiales Feld handelt, den Ortsvektor
durch die Höhe
und den Gradienten durch die Ableitung nach
,
ergibt sich damit für die Schwerkraft die Formel:
Wie dem Vorzeichen
des Resultats anzusehen, ist die Kraft
der Richtung zunehmender Höhe entgegengesetzt.
Lokale Konservativität

Beim letzten der obengenannten vier Charakteristika konservativer Kraftfelder
ist insbesondere auf das Kriterium des „einfach zusammenhängenden Gebiets“, also
darauf zu achten, dass das Gebiet, anschaulich gesprochen, keine „Löcher“ oder
ähnliche Definitionslücken enthält. Nicht „einfach zusammenhängend“ in diesem
Sinn ist beispielsweise das Gebiet um einen stromdurchflossenen Leiter, dessen
Magnetfeld zwar außerhalb des Leiters wie nachstehend definiert ist, für
die z-Achse (0|0|z) selbst jedoch weder
noch seine Ableitung existieren:
So gilt zwar außerhalb des Leiters .
Dennoch verschwindet ein Ringintegral um die z-Achse nicht. Integriert
man zum Beispiel entlang des Einheitskreises, der durch
mit
parametrisiert wird, so erhält man als Wegintegral
Obwohl die Rotation
mit Ausnahme der Definitionslücke
an der z-Achse überall verschwindet, ist das B-Feld dadurch nicht
durchgehend konservativ. Da die Energie dennoch auf allen Pfaden erhalten
bleibt, die die z-Achse nicht umschließen, spricht man hier einschränkend
von lokaler Konservativität.
Beweis der Äquivalenz der Kriterien
Wie anfangs bereits festgestellt, sind die vier Definitionen für ein konservatives Kraftfeld miteinander gleichbedeutend. Das erste Kriterium ist gerade die Definition einer konservativen Kraft aus der Einleitung, die anderen folgen daraus.
1. Davon ausgehend, dass die Arbeit entlang eines geschlossenen Pfades
verschwindet, kann zunächst die Korrektheit des zweiten Kriteriums gezeigt
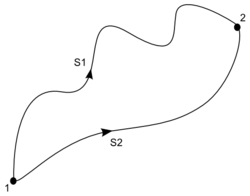
werden. Man betrachte dazu zwei Wege
und
zwischen den Punkten 1 und 2 in einem konservativen Kraftfeld wie im Bild
rechts:
Verläuft
von Punkt 1 über Weg
zum Punkt 2, dann über den Weg
zurück zum Punkt 1, so ergibt sich das Ringintegral über diesen
Weg damit zu
Mit
ist das dann und genau dann null, wenn
was gerade der Wegunabhängigkeit und damit der zweiten Definition für ein konservatives Kraftfeld entspricht.
2. Wenn ,
so ist
, unabhängig vom Weg S.
3. Wenn ,
so gilt für die Rotation
,
wobei der letzte Schritt wegen der Vertauschbarkeit der partiellen Ableitungen gemäß dem Satz von Schwarz zustande kam.
4. Nach dem Satz von Stokes gilt für eine Fläche A, die von einer geschlossenen Kurve C umschlossen wird
.
Dieses Integral verschwindet für alle Kurven C dann und genau dann,
wenn
ist.
Energieerhaltung
In der klassischen Mechanik gilt für die kinetische Energie
,
wobei
die Geschwindigkeit
ist.
Mit dem zweiten Newtonschen Axiom
für konstante Massen
kann die Energie geschrieben werden.
.
Dann gilt für den Weg von Punkt 1 zum Punkt 2 das Wegintegral
.
Für die rechte Seite dieser Gleichung gilt
.
Das bedeutet, dass die gesamte Arbeit, die bei der Bewegung aufgebracht wird, der Änderung der kinetischen Energie entspricht. Für die linke Seite gilt hingegen unter Verwendung der Eigenschaften konservativer Kräfte
und damit
bzw.
was gerade dem Energieerhaltungssatz entspricht. Die Eigenschaft der Energieerhaltung ist auch der Grund, weshalb konservative Kraftfelder ihren Namen erhielten – die Energie ist konserviert.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 13.09. 2021