
Skalarfeld
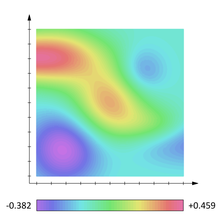
In der mehrdimensionalen Analysis, der Vektorrechnung und der Differentialgeometrie ist ein skalares Feld (kurz Skalarfeld) eine Funktion, die jedem Punkt eines Raumes eine reelle Zahl (Skalar) zuordnet, z.B. eine Temperatur.
Skalarfelder sind von großer Bedeutung in der Feldbeschreibung der Physik und in der mehrdimensionalen Vektoranalysis.
Definition
Ein Skalarfeld
bildet jeden Punkt
einer Mannigfaltigkeit
auf einen Skalar
ab.
Man unterscheidet dabei zwischen reellwertigen Skalarfeldern
und komplexwertigen Skalarfeldern
.
Man spricht von einem stationären Skalarfeld, wenn die Funktionswerte nur vom Ort abhängen. Hängen sie auch von der Zeit ab, handelt es sich um ein instationäres Skalarfeld.
Beispiele
Beispiele für Skalarfelder in der Physik sind der Luftdruck, die Temperatur, Dichte oder allgemein Potentiale (auch als Skalarpotentiale bezeichnet).
Operationen
Wichtige Operationen im Zusammenhang mit Skalarfeldern sind:
- Gradient eines Skalarfeldes, der ein Vektorfeld ist.
- Richtungsableitung eines Skalarfeldes.
Einordnung
Im Gegensatz zum Skalarfeld ordnet ein Vektorfeld jedem Punkt einen Vektor zu. Ein Skalarfeld ist das einfachste Tensorfeld.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 25.11. 2020