Vektorfeld

Darstellung eines Vektorfeldes anhand ausgewählter Punkte. Die Vektoren sind als Pfeile dargestellt, welche Richtung und Betrag (Pfeillänge) wiedergeben

3-dimensionales Vektorfeld (-y,z,x)

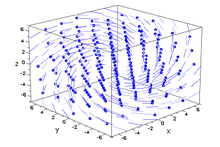
In der mehrdimensionalen Analysis und der Differentialgeometrie ist ein Vektorfeld eine Funktion, die jedem Punkt eines Raumes einen Vektor zuordnet. Das duale Konzept zu einem Vektorfeld ist eine Funktion, die jedem Punkt eine Linearform zuordnet, eine solche Abbildung wird pfaffsche Form genannt.

Stetige Vektorfelder sind von großer Bedeutung in der physikalischen Feldtheorie, zum Beispiel um die Geschwindigkeit und Richtung eines Teilchens einer bewegten Flüssigkeit anzugeben, oder um die Stärke und Richtung einer Kraft, wie der magnetischen oder der Schwerkraft, zu beschreiben. Die Feldgrößen dieser Vektorfelder lassen sich durch Feldlinien veranschaulichen.

Vektorfelder im euklidischen Raum

Definition

Unter einem Vektorfeld auf einer Menge $\Omega \subset \mathbb{R}^n$ versteht man eine Abbildung, die jedem Punkt $x\in \Omega$ einen Vektor $v(x)\in \mathbb{R} ^{n}$ zuordnet. Anschaulich wird also an jedem Punkt der Menge $\Omega$ ein „Pfeil angebracht“. Meist wird stillschweigend vorausgesetzt, dass das Vektorfeld glatt, also eine $C^{\infty }$ -Abbildung ist. Ist eine -mal differenzierbare Abbildung $v\colon \Omega \to \mathbb {R} ^{n}$ , so spricht man von einem $C^{k}$ -Vektorfeld.

Beispiele

Gradientenfeld: Ist $f\colon \Omega \rightarrow \mathbb{R}$ eine differenzierbare Funktion auf einer offenen Menge $\Omega \subset \mathbb {R} ^{n}$ , so wird das Gradientenfeld $\operatorname {grad}f\colon \Omega \rightarrow \mathbb{R} ^{n}$ von definiert durch die Zuordnung

$x \mapsto \operatorname{grad} f(x) = \left(\frac{\partial f}{\partial x_1}(x), \dotsc, \frac{\partial f}{\partial x_n}(x)\right)$ .

Oft schreibt man es mit dem Nabla-Symbol: $\operatorname {grad}f=\nabla f$ . Ist ein Vektorfeld das Gradientenfeld einer Funktion , das heißt $v=\nabla f$ , so bezeichnet man als Potential. Man sagt auch besitzt ein Potential.

Beispiele von Gradientenfeldern sind das von einer Punktquelle nach allen Seiten gleichmäßig fließende Feld einer Strömung und das elektrische Feld um eine Punktladung.

Zentralfelder: Sei ein Intervall, welches die Null enthält, und $K(I)=\{x\in \mathbb{R} ^{n}:\|x\|\in I\}\subset \mathbb{R} ^{n}$ eine Kugelschale. Zentralfelder auf der Kugelschale sind definiert durch

$v(x)=a(\|x\|)\cdot x$ mit $a\colon I \rightarrow \R$ .

In $\mathbb{R} ^{3}\backslash \{0\}$ ist das Gravitationsfeld $v(x)=-{\frac {x}{\|x\|^{3}}}$ ein solches Zentralfeld.
Weitere Beispiele sind im $\mathbb {R} ^{3}$ die mathematisch diffizileren sogenannten „Wirbelfelder“. Sie lassen sich als Rotation eines Vektorpotentials $\mathbf {A}$ beschreiben, nach der Formel ${\mathbf v}({\mathbf r})={\mathbf {rot\,\,}}{\mathbf A}$ (s.u.).

Prägnantes Beispiel eines Wirbelfeldes ist das in Kreislinien um den Ausfluss einer „Badewanne“ herumwirbelnde Strömungsfeld, oder das Magnetfeld um einen stromdurchflossenen Draht.

Quellenfreie und wirbelfreie Vektorfelder; Zerlegungssatz

Ein mindestens zweimal stetig differenzierbares Vektorfeld $\mathbf v(\mathbf r)$ im $\mathbb {R} ^{3}$ heißt quellenfrei (beziehungsweise wirbelfrei), wenn seine Quellendichte (Divergenz) beziehungsweise Wirbeldichte (Rotation) dort überall Null ist. Unter der weiteren Voraussetzung, dass die Komponenten von $\mathbf v$ im Unendlichen hinreichend rasch verschwinden, gilt der sogenannte Zerlegungssatz: Jedes Vektorfeld $\mathbf v(\mathbf r)$ ist eindeutig durch seine Quellen bzw. Wirbel bestimmt, und zwar gilt die folgende Zerlegung in einen wirbelfreien beziehungsweise quellenfreien Anteil:

$\mathbf v(\mathbf r)\equiv \mathbf{-grad_{\mathbf r}\,\,} \int_{\mathbb R^3\,}\,d^3\mathbf r'\,\frac{\mathrm{{div'}\,\,}\mathbf v(\mathbf r')}{4\pi|\mathbf r -\mathbf r'|}+ \mathbf{rot_{\mathbf r}\,\,} \int_{\mathbb R^3\,}\,d^3\mathbf r'\,\,\frac{{\mathbf{rot'\,\,}}\mathbf v(\mathbf r')}{4\pi|\mathbf r -\mathbf r'|}$ .

Dies entspricht der Zerlegung eines statischen elektromagnetischen Feldes in den elektrischen beziehungsweise magnetischen Anteil (siehe Elektrodynamik)^[1]. Es sind also genau die Gradientenfelder (d.h. die „elektrischen Feldkomponenten“) wirbelfrei bzw. genau die Wirbelfelder (d.h. die „magnetischen Feldkomponenten“) quellenfrei. Dabei sind ${\mathbf {grad\,\,}}\phi ({\mathbf r}):=\nabla \phi \,,$ ${\mathrm {div\,\,}}{\mathbf v}:=\nabla \cdot {\mathbf v}$ und ${\mathbf {rot\,\,}}{\mathbf v}:=\nabla \times {\mathbf v}$ die bekannten, mit dem Nabla-Operator ( $\nabla$ ) der Vektoranalysis gebildeten Operationen.

Vektorfelder auf Mannigfaltigkeiten

Definition

Sei eine differenzierbare Mannigfaltigkeit. Ein Vektorfeld ist ein (glatter) Schnitt im Tangentialbündel .

Ausführlicher heißt das, ein Vektorfeld ist eine Abbildung , so dass $v\colon M\to TM$ mit $\pi \circ v=\operatorname {id}_{M}$ gilt. Es wird also jedem $x\in M$ ein Vektor $v(x)\in T_{x}M$ zugeordnet. Die Abbildung $\pi$ ist die natürliche Projektion $\pi \colon TM\to M$ mit $(p,v)\mapsto p$ .

Anmerkungen

Diese Definition verallgemeinert die Vektorfelder im euklidischen Raum. Es gilt nämlich $\mathbb{R} ^{n}\cong T_{p}\mathbb{R} ^{n}$ und $T\mathbb{R} ^{n}\cong \mathbb{R} ^{n}\times \mathbb{R} ^{n}$ .

Im Gegensatz zu Vektorfeldern wird durch ein Skalarfeld jedem Punkt einer Mannigfaltigkeit ein Skalar zugeordnet.

Vektorfelder sind gerade die kontravarianten Tensorfelder erster Stufe.

Anwendungen

Vektor- und Kraftfelder haben außer in Physik und Chemie auch große Bedeutung in zahlreichen Fachgebieten der Technik: Elektrotechnik, Geodäsie, Mechanik, Atomphysik, Angewandte Geophysik.

Literatur

Konrad Königsberger: Analysis 2. 5. korrigierte Auflage. Springer, Berlin u.a. 2004, ISBN 3-540-20389-3.

Basierend auf einem Artikel in:

Wikipedia.de