Sprungklammer

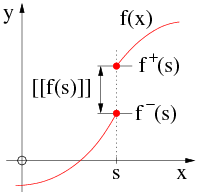
Unstetige Funktion f(x) mit Sprungstelle bei x=s und Sprunghöhe [[f(s)]]

Die Sprungklammer [[...]] ist eine vereinfachende Schreibweise für die Sprunghöhe einer Funktion an einer Unstetigkeitsstelle, siehe Bild.

In der Kontinuumsmechanik kommen solche Sprungstellen beispielsweise vor

an Krafteinleitungsstellen, wo Kräfte flächig eingeleitet werden und am Rand der Einleitungsstelle schlagartig auf null zurückgehen,
an Materialgrenzen, wo die Dichte einen diskontinuierlichen Verlauf hat, oder
in Stoßwellen, wo auch die Geschwindigkeit einen Sprung machen kann.

Diese Situationen sind durchaus häufig und teilweise allgegenwärtig, so dass sie nicht ignoriert werden können. Die resultierenden Terme in den Gleichungen, beispielsweise dem Reynolds’schen Transportsatz, lassen sich mit der Sprungklammer kurz und lesbar schreiben.

Für die Definition wird eine reellwertige Funktion $f\colon \R\to\R$ betrachtet, die an der Stelle x=s eine Unstetigkeitsstelle besitze. Bei Annäherung von unten sei der linksseitige Grenzwert $\lim _{x\to s-}f(x)=f^{-}(s)$ und von oben der rechtsseitige Grenzwert $\lim _{x\to s+}f(x)=f^{+}(s)$ berechenbar. Dann ist die Sprungklammer eine Kurzschreibweise für die Differenz dieser Grenzwerte an der Sprungstelle:

$[[f(s)]]:=\lim _{x\to s+}f(x)-\lim _{x\to s-}f(x)=f^{+}(s)-f^{-}(s)\,.$

Die Funktionen können die Komponenten von Vektor- oder Tensorfeldern sein, weswegen sich die Klammer auch auf vektorielle oder tensorielle Argumente verallgemeinern lässt.

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de