Verschiebungsmethode

Die Verschiebungsmethode ist die Standardformulierung der Finite-Elemente-Methode (FEM), bei der die Verschiebungen der Körperpunkte die primären Unbekannten sind. In der Festkörpermechanik beinhalten die Verschiebungen die Wege, die die Körperpunkte mit der Zeit zurücklegen und damit die Translation, Rotation und möglicherweise Verformung eines Festkörpers. Die erste Anwendung der FEM war die lineare Behandlung von Festkörpern und Strukturen (bestehend aus Stäben, Balken oder Schale) und davon ausgehend hat die FEM ihre Anstöße erhalten.

Eine der Verschiebungsmethode zugrunde liegende Gleichung ist das Prinzip von d’Alembert in der Lagrange’schen Fassung. Mit diesem Prinzip können sowohl lineare Probleme, wie die Frage nach Eigenschwingungen, als auch hoch nichtlineare Probleme, wie Crashtests, analysiert werden. Wegen ihrer Einsetzbarkeit in den meisten Problemstellungen werden in der Standardformulierung isoparametrische Elemente verwendet. Auch die Galerkin-Methode wird verwendet.

Die Verschiebungsmethode ist in allen gängigen Finite-Elemente-Programmen verfügbar, mit denen Probleme der Festkörpermechanik berechnet werden können, wobei sich die Programme in den verwendeten Dehnungsmaßen, implementierten Nichtlinearitäten, Materialmodellen, Zeitintegrationsverfahren und/oder numerischen Umsetzungen unterscheiden können.

Matrizengleichungen

Das Prinzip von d’Alembert in der Lagrange’schen Fassung ist eine zur Impulsbilanz äquivalente Aussage und lautet

$\int _{V}\delta {\vec {u}}\cdot \rho _{0}{\ddot {\vec {u}}}\,{\text{d}}V+\int _{V}{\tilde {\mathbf {T} }}:\delta \mathbf {E} \,{\text{d}}V=\int _{{A}^{\sigma }}\delta {\vec {u}}\cdot {\vec {t}}_{0}\,{\text{d}}A+\int _{V}\delta {\vec {u}}\cdot \rho _{0}{\vec {k}}_{0}\,{\text{d}}V\quad \forall \;\delta {\vec {u}}\in {\mathcal {V}}\,.$

Der erste Term ist die über das Volumen V des Körpers summierte virtuelle Arbeit der Impulsänderung $\rho_0\ddot{\vec{u}}$ an den virtuellen Verschiebungen $\delta\vec{u}\,.$ Der Faktor $\rho _{0}$ ist die Dichte und ${\ddot {{\vec {u}}}}$ die Beschleunigung des materiellen Punktes. Im zweiten Term wird die vom Spannungstensor ${\tilde {{\mathbf {T}}}}$ am virtuellen Verzerrungstensor $\delta\mathbf{E}$ geleistete virtuelle Deformationsarbeit, die mit dem Frobenius-Skalarprodukt „:“ der Tensoren gebildet wird, über das Volumen V des Körpers summiert. Auf der rechten Seite steht die Arbeit der äußeren Kräfte (oberflächen- und volumenverteilt) an den virtuellen Verschiebungen. Die Menge ${\mathcal {V}}$ enthält alle zulässigen virtuellen Verschiebungen, die verschwinden woimmer Verschiebungsrandbedingungen vorgegeben sind. Die Fläche ${A}^{\sigma }$ ist derjenige Teil der Oberfläche des Körpers, auf der keine Verschiebungsrandbedingungen vorliegen.

Wenn die Gleichung oben tatsächlich für alle erlaubten virtuellen Verschiebungen erfüllt ist, dann sind die Verschiebungen sowie die daraus resultierenden Verzerrungen und Spannungen im Einklang mit der Impulsbilanz. Die vorausgesetzte Symmetrie des Spannungstensors bewirkt zusätzlich die Erfüllung der Drehimpulsbilanz.

Überführung des Prinzips in eine Matrizengleichung

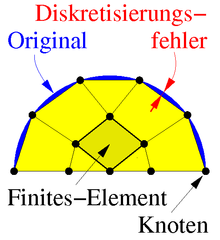
Halbkreis (blau) und sein FE-Modell (gelb).

Der interessierende Körper wird vorbereitend in Teilkörper, die Finiten-Elemente, unterteilt, siehe Bild. Damit die Elemente den Körper lückenlos und überschneidungsfrei aufbauen, müssen benachbarte Elemente kompatibel sein. Auf den Begrenzungsflächen oder auch im Inneren der Elemente liegen Knoten genannte Punkte, denen globale Koordinaten zur geometrischen Beschreibung des Körpers und Verschiebungen als Knotenvariable zur Beschreibung der Bewegung zugeteilt werden.

Anhand eines Elementes wird die Überführung der Tensorgleichung des Prinzips in eine Matrizengleichung vollzogen:

Die Elementverschiebungen werden mit einem rein zeitabhängigen Lösungsvektor ${\hat {u}}$ der Länge m mit Knotenverschiebungen und einer rein ortsabhängigen 3×m Formfunktionsmatrix N dargestellt:

${\vec {u}}=N{\hat {u}}\,.$

Damit lauten die Elementbeschleunigungen ${\ddot {\vec {u}}}=N{\hat {\ddot {u}}}\,.$ Die Formfunktionen sind die Ansatzfunktionen für die Lösung und durch die Beschränkung auf eine endliche Anzahl von ihnen ergibt sich der – in Abwesenheit einer analytischen Lösung unvermeidliche – Diskretisierungsfehler.

In der Galerkin-Methode werden die virtuellen Verschiebungen genauso behandelt wie die Punktverschiebungen:

$\delta {\vec {u}}=N\delta {\hat {u}}\,.$

Der Spannungstensor wird mittels Voigt’scher Notation als Spaltenvektor geschrieben:

${\hat {T}}={\begin{pmatrix}{\tilde {T}}_{xx}&{\tilde {T}}_{yy}&{\tilde {T}}_{zz}&{\tilde {T}}_{xy}&{\tilde {T}}_{yz}&{\tilde {T}}_{xz}\end{pmatrix}}^{\top }\,.$

Das Superskript $(\cdot )^{\top }$ bezeichnet die Transposition.

In gleicher Weise werden die virtuellen Verzerrungen in einen Vektor eingetragen:

$\delta {\hat {E}}={\begin{pmatrix}\delta E_{xx}&\delta E_{yy}&\delta E_{zz}&2\delta E_{xy}&2\delta E_{yz}&2\delta E_{xz}\end{pmatrix}}^{\top }\,.$

Der Faktor zwei an der vierten bis sechsten Position stellt sicher, dass das Skalarprodukt mit dem Matrixprodukt übereinstimmt ${\tilde {\mathbf {T} }}:\delta \mathbf {E} =\delta {\hat {E}}^{\top }{\hat {T}}\,.$ Außerdem entspricht die doppelte Schubverzerrung der Gleitung γ, so dass die Komponenten eine anschauliche Interpretation besitzen.

Die differentiellen virtuellen Verzerrungen sind linear in den virtuellen Knotenverschiebungen:

$\delta {\hat {E}}=B\delta {\hat {u}}$

mit der 6×m Verzerrungsverschiebungsmatrix B.

Diese Definitionen, die im Abschnitt #Elementmatrizen an den Integrationspunkten unten ausgeführt werden, werden in das Prinzip eingetragen:

${\begin{aligned}\int _{V}\delta {\hat {u}}^{\top }N^{\top }\rho _{0}N{\hat {\ddot {u}}}\,{\text{d}}V+\int _{V}\delta {\hat {E}}^{\top }{\hat {T}}\,{\text{d}}V=\int _{{A}^{\sigma }}\delta {\hat {u}}^{\top }N^{\top }{\vec {t}}_{0}\,{\text{d}}A+\int _{V}\delta {\hat {u}}^{\top }N^{\top }\rho _{0}{\vec {k}}_{0}\,{\text{d}}V&\quad \forall \;\delta {\hat {u}}\in V^{m}\\\rightarrow \delta {\hat {u}}^{\top }{\Biggl [}\underbrace {\int _{V}N^{\top }\rho _{0}N\,{\text{d}}V} _{M}{\hat {\ddot {u}}}+\underbrace {\int _{V}B^{\top }{\hat {T}}\,{\text{d}}V} _{\hat {r}}-\underbrace {\left(\int _{{A}^{\sigma }}N^{\top }{\vec {t}}_{0}\,{\text{d}}A+\int _{V}N^{\top }\rho _{0}{\vec {k}}_{0}\,{\text{d}}V\right)} _{\hat {f}}{\Biggr ]}=0&\quad \forall \;\delta {\hat {u}}\in V^{m}\,.\end{aligned}}$

Die Menge V^m enthält alle zulässigen virtuellen Verschiebungsvektoren der Dimension m×1. Die Knotenvariablen können aus den Integralen herausgezogen werden, weil die Ortsabhängigkeit allein bei den Formfunktionen liegt. So entsteht die Prinzipgleichung:

$\delta {\hat {u}}^{\top }[M{\hat {\ddot {u}}}+{\hat {r}}-{\hat {f}}]=0\quad \forall \;\delta {\hat {u}}\in V^{m}$		(PvdA)

Die m×m Matrix M ist die konstante Massenmatrix, der m×1 Vektor $\hat r$ enthält Knotenreaktionen aufgrund von Elementspannungen und ${\hat f}$ ist der gleich große Knotenkraftvektor, der die von außen angreifenden Kräfte repräsentiert.

Diese Gleichung wurde für ein Finites-Element aufgestellt, was statthaft ist, weil das Prinzip für jeden Körper und jeden seiner Teilkörper gilt. Beim Übergang vom Finiten-Element zum ganzen Körper werden die Elementmatrizen in einem Assemblierungsschritt in globalen Matrizen aufsummiert. Das globale System unterliegt auch der Prinzipgleichung (PvdA), nur die Matrizen und Vektoren sind größer.

Partitionierung des globalen Systems

Die Menge V^m enthält alle zulässigen virtuellen Verschiebungsvektoren der Dimension m×1. Zulässig ist ein virtueller Verschiebungsvektor, wenn seine Komponenten verschwinden, wo im Lösungsvektor Randbedingungen vorgegeben sind. Die Komponenten des Lösungsvektors, die an Verschiebungsrandbedingungen gebunden sind, werden an das Ende des Lösungsvektors verlegt:

${\hat {u}}={\begin{pmatrix}{\hat {u}}_{u}\\{\hat {u}}_{b}\end{pmatrix}}\quad \rightarrow \quad \delta {\hat {u}}={\begin{pmatrix}\delta {\hat {u}}_{u}\\{\hat {0}}\end{pmatrix}}\,,\quad {\hat {f}}={\begin{pmatrix}{\hat {f}}_{u}\\{\hat {0}}\end{pmatrix}}$

Der Vektor $\hat{u}_u$ enthält die gesuchten unbekannten Knotenverschiebungen und ${\hat {u}}_{b},\,{\hat {f}}_{u}$ sind in Randbedingungen vorgegeben. Im Vektor der äußeren Kräfte $\hat{f}$ besteht der untere Teil aus Nullen, weil an Orten, wo Verschiebungsrandbedingungen vorliegen, keine Kräfte vorgegeben werden können. Die Massenmatrix wird ebenfalls partitioniert:

$M=\begin{pmatrix}M_{uu} & M_{ub}\\M_{bu}& M_{bb}\end{pmatrix}\,.$

Damit entsteht aus der Gleichung (PvdA):

${\begin{aligned}{\begin{pmatrix}\delta {\hat {u}}_{u}^{\top }&{\hat {0}}^{\top }\end{pmatrix}}\left[{\begin{pmatrix}M_{uu}&M_{ub}\\M_{bu}&M_{bb}\end{pmatrix}}{\begin{pmatrix}{\hat {\ddot {u}}}_{u}\\{\hat {\ddot {u}}}_{b}\end{pmatrix}}+{\begin{pmatrix}{\hat {r}}_{u}\\{\hat {r}}_{b}\end{pmatrix}}-{\begin{pmatrix}{\hat {f}}_{u}\\{\hat {0}}\end{pmatrix}}\right]=&\\\delta {\hat {u}}_{u}^{\top }\left(M_{uu}{\hat {\ddot {u}}}_{u}+M_{ub}{\hat {\ddot {u}}}_{b}+{\hat {r}}_{u}-{\hat {f}}_{u}\right)=&0\quad \forall \;\delta {\hat {u}}_{u}\in \mathbb {R} ^{m_{u}}\,,\end{aligned}}$

wenn m_u die Dimension des Vektors $\hat{u}_u$ ist. Die obige Gleichung erzwingt das Verschwinden der Summe in den runden Klammern mit dem Resultat:

$M_{uu}{\hat {\ddot {u}}}_{u}={\hat {f}}_{u}-{\hat {r}}_{u}-M_{ub}{\hat {\ddot {u}}}_{b}\,.$

Sobald die Verschiebungen vollständig ermittelt wurden, ist es üblich – falls gewünscht – aus der herausgefallenen unteren Gleichungszeile die Reaktionen an den Lagerungen zu berechnen, beispielsweise:

${\hat {r}}_{b}=-M_{bu}{\hat {\ddot {u}}}_{u}-M_{bb}{\hat {\ddot {u}}}_{b}\,.$

Im Text angenommene Vereinfachungen

Der Einfachheit halber werden im Folgenden nur statische Festlager betrachtet in denen die Verschiebungen und Beschleunigungen null sind. Dann treten diese Verschiebungen und Beschleunigungen im Gleichungssystem nicht auf und auf eine Partitionierung in unbekannte und bekannte Anteile kann verzichtet werden. Der Vektor ${\hat {u}}$ mit den Unbekannten habe nach wie vor die Dimension m. Dann folgt aus der Gleichung $\delta {\hat {u}}^{\top }[M{\hat {\ddot {u}}}+{\hat {r}}-{\hat {f}}]=0\quad \forall \;\delta {\hat {u}}\in \mathbb {R} ^{m}$ (PvdA) unmittelbar die Bewegungsgleichung:

$M{\hat {\ddot {u}}}={\hat {f}}-{\hat {r}}\,.$		(*)

Des Weiteren soll im Folgenden jede Abhängigkeit von den Geschwindigkeiten, wie sie bei viskosen Materialien oder geschwindigkeitsabhängigen Kräften vorliegt, der Einfachheit halber vernachlässigbar sein.

Verschiebungen und Beschleunigungen

In der Matrizengleichung $M{\hat {\ddot {u}}}={\hat {f}}-{\hat {r}}$ (*) kommen die Knotenbeschleunigungen ${\hat {\ddot {u}}}$ vor, aber in der Verschiebungsmethode sind die Verschiebungen die primären Unbekannten. Hier soll geklärt werden, wie aus den Verschiebungen standardmäßig die Beschleunigungen ermittelt werden.

Die Beschleunigungen sind die zweite Ableitung der Verschiebungen nach der Zeit und daher sind die Beschleunigungen und Verschiebungen nicht voneinander unabhängig, vielmehr kann die eine aus der anderen über Zeitintegration oder -ableitung berechnet werden. Üblicherweise werden für die Zeitintegration Einschrittverfahren eingesetzt, in denen die Verschiebungen und Beschleunigungen zur Zeit $t^{n+1}$ aus zur Zeit t^n bekannten Werten berechnet werden. Weit verbreitet sind vor allem zwei Zeitintegrationsverfahren:

Das implizite Newmark-beta-Verfahren und
die explizite Zeitintegration.

Im Newmark-beta-Verfahren sollen hier die Verschiebungen als primäre Unbekannte benutzt werden, die gemäß

$\hat{\ddot{u}}^{n+1} = p\hat{u}^{n+1}+\hat{p}^n$		(NbV)

Beschleunigungen bewirken. Der Parameter kommt aus dem Integrationsalgorithmus und der Vektor $\hat{p}^n$ ist zur Zeit t^n bekannt.^[1] In der expliziten Zeitintegration ist

$\hat{u}^{n+1}=q\hat{\ddot{u}}^n+\hat{q}^n\,.$		(EZI)

Der Skalar ist auch ein Parameter des Integrationsalgorithmus und der Vektor $\hat{q}^n$ ist zur Zeit t^n bekannt.^[2]

Diese Ergebnisse werden bei der Lösung der Matrizengleichungen benötigt.

Anwendungen

Linearer Fall

Im linearen Fall hängen die Spannungen ${\hat {T}}$ linear von den Knotenverschiebungen (aber nach Voraussetzung nicht von den Geschwindigkeiten) ab:

${\hat {T}}={\hat {T}}^{0}+C_{L}{\hat {E}}_{L}={\hat {T}}^{0}+C_{L}B_{L}{\hat {u}}\,.$

Der Vektor ${\hat {T}}^{0}$ enthält Eigenspannungen und die Stoffmatrix $C_{L}$ ist bei Linearität von den Verzerrungen und damit von den Knotenverschiebungen unabhängig. Die Verzerrungen sind ebenfalls linear in den Verschiebungen $({\hat {E}}_{L}=B_{L}{\hat {u}})\,,$ was auch für die virtuellen Verzerrungen gilt. Damit berechnen sich die Reaktionen zu

${\hat {r}}=\int _{V}B_{L}^{\top }{\hat {T}}\,{\text{d}}V=\underbrace {\int _{V}B_{L}^{\top }{\hat {T}}^{0}\,{\text{d}}V} _{{\hat {r}}_{L}^{0}}+\underbrace {\int _{V}B_{L}^{\top }C_{L}B_{L}\,{\text{d}}V} _{K_{L}}{\hat {u}}={\hat {r}}_{L}^{0}+K_{L}{\hat {u}}$

Die lineare Steifigkeitsmatrix K_L ist von den Verschiebungen unabhängig. Einsetzen in die Bewegungsgleichung $M{\hat {\ddot {u}}}={\hat {f}}-{\hat {r}}$ (*) liefert zu einer Zeit tⁿ⁺¹ die Bestimmungsgleichung für die Knotenverschiebungen:

$\rightarrow M\hat{\ddot{u}}^{n+1}+K_{L}\hat{u}^{n+1} =\hat{f}^{n+1}-\hat{r}^{0}_{L} \,.$

Freie Schwingung eines einseitig eingespannten Balkens

Diese lineare Gleichung mit von den Verzerrungen unabhängiger Massenmatrix und Steifigkeitsmatrix $K_{L}$ kann in den Modalraum übertragen werden, mit einem Resultat wie im Bild.

In dem im Newmark-beta-Verfahren die Beschleunigungen mit den Verschiebungen gemäß $\hat{\ddot{u}}^{n+1} = p\hat{u}^{n+1}+\hat{p}^n$ ^[1] ausgedrückt werden, kann in jedem Zeitschritt die Verschiebung berechnet werden:

$(pM+K_{L}){\hat {u}}^{n+1}={\hat {f}}^{n+1}-{\hat {r}}_{L}^{0}-M{\hat {p}}^{n}\,.$

Ist nur die Gleichgewichtslage mit $\hat{\ddot{u}} =\hat{0}$ gesucht, ergeben sich die Verschiebungen aus

$K_{L}\hat{u}^{n+1} =\hat{f}^{n+1}-\hat{r}^{0}_{L} \,.$

Auch wenn im linearen Fall eine lineare Abhängigkeit der äußeren Kräfte $\hat{f}$ von den Knotenverschiebungen einfach zu berücksichtigen wäre, wird hiervon normalerweise kein Gebrauch gemacht.

Implizite Lösung nichtlinearer Probleme

Geometrisch nichtlineare Analyse eines beulenden, elastoplastischen Trägers

Die Knotenreaktion $\hat r$ in der Bewegungsgleichung $M{\hat {\ddot {u}}}={\hat {f}}-{\hat {r}}$ (*) hängt im nichtlinearen Fall nichtlinear von den Knotenverschiebungen ${\hat {u}}$ ab. Ursachen der Nichtlinearität können sein:

Materielle Nichtlinearität: Plastizität, nichtlineare Elastizität.

Verschiebungsabhängige Randbedingungen: Von der Verformung abhängende Kräfte, Körperkontakt.

Geometrische Nichtlinearität: Große Drehungen oder Verformungen, Knicken, Beulen.

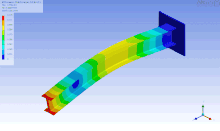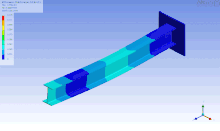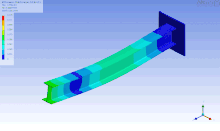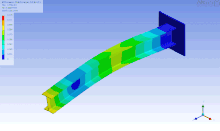
Die Animation zeigt eine geometrisch nichtlineare, implizite Analyse eines beulenden, elastoplastischen Trägers.

Um die Knotenverschiebungen zu bestimmen, wird standardmäßig das Newton-Verfahren eingesetzt, das eine Linearisierung der Gleichung vorsieht. Linearisierung der Reaktionen $\hat{r}$ liefert im Punkt $\hat{u}^i\,:$ ^[3]

${\begin{aligned}{\hat {r}}({\hat {u}}^{i}+\Delta {\hat {u}})=&\int _{V}B^{\top }({\hat {u}}^{i}+\Delta {\hat {u}}){\hat {T}}({\hat {u}}^{i}+\Delta {\hat {u}})\mathrm {d} V\\[-2ex]\approx &\underbrace {\int _{V}B^{i\top }{\hat {T}}^{i}\mathrm {d} V} _{{\hat {r}}^{i}}+\underbrace {\int _{V}{\frac {\mathrm {d} }{\mathrm {d} {\hat {u}}}}\left.(B^{i\top }{\hat {T}}^{i})\right|_{{\hat {T}}^{i}={\text{const.}}}\mathrm {d} V} _{G^{i}}\Delta {\hat {u}}+\underbrace {\int _{V}B^{i\top }\overbrace {\frac {\mathrm {d} {\hat {T}}}{\mathrm {d} {\hat {E}}}} ^{C}\overbrace {\frac {\mathrm {d} {\hat {E}}}{\mathrm {d} {\hat {u}}}} ^{B^{i}}\mathrm {d} V} _{K^{i}}\Delta {\hat {u}}\\=&{\hat {r}}^{i}+(G^{i}+K^{i})\Delta {\hat {u}}\,.\end{aligned}}$

Die mit dem Superskript $(\cdot)^i$ gekennzeichneten Größen können von den Verschiebungen $\hat{u}^i$ abhängen. Die B-Matrix tut das nur im geometrisch nichtlinearen Fall und nur in diesem Fall muss also die geometrische Steifigkeitsmatrix G^i aufgestellt werden.

Bei verschiebungsabhängigen äußeren Kräften wird auch der Knotenkraftvektor $\hat{f}$ linearisiert^[3]

${\hat {f}}({\hat {u}}^{i}+\Delta {\hat {u}})\approx {\hat {f}}({\hat {u}}^{i})+{\frac {\mathrm {d} {\hat {f}}}{\mathrm {d} {\hat {u}}}}\Delta {\hat {u}}=:{\hat {f}}^{i}+F^{i}\Delta {\hat {u}}\,,$

was auf eine m×m Matrix Fⁱ führt. In dynamischen Systemen bewirkt das Verschiebungsinkrement auch ein Beschleunigungsinkrement: $\Delta\hat{\ddot{u}} = p\Delta\hat{u}\,.$ ^[1] Einsetzen dieser Resultate in die Bewegungsgleichung $M{\hat {\ddot {u}}}={\hat {f}}-{\hat {r}}$ (*) liefert mit der Abkürzung $K_{NL}=G^{i}+K^{i}-F^{i}\,:$

$(pM+K_{NL}^i)\Delta\hat{u} =\hat{f}^i-\hat{r}^i-M\hat{\ddot{u}}^i =:\hat{b}^i_{I} \,.$		(I)

Ist nur die Gleichgewichtslage mit $\hat{\ddot{u}} =\hat{0}$ gesucht, reduziert sich das auf

$K_{NL}^{i}\Delta {\hat {u}}={\hat {f}}^{i}-{\hat {r}}^{i}=:{\hat {b}}_{II}^{i}\,.$		(II)

Die Knotenverschiebungen zu einem Zeitpunkt $t^{n+1}$ werden aus den zur Zeit t^n bekannten Knotenverschiebungen und -beschleunigungen anhand des folgenden Schemas berechnet. Das Schema kann auch im statischen Fall angewendet werden. Dort verschwinden zwar die Beschleunigungen und die Zeit hat lediglich eine ordnende Funktion für die aufeinander folgenden Gleichgewichtslagen. Auf das Schema hat das aber keinen Einfluss.

Die gesuchte Lösung $\hat{u}^{n+1}$ wird mit den bekannten Verschiebungen im letzten Inkrement ${\hat {u}}^{n+1,0}={\hat {u}}^{n}$ (oder dem Nullvektor) und der Iterationszähler mit i=0 initialisiert. In dynamischen Systemen wird die Massenmatrix bereitgestellt. Im Allgemeinen (hier nicht) werden die Randbedingungen in den Lösungsvektor eingetragen und in einen bekannten und einen unbekannten Teil partitioniert.
Die Matrix $K_{NL}^i$ und das Residuum $\hat{b}^i_{I/II}$ werden mit der vorliegenden Näherungslösung ${\hat {u}}^{n+1,i}$ aufgestellt.
Mit Gleichungen (I) oder (II) wird das Inkrement $\Delta\hat{u}$ berechnet.
Fallen geeignete Normen der Vektoren $\Delta\hat{u}$ und $\hat{b}^i_{I/II}$ unter eine vorgegebene Schranke, wird die Näherungslösung ${\hat {u}}^{n+1,i}$ akzeptiert und in den Lösungsvektor $\hat{u}^{n+1}$ übertragen und – falls gewünscht – die Beschleunigungen ${\hat {\ddot {u}}}^{n+1}$ berechnet^[1]. Den Elementen wird Gelegenheit gegeben ihre inneren Variablen zu aktualisieren (siehe #Tangentenoperator C). Der Zähler wird inkrementiert und in Schritt 1 fortgefahren oder die Analyse beendet.
Falls die Normen der Vektoren $\Delta\hat{u}$ oder $\hat{b}^i_{I/II}$ jedoch inakzeptabel sind, wird die Näherungslösung mittels ${\hat {u}}^{n+1,i+1}={\hat {u}}^{n+1,i}+\Delta {\hat {u}}$ aktualisiert, der Zähler inkrementiert und im Schritt 2 fortgefahren.

Explizite Lösung nichtlinearer Probleme

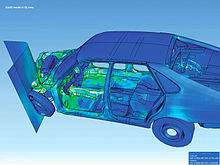
Visualisierung einer FEM-Simulation der Verformung eines Autos bei asymmetrischem Frontalaufprall

Im Fall der expliziten Zeitintegration ist die Bewegungsgleichung $M{\hat {\ddot {u}}}={\hat {f}}-{\hat {r}}$ (*) bereits die Bestimmungsgleichung für die einzige Unbekannte $\hat{\ddot{u}}^{n+1}\,,$ denn die Vektoren $\hat r$ und ${\hat f}$ werden aus zur Zeit t^n bekannten Größen berechnet:

$M\hat{\ddot{u}}^{n+1}=\hat{f}^n-\hat{r}^n\,.$

Aus den Beschleunigungen werden die Geschwindigkeiten und Verschiebungen für die Berechnung der Reaktionskräfte $\hat{r}$ für das nächste Inkrement ermittelt, siehe explizite Zeitintegration im Vergleich zum Newmark-beta-Verfahren. Eine weitere Vereinfachung wird durch Diagonalisierung der Massenmatrix erreicht ( engl. "lumped mass matrix" ), so dass

${\hat {\ddot {u}}}^{n+1}=M^{-1}({\hat {f}}^{n}-{\hat {r}}^{n})$

besonders schnell ausgewertet werden kann. Das ist auch nötig, denn dieses Verfahren ist nur unterhalb einer kritischen Zeitschrittweite $\Delta t_{c}$ stabil, die sich gemäß der Courant-Friedrichs-Lewy-Bedingung danach bemisst, wie lange ein Signal braucht, um von einem Knoten zum nächsten zu gelangen. Ist der minimale Knotenabstand $l_{c}=10\,\mathrm {mm} \,,$ berechnet sich bei Stahlbauteilen mit einem Elastizitätsmodul $E=200.000\,{\mathrm {MPa}}$ (Megapascal) und einer Dichte $\rho =7870\,{\frac {{\mathrm {kg}}}{{\mathrm {m}}^{3}}}$ :

$\Delta t_c\le\frac{l_c}{c} =\frac{l_c}{\sqrt{\frac{E}{\rho}}} \approx 2\cdot 10^{-6}\mathrm{s}$

worin die Wellenausbreitungsgeschwindigkeit in Stahl ist. Bei diesen in der Praxis üblichen Werten liegt die kritische Zeitschrittweite also im Bereich von Mikrosekunden. Für Zehntelsekunden andauernde Bewegungen sind daher oftmals zehntausende Zeitschritte zu berechnen. Vorteilhaft ist, dass Nichtlinearitäten ohne Linearisierung berücksichtigt werden können, weshalb dieses Verfahren bei nichtlinearen, dynamischen und kurzzeitigen Vorgängen wie Crashtestsimulationen eingesetzt wird, siehe Bild. Ein weiterer Vorteil ist, dass der Aufwand für die Berechnung der Beschleunigungen nur linear mit der Dimension des Lösungsvektors ${\hat {u}}$ steigt, so dass sich dieses Verfahren auch für sehr große Probleme unter quasi statischen Bedingungen anbietet.

Elementmatrizen an den Integrationspunkten

Die Integrale, die im Prinzip von d’Alembert in der Lagrangeschen Fassung vorkommen, können im allgemeinen Anwendungsfall nicht exakt integriert werden. Stattdessen werden die Volumenintegrale mit numerischen Integrationsverfahren wie der Gauß-Quadratur berechnet, bei der das Integral als Summe gewichteter Integranden an Integrationspunkten angenähert wird.

In diesem Abschnitt werden die oben auftretenden Matrizen, die an jedem Integrationspunkt aufzubauen sind, angegeben.

Formfunktionen N und ihre Ableitungen

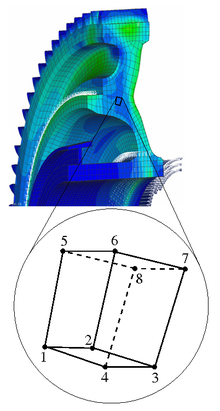
Ein acht knotiges Hexaeder-Element als Teilkörper eines Zahnrades

Jedes Element modelliert ein von den Knoten aufgespanntes dreidimensionales Volumen des Körpers. Das Bild zeigt als Illustration ein acht knotiges Hexaeder-Element als Teilkörper eines Zahnrades. Die Koordinaten $\vec{X}$ der Punkte im Element werden mit Formfunktionen N^i in Abhängigkeit von lokalen Koordinaten

$\vec{\Theta}=\begin{pmatrix}\xi\\\eta\\\zeta\end{pmatrix}\in [-1,1]^{3}$

zwischen den k Knoten des Elementes interpoliert:

$\vec{X} =\begin{pmatrix} X\\Y\\Z\end{pmatrix} =\sum_{i=1}^{k} N^i(\vec{\Theta})\vec{X}^i =N(\vec{\Theta})\hat{X}\,,$

Der 3k × 1 Vektor $\hat{X}$ enthält alle Komponenten der Knotenkoordinaten $\vec{X}^{1\ldots k}$

$\hat{X} =\begin{pmatrix} X^{1} & Y^{1} & Z^{1} & X^{2} & Y^{2} & Z^{2} &\ldots & X^{k} & Y^{k} & Z^{k} \end{pmatrix}^\top$

und die 3 × 3k Matrix

$N =\begin{pmatrix} N^{1}& 0& 0& N^{2}& 0& 0&\ldots& N^{k}& 0& 0\\ 0& N^{1}& 0& 0& N^{2}& 0&\ldots& 0& N^{k}& 0\\ 0& 0& N^{1}& 0& 0& N^{2}&\ldots& 0& 0& N^{k} \end{pmatrix}$

die Formfunktionen $N^{1\ldots k}\,.$ Das Argument ${\vec {\Theta }}$ der Formfunktionen wurde hier der Übersichtlichkeit halber weggelassen und das soll auch im Folgenden geschehen.

Die Ableitung der Formfunktionen nach den globalen Koordinaten $X,\,Y,\,Z$ wird mit der Jacobi-Matrix berechnet:

$\begin{pmatrix} N_{,\xi}^i\\ N_{,\eta}^i\\ N_{,\zeta}^i \end{pmatrix} = \underbrace{\begin{pmatrix} X_{,\xi}& Y_{,\xi}& Z_{,\xi}\\ X_{,\eta}& Y_{,\eta}& Z_{,\eta}\\ X_{,\zeta}& Y_{,\zeta}& Z_{,\zeta} \end{pmatrix}}_{J^\top} \begin{pmatrix} N_{,X}^i\\ N_{,Y}^i\\ N_{,Z}^i \end{pmatrix} \quad\Leftrightarrow\quad \begin{pmatrix} N_{,X}^i\\ N_{,Y}^i\\ N_{,Z}^i \end{pmatrix} = \underbrace{\begin{pmatrix} \xi_{,X}&\eta_{,X}&\zeta_{,X}\\ \xi_{,Y}&\eta_{,Y}&\zeta_{,Y}\\ \xi_{,Z}&\eta_{,Z}&\zeta_{,Z} \end{pmatrix}}_{J^{\top-1}} \begin{pmatrix} N_{,\xi}^i\\ N_{,\eta}^i\\ N_{,\zeta}^i \end{pmatrix} \,.$

Ein Index $(\cdot)_{,x}$ nach einem Komma bedeutet hier wie im Folgenden eine Ableitung nach der Variablen $x\,.$ Die Matrix $J^{\top-1}$ ist die transponiert inverse Jacobimatrix. Weil die Invertierung der Jacobimatrix bei der Koordinatentransformation immer gelingt und die Ableitung nach den lokalen Koordinaten $\xi,\,\eta,\,\zeta$ analytisch machbar ist, ergeben sich aus der rechten Gleichung die gesuchten Ableitungen nach den globalen Koordinaten. Mit der Determinante der Jacobimatrix werden die für die Integration benötigten vektoriellen Oberflächenelemente und Volumenformen umgerechnet:

${\begin{aligned}\mathrm {d} {\vec {A}}=&{\vec {\varphi }}_{,X}\times {\vec {\varphi }}_{,Y}\,\mathrm {d} X\,\mathrm {d} Y=\mathrm {det} (J)J^{\top -1}{\vec {\varphi }}_{,\xi }\times {\vec {\varphi }}_{,\eta }\,\mathrm {d} \xi \,\mathrm {d} \eta \\\mathrm {d} V=&\mathrm {d} X\,\mathrm {d} Y\,\mathrm {d} Z=\mathrm {det} (J)\,\mathrm {d} \xi \,\mathrm {d} \eta \,\mathrm {d} \zeta \,.\end{aligned}}$

Hier wurde beispielhaft eine durch die Koordinaten X und Y beschreibbare Fläche $\vec{\varphi}(X,Y)$ angenommen.

Verschiebungen und ihr Gradient H

Der Verschiebungsvektor wird in isoparametrischen Elementen analog zum Ortsvektor interpoliert:

$\vec{u} =\begin{pmatrix}u\\ v\\ w\end{pmatrix} =\sum_{i=1}^{k} N^i\vec{u}^i =N\hat{u}$

Der 3k × 1 Vektor ${\hat {u}}$ enthält die Verschiebungskomponenten $u,\,v$ und in x-, y- bzw. z-Richtung an den Knoten

$\hat{u} =\begin{pmatrix} u^{1}& v^{1}& w^{1}& u^{2}& v^{2}& w^{2}&\ldots& u^{k}& v^{k}& w^{k} \end{pmatrix}^\top$

Es wird noch der Verschiebungsgradient erstellt^[3]

$\mathbf{H} =\mathrm{GRAD}(\vec{u}) =\frac{\mathrm{d}\vec{u}}{\mathrm{d}\vec{X}} =\begin{pmatrix}\vec{u}_{,X}&\vec{u}_{,Y}&\vec{u}_{,Z}\end{pmatrix} =\begin{pmatrix} u_{,X}& u_{,Y}& u_{,Z}\\ v_{,X}& v_{,Y}& v_{,Z}\\ w_{,X}& w_{,Y}& w_{,Z} \end{pmatrix}\,.$

Die Ableitungen der Verschiebungskomponenten werden mit den abgeleiteten Formfunktionen berechnet, z.B.

$\vec{u}_{,X} =\begin{pmatrix} u_{,X}\\ v_{,X}\\ w_{,X}\end{pmatrix} =\sum_{i=1}^{k} N_{,X}^i\vec{u}^i =N_{,X}\hat{u}\,.$

In der Galerkin-Methode werden die virtuellen Verschiebungen, die im Prinzip von d’Alembert vorkommen, genauso behandelt wie die Knotenverschiebungen:

$\delta\vec{u} =\begin{pmatrix} \delta u\\\delta v\\\delta w \end{pmatrix} =\sum_{i=1}^{k} N^i\delta\vec{u}^i =N\delta\hat{u}\,.$

Verzerrungsverschiebungsmatrix B

Der symmetrische Green-Lagrange-Verzerrungstensor ergibt sich aus dem Verschiebungsgradient gemäß

$\mathbf{E} =\frac{1}{2}( \mathbf{H}+\mathbf{H}^\top+\mathbf{H}^\top\cdot\mathbf{H}) \,.$

Seine sechs unabhängigen Komponenten werden in einen Vektor eingetragen (Voigtsche Notation):

${\hat {E}}:={\begin{pmatrix}E_{xx}&E_{yy}&E_{zz}&2E_{xy}&2E_{yz}&2E_{xz}\end{pmatrix}}^{\top }\,.$

Die Verzerrungsverschiebungsmatrix ist die Ableitung^[3] des Vektors ${\hat {E}}$ nach den Knotenverschiebungen:

$B={\frac {\mathrm {d} {\hat {E}}}{\mathrm {d} {\hat {u}}}}\in \mathbb {R} ^{6\times 3k}\quad \leftrightarrow \quad B_{ij}={\frac {{\textrm {d}}E_{i}}{{\textrm {d}}{\hat {u}}_{j}}}\quad {\text{für}}\quad i=1,2,...,6\quad {\text{und}}\quad j=1,2,...,3k\,.$

Die differenziellen virtuellen Verzerrungen $\delta {\hat {E}}$ ergeben sich dann mit der B-Matrix aus den virtuellen Knotenverschiebungen $\delta\hat{u}$ :

$\delta {\hat {E}}=B\delta {\hat {u}}\,.$

Geometrisch linearer Fall

Im geometrisch linearen Fall sind die Verzerrungen

$\mathbf {E} _{L}:={\frac {1}{2}}(\mathbf {H} +\mathbf {H} ^{\top })\quad \rightarrow \quad {\hat {E}}_{L}={\begin{pmatrix}u_{,X}\\v_{,Y}\\w_{,Z}\\u_{,Y}+v_{,X}\\v_{,Z}+w_{,Y}\\u_{,Z}+w_{,X}\end{pmatrix}}$

linear in den Knotenverschiebungen, weshalb sich die B-Matrix durch "Ausklammern" der Knotenverschiebungen ergibt und die übersichtliche Form

$B = B_L :=\begin{pmatrix} N_{,X}^{1}& 0& 0& N_{,X}^{2}& 0& 0&\ldots& N_{,X}^{k}& 0& 0\\ 0& N_{,Y}^{1}& 0& 0& N_{,Y}^{2}& 0&\ldots& 0& N_{,Y}^{k}& 0\\ 0& 0& N_{,Z}^{1}& 0& 0& N_{,Z}^{2}&\ldots& 0& 0& N_{,Z}^{k}\\ N_{,Y}^{1}& N_{,X}^{1}& 0 & N_{,Y}^{2}& N_{,X}^{2}& 0&\ldots& N_{,Y}^{k}& N_{,X}^{k}& 0\\ 0& N_{,Z}^{1}& N_{,Y}^{1}& 0& N_{,Z}^{2}& N_{,Y}^{2}&\ldots& 0& N_{,Z}^{k}& N_{,Y}^{k}\\ N_{,Z}^{1}& 0& N_{,X}^{1}& N_{,Z}^{2}& 0& N_{,X}^{2}&\ldots& N_{,Z}^{k}& 0& N_{,X}^{k} \end{pmatrix}$

besitzt. Dann gilt: ${\hat {E}}_{L}=B_{L}{\hat {u}}\,.$

Geometrisch nichtlinearer Fall

Im geometrisch nichtlinearen Fall muss zur geometrisch linearen B-Matrix $B_{L}$ noch ein Anteil aus

$\mathbf{E}_{NL}=\frac{1}{2}\mathbf{H}^\top\cdot\mathbf{H}$

addiert werden, der auf die Matrix

$B_{NL}=\begin{pmatrix} B_{NL}^{1}& B_{NL}^{2}&\dots & B_{NL}^{k} \end{pmatrix}$

mit den Blöcken

$B_{NL}^{i}={\frac {\mathrm {d} {\hat {E}}_{NL}}{\mathrm {d} {\vec {u}}^{i}}}={\begin{pmatrix}u_{,X}N_{,X}^{i}&v_{,X}N_{,X}^{i}&w_{,X}N_{,X}^{i}\\u_{,Y}N_{,Y}^{i}&v_{,Y}N_{,Y}^{i}&w_{,Y}N_{,Y}^{i}\\u_{,Z}N_{,Z}^{i}&v_{,Z}N_{,Z}^{i}&w_{,Z}N_{,Z}^{i}\\u_{,X}N_{,Y}^{i}+u_{,Y}N_{,X}^{i}&v_{,X}N_{,Y}^{i}+v_{,Y}N_{,X}^{i}&w_{,X}N_{,Y}^{i}+w_{,Y}N_{,X}^{i}\\u_{,Y}N_{,Z}^{i}+u_{,Z}N_{,Y}^{i}&v_{,Y}N_{,Z}^{i}+v_{,Z}N_{,Y}^{i}&w_{,Y}N_{,Z}^{i}+w_{,Z}N_{,Y}^{i}\\u_{,X}N_{,Z}^{i}+u_{,Z}N_{,X}^{i}&v_{,X}N_{,Z}^{i}+v_{,Z}N_{,X}^{i}&w_{,X}N_{,Z}^{i}+w_{,Z}N_{,X}^{i}\end{pmatrix}}$

führt. Die resultierende B-Matrix

$B = B_L +B_{NL}$

ist in diesem Fall von den Knotenverschiebungen ${\hat {u}}$ abhängig.

Tangentenoperator C

Die Spannungen werden wie die Dehnungen in einen Vektor eingetragen

${\hat {T}}={\begin{pmatrix}{\tilde {T}}_{xx}&{\tilde {T}}_{yy}&{\tilde {T}}_{zz}&{\tilde {T}}_{xy}&{\tilde {T}}_{yz}&{\tilde {T}}_{xz}\end{pmatrix}}^{\top }\,.$

Auf Elementebene muss eine Materialroutine ${\mathcal {T}}$ diese Spannungen aus Spannungen ${\hat {T}}^{n}$ im letzten Zeitschritt $t^n\,,$ einem Verzerrungsinkrement $\Delta {\hat {E}}$ und eventuell weiteren inneren Variablen V^n des Materialmodells berechnen:

${\hat {T}}^{i}={\mathcal {T}}({\hat {T}}^{n},\Delta {\hat {E}},V^{n})\,.$

Bei linearer Elastizität sind die Spannungen linear in den Verzerrungen ${\hat {T}}^{i}={\hat {T}}^{n}+C_{L}\Delta {\hat {E}}\,.$ Die 6×6 Matrix $C_{L}$ ist dann die von den Verzerrungen unabhängige Elastizitätsmatrix. Für die Anwendung des Newton-Verfahrens bei der Berechnung von Problemen mit nichtlinearem Materialverhalten muss die Ableitung der Spannungen nach den Verzerrungen bereitgestellt werden, was auf den konsistenten Tangentenoperator führt, der ebenfalls eine 6×6 Matrix ist. Bei linearer Elastizität ist $C = C_L\,.$ Der Tangentenoperator ergibt sich aus der Ableitung der Spannungen nach den Verzerrungen an der Stelle der aktuellen Spannungen ${\hat {T}}^{i}$ (und inneren Variablen, deren aktueller Wert bei der Berechnung der Spannungen anfällt):

$C_{NL}H=\lim _{s\rightarrow 0}{\frac {{\mathcal {T}}({\hat {T}}^{i},sH,V^{i})-{\hat {T}}^{i}}{s}}\quad \forall \;H\in \mathbb {R} ^{6}\quad \rightarrow \;C=C_{NL}\,.$

Dann kann

$C={\frac {\mathrm {d} {\hat {T}}^{i}}{\mathrm {d} {\hat {E}}}}$

geschrieben werden. Die Konsistenz bezieht sich darauf, dass der Tangentenoperator aus der Ableitung der Materialroutine ${\mathcal {T}}$ und nicht im analytischen Materialmodell berechnet wird, das durch ${\mathcal {T}}$ numerisch umgesetzt wird.

Geometrische Steifigkeitsmatrix G

Die Geometrische Steifigkeitsmatrix

$G^{i}:=\int _{V}{\frac {\mathrm {d} }{\mathrm {d} {\hat {u}}}}\left.(B^{i\top }{\hat {T}}^{i})\right|_{{\hat {T}}^{i}={\text{const.}}}\mathrm {d} V=\int _{V}{\begin{pmatrix}D(g_{11})&\ldots &D(g_{1k})\\\vdots &\ddots &\vdots \\D(g_{k1})&\ldots &D(g_{kk})\end{pmatrix}}\,\mathrm {d} V$

hat eine Blockstruktur mit Blöcken aus Diagonalmatrizen

$D(g_{mn}) :=\frac{1}{2}\begin{pmatrix} g_{mn}& 0& 0\\ 0& g_{mn}& 0\\ 0& 0& g_{mn} \end{pmatrix}$

und den Diagonalgliedern

${\begin{aligned}g_{mn}=g_{nm}=&{\tilde {T}}_{1}^{i}N_{,X}^{m}N_{,X}^{n}+{\tilde {T}}_{2}^{i}N_{,Y}^{m}N_{,Y}^{n}+{\tilde {T}}_{3}^{i}N_{,Z}^{m}N_{,Z}^{n}+{\tilde {T}}_{4}^{i}(N_{,X}^{m}N_{,Y}^{n}+N_{,Y}^{m}N_{,X}^{n})\\&+{\tilde {T}}_{5}^{i}(N_{,Y}^{m}N_{,Z}^{n}+N_{,Z}^{m}N_{,Y}^{n})+{\tilde {T}}_{6}^{i}(N_{,X}^{m}N_{,Z}^{n}+N_{,Z}^{m}N_{,X}^{n})\end{aligned}}$

Beispiel

Stab mit variablem Querschnitt unter Einzelkraftbelastung.

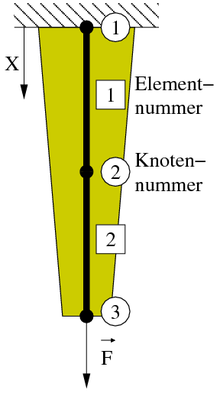
Die Längung eines einseitig eingespannten Zugstabes mit linear abnehmender Querschnittsfläche unter Einzelkraft am Ende, wie im Bild, soll berechnet werden. Dazu wird ein in x-Richtung liegendes, eindimensionales, zweiknotiges Stabelement konstruiert. Die x-Koordinate der Punkte im Stab, die Formfunktionsmatrix und Knotenkoordinaten bilden den Zusammenhang

${\begin{aligned}X=&N{\hat {X}}={\frac {1}{2}}{\begin{pmatrix}1-\xi &1+\xi \end{pmatrix}}{\begin{pmatrix}X^{1}\\X^{2}\end{pmatrix}}\\=&{\frac {1}{2}}(X^{1}+X^{2})+{\frac {1}{2}}(X^{2}-X^{1})\xi =:{\frac {1}{2}}(R+L\xi )\,,\end{aligned}}$

mit $\xi \in [-1,1]\,.$ Die Jacobi-Matrix degeneriert zu einer Zahl:

$J=X_{,\xi }={\frac {L}{2}}\,.$

Mit ihrer Inversen berechnet sich die Ableitung der Formfunktionsmatrix:

$N_{,X}=J^{-1}N_{,\xi }={\frac {2}{L}}{\frac {1}{2}}{\begin{pmatrix}-1&1\end{pmatrix}}={\frac {1}{L}}{\begin{pmatrix}-1&1\end{pmatrix}}\,.$

Die Verschiebungen, die Formfunktionsmatrix und Knotenverschiebungen bilden den Zusammenhang

$u=N{\hat {U}}={\frac {1}{2}}{\begin{pmatrix}1-\xi &1+\xi \end{pmatrix}}{\begin{pmatrix}U^{1}\\U^{2}\end{pmatrix}}\,.$

Im geometrisch linearen Bereich lauten die Dehnungen und die Verzerrungsverschiebungsmatrix

$E_{L}=u_{,X}=N_{,X}{\hat {U}}={\frac {1}{L}}{\begin{pmatrix}-1&1\end{pmatrix}}{\begin{pmatrix}U^{1}\\U^{2}\end{pmatrix}}=B_{L}{\hat {U}}\quad \rightarrow \quad B_{L}={\frac {1}{L}}{\begin{pmatrix}-1&1\end{pmatrix}}\,.$

Von den Dehnungen gibt es hier nur eine konstante Komponente in Stabrichtung und gleiches gilt für die Spannungen:

$T=CE_{L}=CB_{L}{\hat {U}}\,,$

worin von der Elastizitätsmatrix C_L auch nur eine Komponente C benötigt wird. Die Querschnittsfläche wird mit zwei Parametern a und b beschrieben: A=a-bX. Damit wird das Volumenelement $\mathrm {d} V=A\operatorname {det} (J)\,\mathrm {d} \xi ={\tfrac {L}{2}}(a-bX)\,\mathrm {d} \xi \,.$

Jetzt können die Reaktionen berechnet werden:

${\begin{aligned}{\hat {r}}=&\int _{V}B_{L}^{\top }CB_{L}\,\mathrm {d} V{\hat {U}}=\int _{-1}^{1}{\frac {C}{L^{2}}}{\begin{pmatrix}1&-1\\-1&1\end{pmatrix}}{\frac {L}{2}}(a-bX)\,\mathrm {d} \xi {\hat {U}}\\=&\int _{-1}^{1}\left[a-{\frac {b}{2}}(R+L\xi )\right]\,\mathrm {d} \xi {\frac {C}{2L}}{\begin{pmatrix}1&-1\\-1&1\end{pmatrix}}{\hat {U}}\,.\end{aligned}}$

Das Integral berechnet sich zu

$\int _{-1}^{1}\left[a-{\frac {b}{2}}(R+L\xi )\right]\,\mathrm {d} \xi =\left[a\xi -{\frac {b}{2}}\left(R\xi +L{\frac {\xi ^{2}}{2}}\right)\right]_{-1}^{1}=2\left(a-b{\frac {R}{2}}\right)=2A_{m}\,,$

wenn A_m die Querschnittsfläche des Stabes in der Mitte des Elementes ist. Damit steht die Steifigkeitsmatrix fest:

${\hat {r}}=K_{L}{\hat {U}}\quad \rightarrow \quad K_{L}=C{\frac {A_{m}}{L}}{\begin{pmatrix}1&-1\\-1&1\end{pmatrix}}\,.$

Die äußere Kraft berechnet sich aus einer konstanten Spannung σ am Ende des Stabes bei $\xi =1:$

${\hat {f}}=\int _{A^{\sigma }}N^{\top }{\vec {t}}_{0}\,\mathrm {d} A={\begin{pmatrix}0\\A(\xi =1)\sigma \end{pmatrix}}={\begin{pmatrix}0\\F\end{pmatrix}}\,.$

Zwei Stabelemente halber Länge können zu einem Finite-Elemente-Modell des Stabes zusammengebaut werden. Das zweite Element ergibt sich analog zu den obigen Ausführungen mit den Knotenkoordinaten X² und X³ und den Knotenverschiebungen U² und U³, siehe Bild. Die Freiheitsgrade am Knoten 2 teilen sich beide Elemente. Assemblierung beider Elementbeiträge ergibt:

${\hat {r}}=C{\begin{pmatrix}{\frac {A_{m}^{1}}{L^{1}}}&-{\frac {A_{m}^{1}}{L^{1}}}&0\\-{\frac {A_{m}^{1}}{L^{1}}}&{\frac {A_{m}^{1}}{L^{1}}}+{\frac {A_{m}^{2}}{L^{2}}}&-{\frac {A_{m}^{2}}{L^{2}}}\\0&-{\frac {A_{m}^{2}}{L^{2}}}&{\frac {A_{m}^{2}}{L^{2}}}\end{pmatrix}}{\begin{pmatrix}U^{1}\\U^{2}\\U^{3}\end{pmatrix}}\,.$

Die hochgestellten Indizes geben die Elementnummer an, also keine Potenzierung. Die Elementparameter $A_{m}^{1,2},\,L^{1,2}$ ergeben sich aus den Knotenkoordinaten und den Definitionen für A_m und L. Indem U¹ gleich Null gesetzt wird und eine Kraft F am dritten Knoten angreift berechnen sich die Verschiebungen des zweiten und dritten Knotens aus der Matrizengleichung

$C{\begin{pmatrix}{\frac {A_{m}^{1}}{L^{1}}}+{\frac {A_{m}^{2}}{L^{2}}}&-{\frac {A_{m}^{2}}{L^{2}}}\\-{\frac {A_{m}^{2}}{L^{2}}}&{\frac {A_{m}^{2}}{L^{2}}}\end{pmatrix}}{\begin{pmatrix}U^{2}\\U^{3}\end{pmatrix}}={\begin{pmatrix}0\\F\end{pmatrix}}\,.$

Mit den Parametern in der Tabelle unten berechnet sich U²=0,032 und U³=0,109. In analoger Weise können prinzipiell beliebig viele Stabelemente kombiniert werden.

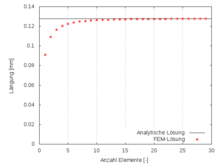
Vergleich der FEM-Lösung (rot) mit der analytischen (schwarz).

Für das Problem gibt es auch eine analytische Lösung. Die Dehnung im Stab ergibt sich – genauso wie im Element – aus ε=u_,X und die Spannungen sind dazu proportional: σ=C ε=C u_,X. Die Längskraft im Stab ist konstant gleich der Zugkraft, verteilt sich aber auf eine abnehmende Querschnittsfläche: F=(a-bX) σ=C(a-bX) u_,X. Diese Differentialgleichung kann mit der Randbedingung u(0)=0 eindeutig gelöst werden:

$u_{,X}={\frac {F}{C(a-bX)}}\quad \rightarrow \quad u(X)={\frac {F}{Cb}}\ln \left({\frac {a}{a-bX}}\right)\,.$

Im Bild rechts ist diese analytische Lösung für die Verschiebung am Ende des Stabes bei X=L mit der FEM-Lösung unter Verwendung der in der Tabelle benutzten Parameter und variabler Elementezahl aufgetragen.

Parameter	L	a	b	C	F
Einheit	mm	mm²	mm	MPa	N
Wert	1000	100	0,09	200.000	1000

Die Konvergenz der FEM-Lösung gegen einen Grenzwert bei zunehmender Netzverfeinerung hat hier einen typischen Verlauf. Er resultiert daraus, dass das Stabelement eine über die Länge konstante Dehnung und Spannung aufweist, die Spannung im Stab aber aufgrund der abnehmenden Querschnittsfläche kontinuierlich zunimmt. Die Annäherung dieses glatten, monoton steigenden Verlaufs durch eine Treppenfunktion im FE-Modell ist immer genauer, je kleiner die Treppenstufen und damit je kleiner die Elemente sind.

Fußnoten

↑ ^a ^b ^c ^d Vergleich der Gleichung

$\hat{\ddot{u}}^{n+1} = p\hat{u}^{n+1}+\hat{p}^n$

(NbV)

mit der Vorschrift für die Aktualisierung der Variablen

$\ddot{x}_{n+1} =\frac{2}{\beta\Delta t^2} (x_{n+1}-x_n) -\frac2{\beta\Delta t}\dot{x}_n -\frac{1-\beta}{\beta}\ddot{x}_n$

ergibt: $p=\tfrac{2}{\beta\Delta t^2}$ und ${\hat {p}}^{n}=-{\tfrac {2}{\beta \Delta t^{2}}}x_{n}-{\frac {2}{\beta \Delta t}}{\dot {x}}_{n}-{\frac {1-\beta }{\beta }}{\ddot {x}}_{n}\,.$
↑ Vergleich der Gleichung

$\hat{u}^{n+1}=q\hat{\ddot{u}}^n+\hat{q}^n\,.$

(EZI)

mit der Vorschrift für die Aktualisierung der Variablen

$x_{n+1} = x_n+\Delta t(\dot{x}_{n-1/2}+\Delta t\ddot{x}_n)$

ergibt: $q=\Delta t^2$ und ${\hat {q}}^{n}=x_{n}+\Delta t{\dot {x}}_{n-1/2}\,.$
↑ ^a ^b ^c ^d Die Ableitung eines n₁×1 Vektors y nach einem n₂×1 Vektor x ist die n₁×n₂ Matrix Z mit den Einträgen

$Z_{ij}=\tfrac{\partial y_i}{\partial x_j}\,,\quad i=1,...,n_1,\, j=1,...,n_2\,.$
Dann wird auch $Z=\frac{\mathrm{d}y}{\mathrm{d}x}$ geschrieben.

Literatur

Klaus-Jürgen Bathe: Finite-Elemente-Methoden: Matrizen und lineare Algebra, die Methode der finiten Elemente, Lösung von Gleichgewichtsbedingungen und Prinzipgleichungen. Springer, 1986, ISBN 3-540-15602-X.
Peter Wriggers: Nichtlineare Finite-Element-Methoden. Springer, 2001, ISBN 3-540-67747-X.

Basierend auf einem Artikel in:

Wikipedia.de