Explizites Euler-Verfahren
Das eulersche Polygonzugverfahren oder explizite Euler-Verfahren (auch Euler-Cauchy-Verfahren oder Euler-vorwärts-Verfahren) ist das einfachste Verfahren zur numerischen Lösung eines Anfangswertproblems.
Es wurde von Leonhard Euler 1768 in seinem Buch Institutiones Calculi Integralis vorgestellt. Cauchy benutzte es, um einige Eindeutigkeitsresultate für gewöhnliche Differentialgleichungen zu beweisen.
Das Verfahren wird manchmal in der Physik als Methode der kleinen Schritte bezeichnet.
Das Verfahren
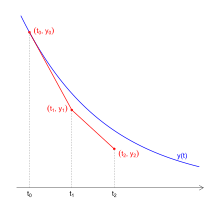
Zur numerischen Lösung des Anfangswert-Problems:
für eine gewöhnliche Differentialgleichung wähle man eine
Diskretisierungs-Schrittweite ,
betrachte die diskreten Zeitpunkte
und berechne die Werte
Die berechneten Werte
stellen Approximationen an die tatsächlichen Werte
der exakten Lösung des Anfangswert-Problems dar. Je kleiner die Schrittweite
gewählt ist, desto mehr Rechenarbeit ist nötig, aber desto genauer werden auch
die approximierten Werte.
Eine Modifikation des Verfahrens besteht hier darin, dass man die Schrittweite variabel wählt. Eine sinnvolle Veränderung der Schrittweite setzt einen Algorithmus zur Schrittweitensteuerung voraus, der den Fehler im aktuellen Schritt abschätzt und dann die Schrittweite für den nächsten Schritt dementsprechend wählt.
Wird ein Verfahren über
definiert, erhält man das implizite
Euler-Verfahren. Dieses ist A-stabil
und daher für steife
Anfangswertprobleme besser geeignet.
Herleitung
Für die Herleitung von Einschrittverfahren wird das Anfangswertproblem meist in die dazu äquivalente Integralgleichung umgeformt
Nun besteht die Idee, beim expliziten Euler-Verfahren eine simple Quadraturformel
für das Integral zu benutzen: die linksseitige
Boxregel. Man wählt in jedem -ten
Schritt den Integranden als konstanten Wert an der linken Intervallgrenze
Eigenschaften
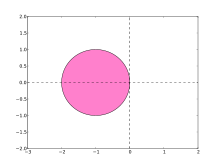
Das explizite Euler-Verfahren hat Konsistenz- und Konvergenzordnung
1. Die Stabilitätsfunktion
ist
und sein Stabilitätsgebiet
daher das Innere des Kreises um −1 mit Radius 1 in der komplexen Zahlenebene.
Verbessertes explizites Euler-Verfahren
Anstatt die Boxregel für die numerische Integration zu verwenden kann man auch die Mittelpunktsregel anwenden.
Nun wendet man wieder das explizite Euler-Verfahren zur Approximation von
an
Zusammen führt dies auf das verbesserte explizite Euler-Verfahren (oder Euler-Verfahren mit kleinerer Schrittweite)
Verallgemeinerungen
Es lässt sich im Wesentlichen durch zwei verschiedene Ideen auf effizientere Verfahren verallgemeinern.
- Die erste Idee ist, bei der Berechnung des nächsten Schrittes mehr als nur einen der zuvor berechneten Werte mit einzubeziehen. Auf diese Weise erhält man Verfahren höherer Ordnung in der Klasse der linearen Mehrschrittverfahren.
- Die zweite Idee ist, bei der Berechnung des nächsten Schrittes die
Funktion
auf dem Intervall
an mehreren Stellen auszuwerten. Auf diese Weise erhält man die Klasse der Runge-Kutta-Verfahren.
Die Klasse der allgemeinen linearen Verfahren bezieht beide Ideen der Verallgemeinerung mit ein und enthält die Klasse der linearen Mehrschrittverfahren sowie die Klasse der Runge-Kutta-Verfahren als Spezialfall.
- Darüber hinaus gibt es auch eine Erweiterung des Euler-Verfahrens für stochastische Differentialgleichungen: das Euler-Maruyama-Verfahren.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 09.07. 2021