Einschrittverfahren

Einschrittverfahren nähern die Lösung (blau) eines Anfangswertproblems an, indem vom gegebenen Startpunkt $A_{0}$ aus nacheinander Punkte $A_{1}$ , $A_{2}$ usw. bestimmt werden

Einschrittverfahren sind in der numerischen Mathematik neben den Mehrschrittverfahren eine große Gruppe von Rechenverfahren zur Lösung von Anfangswertproblemen. Diese Aufgabenstellung, bei der eine gewöhnliche Differentialgleichung zusammen mit einer Startbedingung gegeben ist, spielt in allen Natur- und Ingenieurwissenschaften eine zentrale Rolle und gewinnt beispielsweise auch in den Wirtschafts- und Sozialwissenschaften immer mehr an Bedeutung. Anfangswertprobleme werden verwendet, um dynamische Vorgänge zu analysieren, zu simulieren oder vorherzusagen.

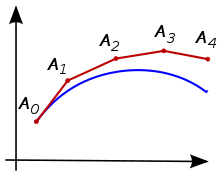
Die namensgebende Grundidee der Einschrittverfahren ist, dass sie ausgehend von dem gegebenen Anfangspunkt Schritt für Schritt entlang der gesuchten Lösung Näherungspunkte berechnen. Dabei verwenden sie jeweils nur die zuletzt bestimmte Näherung für den nächsten Schritt, im Gegensatz zu den Mehrschrittverfahren, die auch weiter zurückliegende Punkte in die Rechnung miteinbeziehen. Die Einschrittverfahren lassen sich grob in zwei Gruppen einteilen: in die expliziten Verfahren, die die neue Näherung direkt aus der alten berechnen, und in die impliziten Verfahren, bei denen dazu eine Gleichung gelöst werden muss. Letztere eignen sich auch für sogenannte steife Anfangswertprobleme.

Das einfachste und älteste Einschrittverfahren, das explizite Euler-Verfahren, wurde 1768 von Leonhard Euler veröffentlicht. Nachdem 1883 eine Gruppe von Mehrschrittverfahren vorgestellt worden war, entwickelten um 1900 Carl Runge, Karl Heun und Wilhelm Kutta deutliche Verbesserungen des eulerschen Verfahrens. Aus diesen ging die große Gruppe der Runge-Kutta-Verfahren hervor, die die wichtigste Klasse von Einschrittverfahren bildet. Weitere Entwicklungen des 20. Jahrhunderts sind beispielsweise die Idee der Extrapolation, vor allem aber Überlegungen zur Schrittweitensteuerung, also zur Wahl geeigneter Längen der einzelnen Schritte eines Verfahrens. Diese Konzepte bilden die Grundlage, um schwierige Anfangswertprobleme, wie sie in modernen Anwendungen auftreten, effizient und mit der benötigten Genauigkeit durch Computerprogramme lösen zu können.

Einführung

Gewöhnliche Differentialgleichungen

Die Entwicklung der Differential- und Integralrechnung durch den englischen Physiker und Mathematiker Isaac Newton und unabhängig davon durch den deutschen Universalgelehrten Gottfried Wilhelm Leibniz im letzten Drittel des 17. Jahrhunderts war ein wesentlicher Impuls für die Mathematisierung der Wissenschaft in der frühen Neuzeit. Diese Methoden bildeten den Startpunkt des mathematischen Teilgebiets der Analysis und sind in allen Natur- und Ingenieurwissenschaften von zentraler Bedeutung. Während Leibniz von dem geometrischen Problem, Tangenten an gegebene Kurven zu bestimmen, zur Differentialrechnung geführt wurde, ging Newton von der Fragestellung aus, wie sich Änderungen einer physikalischen Größe zu einem bestimmten Zeitpunkt bestimmen lassen.

Zum Beispiel ergibt sich bei der Bewegung eines Körpers dessen Durchschnittsgeschwindigkeit einfach als die zurückgelegte Strecke dividiert durch die dafür benötigte Zeit. Um jedoch die Momentangeschwindigkeit v(t) des Körpers zu einem bestimmten Zeitpunkt mathematisch zu formulieren, ist ein Grenzübergang notwendig: Man betrachtet kurze Zeitspannen der Länge $\Delta t$ , die dabei zurückgelegten Wegstrecken $\Delta x$ und die zugehörigen Durchschnittsgeschwindigkeiten ${\tfrac {\Delta x}{\Delta t}}$ . Wenn man nun die Zeitspanne $\Delta t$ gegen null konvergieren lässt und wenn sich dabei die Durchschnittsgeschwindigkeiten ebenfalls einem festen Wert annähern, dann wird dieser Wert die (Momentan-)Geschwindigkeit v(t) zu dem gegebenen Zeitpunkt genannt. Bezeichnet x(t) die Position des Körpers zur Zeit , dann schreibt man $v(t)=x'(t)$ und nennt die Ableitung von .

Der entscheidende Schritt in die Richtung der Differentialgleichungsmodelle ist nun die umgekehrte Fragestellung: Im Beispiel des bewegten Körpers sei also zu jedem Zeitpunkt die Geschwindigkeit v(t) bekannt und daraus soll seine Position x(t) bestimmt werden. Es ist anschaulich klar, dass zusätzlich die Anfangsposition des Körpers zu einem Zeitpunkt $t_{0}$ bekannt sein muss, um dieses Problem eindeutig lösen zu können. Es ist also eine Funktion x(t) mit $x'(t)=v(t)$ gesucht, die die Anfangsbedingung $x(t_{0})=x_{0}$ mit gegebenen Werten $t_{0}$ und $x_{0}$ erfüllt.

Im Beispiel der Bestimmung der Position eines Körpers aus seiner Geschwindigkeit ist die Ableitung der gesuchten Funktion explizit gegeben. Meist liegt jedoch der wichtige allgemeine Fall gewöhnlicher Differentialgleichungen für eine gesuchte Größe vor: Aufgrund der Naturgesetze oder der Modellannahmen ist ein Funktionszusammenhang bekannt, der angibt, wie die Ableitung $y'(t)$ der zu bestimmenden Funktion aus und aus dem (unbekannten) Wert y(t) berechnet werden kann. Zusätzlich muss wieder eine Anfangsbedingung gegeben sein, die beispielsweise aus einer Messung der gesuchten Größe zu einem fest gewählten Zeitpunkt erhalten werden kann. Zusammengefasst liegt also der folgende allgemeine Aufgabentyp vor: Man finde die Funktion , die die Gleichungen

$y'(t)=f(t,y(t)),\quad y(t_{0})=y_{0}$

erfüllt, wobei eine gegebene Funktion ist.

Die dargestellte Lösung der Differentialgleichung des Lorenz-Attraktors ist eine sehr komplizierte Kurve im dreidimensionalen Raum

Ein einfaches Beispiel ist eine Größe , die exponentiell wächst. Das bedeutet, dass die momentane Änderung, also die Ableitung $y'(t)$ proportional zu y(t) selbst ist. Es gilt also $y'(t)=\lambda y(t)$ mit einer Wachstumsrate $\lambda$ und beispielsweise einer Anfangsbedingung $y(0)=y_{0}$ . Die gesuchte Lösung lässt sich in diesem Fall bereits mit elementarer Differentialrechnung finden und mithilfe der Exponentialfunktion angeben: Es gilt $y(t)=y_{0}e^{\lambda t}$ .

Die gesuchte Funktion in einer Differentialgleichung kann vektorwertig sein, das heißt, für jedes kann $y(t)=(y_{1}(t),\dotsc ,y_{d}(t))$ ein Vektor mit Komponenten sein. Man spricht dann auch von einem -dimensionalen Differentialgleichungssystem. Im Anschauungsfall eines bewegten Körpers ist dann y(t) seine Position im -dimensionalen euklidischen Raum und $y'(t)$ seine Geschwindigkeit zur Zeit . Durch die Differentialgleichung ist also in jedem Zeit- und Raumpunkt die Geschwindigkeit der gesuchten Bahnkurve mit Richtung und Betrag vorgegeben. Daraus soll die Bahn selbst berechnet werden.

Grundidee der Einschrittverfahren

Bei der oben als Beispiel betrachteten einfachen Differentialgleichung des exponentiellen Wachstums ließ sich die Lösungsfunktion direkt angeben. Das ist bei komplizierteren Problemen im Allgemeinen nicht mehr möglich. Man kann dann zwar unter gewissen Zusatzvoraussetzungen an die Funktion zeigen, dass eine eindeutig bestimmte Lösung des Anfangswertproblems existiert; diese kann aber dann nicht mehr durch Lösungsverfahren der Analysis (wie beispielsweise Trennung der Variablen, einen Exponentialansatz oder Variation der Konstanten) explizit berechnet werden. In diesem Fall können numerische Verfahren verwendet werden, um Näherungen für die gesuchte Lösung zu bestimmen.

Die Verfahren zur numerischen Lösung von Anfangswertproblemen gewöhnlicher Differentialgleichung lassen sich grob in zwei große Gruppen einteilen: die Einschritt- und die Mehrschrittverfahren. Beiden Gruppen ist gemeinsam, dass sie schrittweise Näherungen $y_{0},y_{1},y_{2},\dotsc$ für die gesuchten Funktionswerte $y(t_{0}),y(t_{1}),y(t_{2}),\dotsc$ an Stellen $t_{0}<t_{1}<t_{2}<\ldots$ berechnen. Die definierende Eigenschaft der Einschrittverfahren ist dabei, dass zur Bestimmung der folgenden Näherung $y_{{j+1}}$ nur die „aktuelle“ Näherung $y_{j}$ verwendet wird. Bei Mehrschrittverfahren gehen im Gegensatz dazu zusätzlich bereits zuvor berechnete Näherungen mit ein; ein Dreischrittverfahren würde also beispielsweise außer $y_{j}$ auch noch $y_{j-1}$ und $y_{j-2}$ zur Bestimmung der neuen Näherung $y_{{j+1}}$ verwenden.

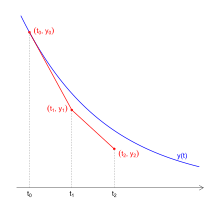
Zwei Schritte des expliziten Euler-Verfahrens

Das einfachste und grundlegendste Einschrittverfahren ist das explizite Euler-Verfahren, das der Schweizer Mathematiker und Physiker Leonhard Euler 1768 in seinem Lehrbuch Institutiones Calculi Integralis vorstellte. Die Idee dieser Methode ist es, die gesuchte Lösung durch eine stückweise lineare Funktion anzunähern, bei der in jedem Schritt von der Stelle $t_{j}$ zur Stelle $t_{j+1}$ die Steigung des Geradenstücks durch $f(t_{j},y_{j})$ gegeben ist. Genauer betrachtet: Durch die Problemstellung ist bereits ein Wert der gesuchten Funktion gegeben, nämlich $y(t_{0})=y_{0}$ . Aber auch die Ableitung an dieser Stelle ist bekannt, denn es gilt $y'(t_{0})=f(t_{0},y_{0})$ . Damit kann die Tangente an den Graphen der Lösungsfunktion bestimmt und als Näherung verwendet werden. An der Stelle $t_{1}>t_{0}$ ergibt sich mit der Schrittweite $h_{0}:=t_{1}-t_{0}$

$y(t_{1})\approx y_{0}+h_{0}f(t_{0},y_{0})=:y_{1}$ .

Dieses Vorgehen kann nun in den folgenden Schritten fortgesetzt werden. Insgesamt ergibt sich damit für das explizite Euler-Verfahren die Rechenvorschrift

$y_{j+1}=y_{j}+h_{j}f(t_{j},y_{j}),\quad j=0,1,2,\dotsc$

mit den Schrittweiten $h_{j}=t_{j+1}-t_{j}$ .

Das explizite Euler-Verfahren ist der Ausgangspunkt für zahlreiche Verallgemeinerungen, bei denen die Steigung $f(t_{j},y_{j})$ , durch Steigungen ersetzt wird, die das Verhalten der Lösung zwischen den Stellen $t_{j}$ und $t_{j+1}$ genauer annähern. Eine zusätzliche Idee für Einschrittverfahren bringt das implizite Eulerverfahren, das $f(t_{j+1},y_{j+1})$ als Steigung verwendet. Diese Wahl erscheint auf den ersten Blick wenig geeignet, da ja $y_{{j+1}}$ unbekannt ist. Als Verfahrensschritt erhält man aber nun die Gleichung

$y_{j+1}=y_{j}+h_{j}f(t_{j+1},y_{j+1})$

aus der $y_{{j+1}}$ (gegebenenfalls durch ein numerisches Verfahren) berechnet werden kann. Wählt man beispielsweise als Steigung das arithmetische Mittel aus den Steigungen des expliziten und des impliziten Euler-Verfahrens, so erhält man das implizite Trapez-Verfahren. Aus diesem lässt sich wiederum ein explizites Verfahren gewinnen, wenn man zum Beispiel das unbekannte $y_{{j+1}}$ auf der rechten Seite der Gleichung durch die Näherung des expliziten Euler-Verfahrens nähert, das sogenannte Heun-Verfahren. All diesen Verfahren und allen weiteren Verallgemeinerungen ist die Grundidee der Einschrittverfahren gemeinsam: der Schritt

$y_{j+1}=y_{j}+h_{j}\Phi$

mit einer Steigung $\Phi$ , die von $t_{j}$ , $y_{j}$ und $h_{j}$ sowie (bei impliziten Verfahren) von $y_{{j+1}}$ abhängen kann.

Definition

Mit den Überlegungen aus dem Einführungsabschnitt dieses Artikels kann der Begriff des Einschrittverfahrens wie folgt definiert werden: Gesucht sei die Lösung des Anfangswertproblems

, $\quad y(t_{0})=y_{0}$ .

Dabei werde vorausgesetzt, dass die Lösung

$y\colon I\to \mathbb {R} ^{d}$

auf einem gegebenen Intervall $I=[t_{0},T]$ existiert und eindeutig bestimmt ist. Sind

$t_{0}<t_{1}<t_{2}<\ldots <t_{n}=T$

Zwischenstellen im Intervall und $h_{j}=t_{j+1}-t_{j}$ die zugehörigen Schrittweiten, dann heißt das durch

$y_{j+1}=y_{j}+h_{j}\Phi (t_{j},y_{j},y_{j+1},h_{j})$ , $\quad j=0,\dotsc ,n-1$

gegebene Verfahren Einschrittverfahren mit Verfahrensfunktion $\Phi$ . Wenn $\Phi$ nicht von $y_{{j+1}}$ abhängt, dann nennt man es explizites Einschrittverfahren. Anderenfalls muss in jedem Schritt eine Gleichung für $y_{{j+1}}$ gelöst werden, und das Verfahren wird implizit genannt.

Konsistenz und Konvergenz

Konvergenzordnung

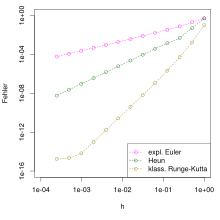
Globaler Fehler bei verschiedenen Schrittweiten für drei Einschrittverfahren. In doppelt-logarithmischer Auftragung erscheint der Zusammenhang jeweils ungefähr linear, die Steigungen entsprechen dabei den Konvergenzordnungen 1, 2 und 4.

Für ein praxistaugliches Einschrittverfahren sollen die berechneten $y_{j}$ gute Näherungen für die Werte $y(t_{j})$ der exakten Lösung an der Stelle $t_{j}$ sein. Da im Allgemeinen die Größen -dimensionale Vektoren sind, misst man die Güte dieser Näherung mit einer Vektornorm als $\|y_{j}-y(t_{j})\|$ , dem Fehler an der Stelle $t_{j}$ . Es ist wünschenswert, dass diese Fehler für alle schnell gegen null konvergieren, falls man die Schrittweiten gegen null konvergieren lässt. Um auch den Fall nicht konstanter Schrittweiten zu erfassen, definiert man dazu genauer als das Maximum der verwendeten Schrittweiten und betrachtet das Verhalten des maximalen Fehlers an allen Stellen $t_{j}$ im Vergleich zu Potenzen von . Man sagt, das Einschrittverfahren zur Lösung des gegebenen Anfangswertproblems habe die Konvergenzordnung $p\geq 1$ , wenn die Abschätzung

$\max _{j=0,\dotsc ,n}\|y_{j}-y(t_{j})\|\leq Ch^{p}$

für alle hinreichend kleinen mit einer von unabhängigen Konstante C>0 gilt.

Die Konvergenzordnung ist die wichtigste Kenngröße für den Vergleich verschiedener Einschrittverfahren. Ein Verfahren mit höherer Konvergenzordnung liefert im Allgemeinen bei vorgegebener Schrittweite einen kleineren Gesamtfehler bzw. umgekehrt sind weniger Schritte nötig, um eine vorgegebene Genauigkeit zu erreichen. Bei einem Verfahren mit p=1 ist zu erwarten, dass sich bei einer Halbierung der Schrittweite auch der Fehler nur ungefähr halbiert. Bei einem Verfahren der Konvergenzordnung p=4 kann man hingegen davon ausgehen, dass sich dabei der Fehler ungefähr um den Faktor ${\bigl (}{\tfrac {1}{2}}{\bigr )}^{4}={\tfrac {1}{16}}$ verringert.

Globaler und lokaler Fehler

Die in der Definition der Konvergenzordnung betrachteten Fehler $\|y_{j}-y(t_{j})\|$ setzen sich auf eine zunächst kompliziert erscheinende Weise aus zwei Einzelkomponenten zusammen: Natürlich hängen sie zum einen von dem Fehler ab, den das Verfahren in einem einzelnen Schritt macht, indem es die unbekannte Steigung der gesuchten Funktion durch die Verfahrensfunktion annähert. Zum anderen ist aber zusätzlich zu berücksichtigen, dass bereits der Startpunkt $(t_{j},y_{j})$ eines Schrittes im Allgemeinen nicht mit dem exakten Startpunkt $(t_{j},y(t_{j}))$ übereinstimmt; der Fehler nach diesem Schritt hängt also auch von allen Fehlern ab, die bereits in den vorangegangenen Schritten gemacht wurden. Aufgrund der einheitlichen Definition der Einschrittverfahren, die sich nur in der Wahl der Verfahrensfunktion $\Phi$ unterscheiden, lässt sich aber beweisen, dass man (unter gewissen technischen Voraussetzungen an $\Phi$ ) direkt von der Fehlerordnung in einem einzelnen Schritt, der sogenannten Konsistenzordnung, auf die Konvergenzordnung schließen kann.

Der Begriff der Konsistenz ist ein allgemeines und zentrales Konzept der modernen numerischen Mathematik. Während man bei der Konvergenz eines Verfahrens untersucht, wie gut die numerischen Näherungen zur exakten Lösung passen, stellt man sich bei der Konsistenz vereinfacht gesprochen die „umgekehrte“ Frage: Wie gut erfüllt die exakte Lösung die Verfahrensvorschrift? In dieser allgemeinen Theorie gilt, dass ein Verfahren genau dann konvergent ist, wenn es konsistent und stabil ist. Um die Notation zu vereinfachen, soll in der folgenden Überlegung angenommen werden, dass ein explizites Einschrittverfahren

$y_{j+1}=y_{j}+h\Phi (t_{j},y_{j},h)$

mit konstanter Schrittweite vorliegt. Mit der wahren Lösung $t\mapsto y(t)$ definiert man den lokalen Abschneidefehler (auch lokaler Verfahrensfehler genannt) $\eta$ als

$\eta (t,h)=y(t)+h\Phi (t,y(t),h)-y(t+h)$ .

Man nimmt also an, dass die exakte Lösung bekannt ist, startet einen Verfahrensschritt an der Stelle (t,y(t)) und bildet die Differenz zu exakten Lösung an der Stelle $t+h$ . Damit definiert man: Ein Einschrittverfahren hat die Konsistenzordnung $p\geq 1$ , wenn die Abschätzung

$\|\eta (t,h)\|\leq Ch^{p+1}$

für alle hinreichend kleinen mit einer von unabhängigen Konstante C>0 gilt.

Der auffällige Unterschied zwischen den Definitionen der Konsistenzordnung und der Konvergenzordnung ist die Potenz $h^{p+1}$ anstelle von $h^{p}$ . Das lässt sich anschaulich so deuten, dass beim Übergang vom lokalen zum globalen Fehler eine Potenz der Schrittweite „verloren geht“. Es gilt nämlich der folgende, für die Theorie der Einschrittverfahren zentrale Satz:

Ist die Verfahrensfunktion $\Phi$ Lipschitz-stetig und hat das zugehörige Einschrittverfahren die Konsistenzordnung , dann hat es auch die Konvergenzordnung .

Die Lipschitz-Stetigkeit der Verfahrensfunktion als Zusatzvoraussetzung für die Stabilität ist im Allgemeinen immer dann erfüllt, wenn die Funktion aus der Differentialgleichung selbst Lipschitz-stetig ist. Diese Forderung muss für die meisten Anwendungen sowieso vorausgesetzt werden, um die eindeutige Lösbarkeit des Anfangswertproblems zu garantieren. Nach dem Satz genügt es also, die Konsistenzordnung eines Einschrittverfahrens zu bestimmen. Das lässt sich prinzipiell durch Taylor-Entwicklung von $\eta (t,h)$ nach Potenzen von erreichen. In der Praxis werden die entstehenden Formeln für höhere Ordnungen sehr kompliziert und unübersichtlich, sodass zusätzliche Konzepte und Notationen benötigt werden.

Steifheit und A-Stabilität

→ Hauptartikel: Steifes Anfangswertproblem und A-Stabilität

Die Konvergenzordnung eines Verfahrens ist eine asymptotische Aussage, die das Verhalten der Näherungen beschreibt, wenn die Schrittweite gegen null konvergiert. Sie sagt jedoch nichts darüber aus, ob das Verfahren für eine gegebene feste Schrittweite auch tatsächlich eine brauchbare Näherung berechnet. Dass dies bei bestimmten Typen von Anfangswertproblemen tatsächlich ein großes Problem darstellen kann, beschrieben zuerst Charles Francis Curtiss und Joseph O. Hirschfelder 1952. Sie hatten beobachtet, dass bei manchen Differentialgleichungssystemen der chemischen Reaktionskinetik die Lösungen nicht mit expliziten numerischen Verfahren berechnet werden können, und nannten solche Anfangswertprobleme „steif“. Es existieren zahlreiche mathematische Kriterien, um für ein gegebenes Problem festzustellen, wie steif es ist. Anschaulich handelt es sich bei steifen Anfangswertproblemen meist um Differentialgleichungssysteme, bei denen einige Komponenten sehr schnell konstant werden, während andere Komponenten sich nur langsam ändern. Ein solches Verhalten tritt typischerweise bei der Modellierung chemischer Reaktionen auf. Die für die praktische Anwendung nützlichste Definition von Steifheit ist dabei jedoch: Ein Anfangswertproblem ist steif, wenn man bei seiner Lösung mit expliziten Einschrittverfahren die Schrittweite „zu klein“ wählen müsste, um eine brauchbare Lösung zu erhalten. Solche Probleme können also nur mit impliziten Verfahren gelöst werden.

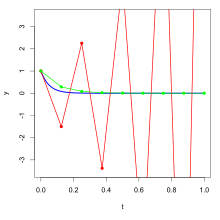
Zur Berechnung einer exponentiell fallenden Lösung (blau) ist das explizite Euler-Verfahren (rot) bei zu großer Schrittweite völlig unbrauchbar; das implizite Euler-Verfahren (grün) bestimmt die Lösung für beliebige Schrittweiten qualitativ richtig.

Dieser Effekt lässt sich genauer darstellen, wenn man untersucht, wie die einzelnen Verfahren mit exponentiellem Zerfall zurechtkommen. Dazu betrachtet man nach dem schwedischen Mathematiker Germund Dahlquist die Testgleichung

$y'(t)=\lambda y(t),\quad y(0)=1$

mit der für $\lambda <0$ exponentiell abfallenden Lösung $y(t)=e^{\lambda t}$ . Die nebenstehende Grafik zeigt – exemplarisch für das explizite und das implizite Euler-Verfahren – das typische Verhalten dieser beiden Verfahrensgruppen bei diesem so einfach erscheinenden Anfangswertproblem: Verwendet man bei einem expliziten Verfahren eine zu große Schrittweite, dann ergeben sich stark oszillierende Werte, die sich im Laufe der Rechnung aufschaukeln und sich immer weiter von der exakten Lösung entfernen. Implizite Verfahren berechnen hingegen typischerweise die Lösung für beliebige Schrittweiten qualitativ richtig, nämlich als exponentiell fallende Folge von Näherungswerten.

Etwas allgemeiner betrachtet man die obige Testgleichung auch für komplexe Werte von $\lambda$ . In diesem Fall sind die Lösungen Schwingungen, deren Amplitude genau dann beschränkt bleibt, wenn $\operatorname {Re} (\lambda )\leq 0$ gilt, also der Realteil von $\lambda$ kleiner oder gleich 0 ist. Damit lässt sich eine wünschenswerte Eigenschaft von Einschrittverfahren formulieren, die für steife Anfangswertprobleme eingesetzt werden sollen: die sogenannte A-Stabilität. Ein Verfahren heißt A-stabil, wenn es für beliebige Schrittweiten h>0 angewendet auf die Testgleichung für alle $\lambda$ mit $\operatorname {Re} (\lambda )\leq 0$ eine Folge von Näherungen $y_{0},y_{1},y_{2},\dotsc$ berechnet, die (wie die wahre Lösung) beschränkt bleibt. Das implizite Euler-Verfahren und das implizite Trapez-Verfahren sind die einfachsten Beispiele A-stabiler Einschrittverfahren. Andererseits lässt sich zeigen, dass ein explizites Verfahren niemals A-stabil sein kann.

Spezielle Verfahren und Verfahrensklassen

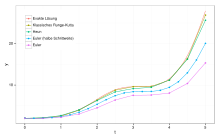
Einige Einschrittverfahren im Vergleich

Einfache Verfahren der Ordnung 1 und 2

Wie der französische Mathematiker Augustin-Louis Cauchy um 1820 bewies, besitzt das Euler-Verfahren die Konvergenzordnung 1. Wenn man die Steigungen $f(t_{j},y_{j})$ des expliziten Euler-Verfahrens und $f(t_{j+1},y_{j+1})$ des impliziten Euler-Verfahrens, wie sie an den beiden Endpunkten eines Schritts vorliegen, mittelt, kann man hoffen, eine bessere Näherung über das ganze Intervall zu erhalten. Tatsächlich lässt sich beweisen, dass das so erhaltene implizite Trapez-Verfahren

$y_{j+1}=y_{j}+{\frac {h}{2}}{\Big (}f(t_{j},y_{j})+f(t_{j+1},y_{j+1}){\Big )}$

die Konvergenzordnung 2 hat. Dieses Verfahren weist sehr gute Stabilitätseigenschaften auf, ist allerdings implizit, sodass in jedem Schritt eine Gleichung für $y_{{j+1}}$ gelöst werden muss. Nähert man diese Größe auf der rechten Seite der Gleichung durch das explizite Euler-Verfahren an, so entsteht das explizite Verfahren von Heun

$y_{j+1}=y_{j}+{\frac {h}{2}}{\Big (}f(t_{j},y_{j})+f{\big (}t_{j+1},y_{j}+hf(t_{j},y_{j}){\big )}{\Big )}$ ,

das ebenfalls die Konvergenzordnung 2 besitzt. Ein weiteres einfaches explizites Verfahren der Ordnung 2, das verbesserte Euler-Verfahren, erhält man durch folgende Überlegung: Eine „mittlere“ Steigung im Verfahrensschritt wäre die Steigung der Lösung in der Mitte des Schritts, also an der Stelle $t_{j}+{\tfrac {h}{2}}$ . Da die Lösung aber unbekannt ist, nähert man sie durch einen expliziten Euler-Schritt mit halber Schrittweite an. Es ergibt sich die Verfahrensvorschrift

$y_{j+1}=y_{j}+hf{\big (}t_{j}+{\tfrac {h}{2}},y_{j}+{\tfrac {h}{2}}f(t_{j},y_{j}){\big )}$ .

Diese Einschrittverfahren der Ordnung 2 wurden als Verbesserungen des Euler-Verfahrens alle 1895 von dem deutschen Mathematiker Carl Runge veröffentlicht.

Runge-Kutta-Verfahren

Das klassische Runge-Kutta-Verfahren vierter Ordnung mittelt in jedem Schritt vier Hilfssteigungen (rot)

→ Hauptartikel: Runge-Kutta-Verfahren

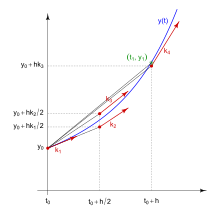
Die erwähnten Ideen für einfache Einschrittverfahren führen bei weiterer Verallgemeinerung zur wichtigen Klasse der Runge-Kutta-Verfahren. Zum Beispiel lässt sich das Verfahren von Heun übersichtlicher so präsentieren: Zuerst wird eine Hilfssteigung $k_{1}=f(t_{j},y_{j})$ berechnet, nämlich die Steigung des expliziten Euler-Verfahrens. Damit wird eine weitere Hilfssteigung bestimmt, hier $k_{2}=f(t_{j}+h,y_{j}+hk_{1})$ . Die tatsächlich verwendete Verfahrenssteigung $\Phi$ ergibt sich anschließend als ein gewichtetes Mittel der Hilfssteigungen, im Verfahren von Heun also ${\tfrac {1}{2}}k_{1}+{\tfrac {1}{2}}k_{2}$ . Dieses Vorgehen lässt sich auf mehr als zwei Hilfssteigungen verallgemeinern. Ein -stufiges Runge-Kutta-Verfahren berechnet zunächst Hilfssteigungen $k_{1},\dotsc ,k_{s}$ durch Auswertung von an geeigneten Stellen und anschließend $\Phi$ als gewichtetes Mittel. Bei einem expliziten Runge-Kutta-Verfahren werden die Hilfssteigungen $k_{1},k_{2},k_{3},\dotsc$ der Reihe nach direkt berechnet, bei einem impliziten ergeben sie sich als Lösungen eines Gleichungssystems. Als typisches Beispiel sei das explizite klassische Runge-Kutta-Verfahren der Ordnung 4 angeführt, das mitunter einfach als das Runge-Kutta-Verfahren bezeichnet wird: Dabei werden zunächst die vier Hilfssteigungen

${\begin{aligned}k_{1}&=f(t_{j},y_{j})\\k_{2}&=f(t_{j}+{\tfrac {h}{2}},y_{j}+{\tfrac {h}{2}}k_{1})\\k_{3}&=f(t_{j}+{\tfrac {h}{2}},y_{j}+{\tfrac {h}{2}}k_{2})\\k_{4}&=f(t_{j}+h,y_{j}+hk_{3})\end{aligned}}$

berechnet und dann als Verfahrenssteigung das gewichtete Mittel

${\tfrac {1}{6}}k_{1}+{\tfrac {1}{3}}k_{2}+{\tfrac {1}{3}}k_{3}+{\tfrac {1}{6}}k_{4}$

verwendet. Dieses bekannte Verfahren veröffentlichte der deutsche Mathematiker Wilhelm Kutta im Jahr 1901, nachdem ein Jahr zuvor Karl Heun ein dreistufiges Einschrittverfahren der Ordnung 3 gefunden hatte.

Die Konstruktion von expliziten Verfahren noch höherer Ordnung mit möglichst kleiner Stufenzahl ist ein mathematisch recht anspruchsvolles Problem. Wie John C. Butcher 1965 zeigen konnte, gibt es zum Beispiel für die Ordnung 5 nur minimal sechsstufige Verfahren; ein explizites Runge-Kutta-Verfahren der Ordnung 8 benötigt mindestens 11 Stufen. 1978 fand der österreichische Mathematiker Ernst Hairer ein Verfahren der Ordnung 10 mit 17 Stufen. Die Koeffizienten für ein solches Verfahren müssen 1205 Bestimmungsgleichungen erfüllen. Bei impliziten Runge-Kutta-Verfahren ist die Situation einfacher und übersichtlicher: Für jede Stufenzahl existiert ein Verfahren der Ordnung $p=2s$ ; das ist zugleich die maximal erreichbare Ordnung.

Extrapolationsverfahren

Die Idee der Extrapolation ist nicht auf die Lösung von Anfangswertproblemen mit Einschrittverfahren beschränkt, sondern lässt sich sinngemäß auf alle numerischen Verfahren anwenden, die das zu lösende Problem mit einer Schrittweite diskretisieren. Ein bekanntes Beispiel eines Extrapolationsverfahrens ist etwa die Romberg-Integration zur numerischen Berechnung von Integralen. Sei daher ganz allgemein ein Wert, der numerisch bestimmt werden soll, im Fall dieses Artikels etwa der Wert der Lösungsfunktion eines Anfangswertproblems an einer gegebenen Stelle. Ein numerisches Verfahren, beispielsweise ein Einschrittverfahren, berechnet dafür einen Näherungswert ${\tilde {v}}(h)$ , der von der Wahl der Schrittweite h>0 abhängt. Dabei sei angenommen, dass das Verfahren konvergent ist, also, dass ${\tilde {v}}(h)$ gegen konvergiert, wenn gegen null konvergiert. Diese Konvergenz ist jedoch nur eine rein theoretische Aussage, da bei der realen Anwendung des Verfahrens zwar Näherungswerte ${\tilde {v}}(h_{1}),{\tilde {v}}(h_{2}),\dotsc ,{\tilde {v}}(h_{m})$ für endlich viele verschiedene Schrittweiten $h_{1}>h_{2}>\ldots >h_{m}$ berechnet werden können, man aber selbstverständlich nicht die Schrittweite „gegen null konvergieren“ lassen kann. Die berechneten Näherungen für verschiedene Schrittweiten lassen sich jedoch als Information über die (unbekannte) Funktion $\tilde v$ auffassen: Bei den Extrapolationsverfahren wird dabei $\tilde v$ durch ein Interpolationspolynom angenähert, also durch ein Polynom mit

$P(h_{k})={\tilde {v}}(h_{k})$

für $k=1,2,\dotsc ,m$ . Der Wert P(0) des Polynoms an der Stelle h=0 wird dann als berechenbare Näherung für den nicht berechenbaren Grenzwert von ${\tilde {v}}(h)$ für gegen null verwendet. Einen frühen erfolgreichen Extrapolationsalgorithmus für Anfangswertprobleme veröffentlichten Roland Bulirsch und Josef Stoer im Jahr 1966.

Extrapolation auf

bei einem Verfahren der Ordnung

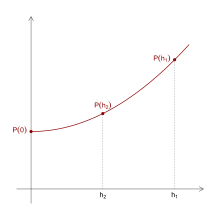
Ein konkretes Beispiel im Falle eines Einschrittverfahrens der Ordnung kann das allgemeine Vorgehen der Extrapolation verständlich machen. Bei einem solchen Verfahren lässt sich die berechnete Näherung für kleine Schrittweiten gut durch ein Polynom der Form

$P(h)=a+bh^{p}$

mit zunächst unbekannten Parametern und annähern. Berechnet man nun mit dem Verfahren für eine Schrittweite $h_{1}$ und für die halbe Schrittweite $h_{2}={\tfrac {1}{2}}h_{1}$ zwei Näherungen $y_{h_{1}}$ und $y_{h_{2}}$ , erhält man aus den Interpolationsbedingungen $P(h_{1})=y_{h_{1}}$ und $P(h_{2})=y_{h_{2}}$ zwei lineare Gleichungen für die Unbekannten und . Der auf h=0 extrapolierte Wert

$P(0)=a=y_{h_{2}}+{\frac {y_{h_{2}}-y_{h_{1}}}{2^{p}-1}}$

stellt dann im Allgemeinen eine deutlich bessere Näherung dar als die beiden zunächst berechneten Werte. Es lässt sich zeigen, dass die Ordnung des so erhaltenen Einschrittverfahrens mindestens p+1 ist, also um mindestens 1 größer als beim ursprünglichen Verfahren ist.

Verfahren mit Schrittweitensteuerung

→ Hauptartikel: Schrittweitensteuerung

Ein Vorteil der Einschrittverfahren ist, dass in jedem Schritt unabhängig von den anderen Schritten eine beliebige Schrittweite $h_{j}$ verwendet werden kann. In der Praxis stellt sich dabei offensichtlich die Frage, wie $h_{j}$ gewählt werden soll. In realen Anwendungen wird stets eine Fehlertoleranz gegeben sein, mit der die Lösung eines Anfangswertproblems berechnet werden soll; zum Beispiel wäre es sinnlos, eine numerische Näherung zu bestimmen, die wesentlich „genauer“ ist als die mit Messabweichungen behafteten Daten für Startwerte und Parameter des gegebenen Problems. Das Ziel wird also sein, die Schrittweiten so zu wählen, dass einerseits die vorgegebenen Fehlertoleranzen eingehalten werden, andererseits aber auch möglichst wenige Schritte zu verwenden, um den Rechenaufwand klein zu halten. Dies wird sich im Allgemeinen nur dann erreichen lassen, wenn die Schrittweiten an den Verlauf der Lösung angepasst werden: kleine Schritte, wo sich die Lösung stark ändert, große Schritte, wo sie nahezu konstant verläuft.

Bei gut konditionierten Anfangswertproblemen lässt sich zeigen, dass der globale Verfahrensfehler ungefähr gleich der Summe der lokalen Abschneidefehler $\eta _{j}:=\|\eta (t_{j},h_{j})\|$ in den einzelnen Schritten ist. Daher sollte als Schrittweite ein möglichst großes $h_{j}$ gewählt werden, für das $\eta _{j}$ unter einer gewählten Toleranzschwelle liegt. Das Problem dabei ist, dass $\eta _{j}$ nicht direkt berechnet werden kann, da es ja von der unbekannten exakten Lösung $y(t_{j})$ des Anfangswertproblems an der Stelle $t_{j}$ abhängt. Die Grundidee der Schrittweitensteuerung ist es daher, $y(t_{j})$ mit einem Verfahren anzunähern, das genauer ist als das zugrundeliegende Basisverfahren.

Zwei grundlegende Ideen zur Schrittweitensteuerung sind die Schrittweitenhalbierung und die eingebetteten Verfahren. Bei der Schrittweitenhalbierung wird zusätzlich zum eigentlichen Verfahrensschritt als Vergleichswert das Ergebnis für zwei Schritte mit der halben Schrittweite berechnet. Aus beiden Werten wird dann durch Extrapolation eine genauere Näherung für $y(t_{j})$ bestimmt und damit der lokale Fehler $\eta _{j}$ geschätzt. Ist dieser zu groß, wird dieser Schritt verworfen und mit einer kleineren Schrittweite wiederholt. Ist er deutlich kleiner als die vorgegebene Toleranz, kann im nächsten Schritt die Schrittweite vergrößert werden. Der zusätzliche Rechenaufwand für dieses Schrittweitenhalbierungsverfahren ist relativ groß; deshalb verwenden moderne Implementierungen meist sogenannte eingebettete Verfahren zur Schrittweitensteuerung. Die Grundidee ist dabei, in jedem Schritt zwei Näherungen für $y(t_{j})$ mit zwei Einschrittverfahren zu berechnen, die verschiedene Konvergenzordnungen haben, und damit den lokalen Fehler zu schätzen. Um den Rechenaufwand zu optimieren, sollten die beiden Verfahren möglichst viele Rechenschritte gemeinsam haben: Sie sollten „ineinander eingebettet“ sein. Eingebettete Runge-Kutta-Verfahren verwenden beispielsweise die gleichen Hilfssteigungen und unterscheiden sich nur darin, wie sie diese mitteln. Bekannte eingebettete Verfahren sind unter anderem die Runge-Kutta-Fehlberg-Verfahren (Erwin Fehlberg, 1969) und die Dormand-Prince-Verfahren (J. R. Dormand und P. J. Prince, 1980).

Praxisbeispiel: Lösen von Anfangswertproblemen mit numerischer Software

Für die in diesem Artikel überblicksartig dargestellten mathematischen Konzepte wurden zahlreiche Software-Implementierungen entwickelt, die dem Anwender die Möglichkeit geben, praktische Probleme auf einfache Weise numerisch zu lösen. Als konkretes Beispiel dazu soll nun eine Lösung der Lotka-Volterra-Gleichungen mit der verbreiteten numerischen Software Matlab berechnet werden. Die Lotka-Volterra-Gleichungen sind ein einfaches Modell aus der Biologie, das die Wechselwirkungen von Räuber- und Beutepopulationen beschreibt. Gegeben sei dazu das Differentialgleichungssystem

${\begin{aligned}y_{1}'(t)&=ay_{1}(t)-by_{1}(t)y_{2}(t)\\y_{2}'(t)&=cy_{1}(t)y_{2}(t)-dy_{2}(t)\end{aligned}}$

mit den Parametern $a=1,b=2,c=1,d=1$ und der Anfangsbedingung $y_{1}(0)=3$ , $y_{2}(0)=1$ . Hierbei entsprechen y_1 und y_2 der zeitlichen Entwicklung der Beute- bzw. der Räuberpopulation. Die Lösung soll auf dem Zeitintervall $[0,20]$ berechnet werden.

Für die Berechnung mithilfe von Matlab wird zunächst für die gegebenen Parameterwerte die Funktion auf der rechten Seite der Differentialgleichung $y'=f(t,y)$ definiert:

a = 1; b = 2; c = 1; d = 1;
f = @(t,y) [a*y(1) - b*y(1)*y(2); c*y(1)*y(2) - d*y(2)];

Außerdem werden das Zeitintervall und die Anfangswerte benötigt:

t_int = [0, 20];
y0 = [3; 1];

Anschließend kann die Lösung berechnet werden:

[t, y] = ode45(f, t_int, y0);

Die Matlab-Funktion ode45 implementiert ein Einschrittverfahren, das zwei eingebettete explizite Runge-Kutta-Verfahren mit den Konvergenzordnungen 4 und 5 zur Schrittweitensteuerung verwendet.

Die Lösung kann nun gezeichnet werden, y_1 als blaue Kurve und y_2 als rote; die berechneten Punkte werden durch kleine Kreise markiert:

figure(1)
plot(t, y(:,1), 'b-o', t, y(:,2), 'r-o')

Das Ergebnis ist unten im linken Bild dargestellt. Das rechte Bild zeigt die vom Verfahren verwendeten Schrittweiten und wurde erzeugt mit

figure(2)
plot(t(1:end-1), diff(t))

Lösungen der Lotka-Volterra-Gleichungen

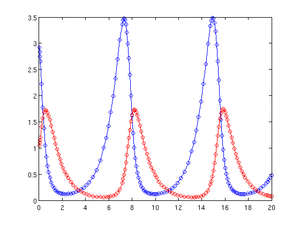
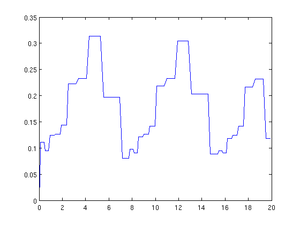
Lotka-Volterra equations ode45 stepsizes.png

Verwendete Schrittweiten

Dieses Beispiel kann ohne Änderungen auch mit der freien numerischen Software GNU Octave ausgeführt werden. Mit dem dort implementierten Verfahren ergibt sich allerdings eine etwas andere Schrittweitenfolge.

Basierend auf einem Artikel in:

Wikipedia.de