Polynominterpolation

Interpolationspolynom 7. Grades

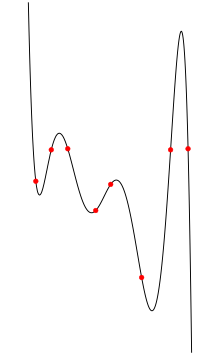
In der numerischen Mathematik versteht man unter Polynominterpolation die Suche nach einem Polynom, welches exakt durch vorgegebene Punkte (z.B. aus einer Messreihe) verläuft. Dieses Polynom wird Interpolationspolynom genannt und man sagt, es interpoliere die gegebenen Punkte.

Anwendungen

Polynome lassen sich sehr leicht integrieren und ableiten. Deswegen tauchen interpolierende Polynome an vielen Stellen in der numerischen Mathematik auf, beispielsweise bei der numerischen Integration und entsprechend bei Verfahren zur numerischen Lösung gewöhnlicher Differentialgleichungen.

Problemstellung

Für n+1 gegebene Wertepaare $(x_i,\,f_i)$ mit paarweise verschiedenen Stützstellen $x_{i}$ wird ein Polynom maximal -ten Grades gesucht, das alle Gleichungen

$P(x_i) = f_i, \quad i=0,\dotsc,n$

erfüllt. Ein solches Polynom existiert stets und ist eindeutig bestimmt, wie im Folgenden gezeigt wird.

Beim Interpolationsproblem ist also im Vektorraum $\Pi_n$ der Polynome mit Grad oder kleiner zu suchen, kurz $P \in \Pi_n$ . Ist $\phi_0,\dotsc,\phi_n$ eine Basis von $\Pi_n$ , so ergeben die Gleichungen P(x_i) = f_i ein lineares Gleichungssystem für die Koeffizienten der Basisdarstellung $P = \sum_{k=0}^n a_k \phi_k$ . Da sich ein und dasselbe Polynom aber unterschiedlich darstellen lässt, je nachdem welche Basis für den Vektorraum $\Pi_n$ gewählt wird, kann man ganz verschiedene Gleichungssysteme erhalten. Wählt man für $\Pi_n$ die Standardbasis $\left\{x^k\mid 0\le k\le n\right\}$ , also für die Darstellung $P(x) = \sum_{k=0}^n a_kx^k$ , so erhält man ein Gleichungssystem mit der Vandermonde-Matrix:

$\begin{pmatrix} 1 & x_0 & \cdots & x_0^n \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_n & \cdots & x_n^n \end{pmatrix} \begin{pmatrix} a_0 \\ \vdots \\ a_n \end{pmatrix} = \begin{pmatrix} f_0 \\ \vdots \\ f_n \end{pmatrix}$ .

Diese ist regulär, wenn die Stützstellen $x_{i}$ paarweise verschieden sind, das Gleichungssystem lässt sich dann eindeutig lösen. Somit ist die Existenz und Eindeutigkeit des gesuchten Polynoms $P \in \Pi_n$ immer sichergestellt. Trotz der theoretischen Machbarkeit wird diese Art der Interpolation in der Praxis nicht durchgeführt, da die Berechnung der Vandermonde-Matrix aufwendig ist ( $\mathcal O(n^2)$ , siehe Landau-Symbole) und zudem schlecht konditioniert bei einer ungeeigneten Wahl der Stützstellen.

Lösungsverfahren

Obiges Gleichungssystem ließe sich beispielsweise mit dem Gaußschen Eliminationsverfahren lösen. Der Aufwand dafür ist mit ${\mathcal {O}}(n^{3})$ allerdings vergleichsweise groß. Bei Wahl einer anderen Basis als der Standardbasis zur Beschreibung des Polynoms kann der Aufwand verringert werden.

Lagrangesche Interpolationsformel

Beispielhafte lagrangesche Basisfunktionen für x₀ = 0, x₁ = 1, x₂ = 2, x₃ = 3 (n = 3)

Eher für theoretische Betrachtungen günstig ist eine Darstellung in der Lagrange-Basis. Die Basisfunktionen sind die Lagrange-Polynome

$\ell _{i}(x)=\prod _{\begin{smallmatrix}j=0\\j\neq i\end{smallmatrix}}^{n}{\frac {x-x_{j}}{x_{i}-x_{j}}}={\frac {x-x_{0}}{x_{i}-x_{0}}}\cdots {\frac {x-x_{i-1}}{x_{i}-x_{i-1}}}\cdot {\frac {x-x_{i+1}}{x_{i}-x_{i+1}}}\cdots {\frac {x-x_{n}}{x_{i}-x_{n}}}\,,$

die so definiert sind, dass

$\ell_i(x_k) = \delta_{ik} = \left\{\begin{matrix} 1 & \mbox{falls } i=k \\ 0 & \mbox{falls } i \neq k \end{matrix}\right.$

gilt, wobei $\delta_{ik}$ das Kronecker-Delta darstellt. Damit entspricht die Matrix $\left(\ell_i\left(x_j\right)\right)_{i,j=0,1,\ldots,n}$ genau der Einheitsmatrix. Die Lösung des Interpolationsproblems lässt sich dann einfach angeben als

$P(x) = \sum_{i=0}^n f_i\ell_i\left(x\right)$

mit den Stützwerten $f_{i}$ . Dies wird häufig benutzt, um die Existenz der Lösung des Interpolationsproblems zu beweisen. Ein Vorteil der Lagrange-Basis ist somit, dass die Basisfunktionen $\ell_i$ von den Stützwerten $f_{i}$ unabhängig sind. Dadurch lassen sich verschiedene Sätze von Stützwerten $f_{i}$ mit gleichen Stützstellen $x_{i}$ schnell interpolieren, wenn die Basisfunktionen $\ell_i$ einmal bestimmt worden sind. Ein Nachteil dieser Darstellung ist jedoch, dass alle Basisvektoren bei Hinzunahme einer einzelnen Stützstelle komplett neu berechnet werden müssen, weshalb dieses Verfahren für die meisten praktischen Zwecke zu aufwendig ist.

Baryzentrische Interpolationsformel

Die Lagrangesche Interpolationsformel kann umgeformt werden in die praktisch relevantere Baryzentrische Interpolationsformel

$P(x)={\frac {\sum _{j=0}^{n}{\frac {\lambda _{j}f_{j}}{x-x_{j}}}}{\sum _{j=0}^{n}{\frac {\lambda _{j}}{x-x_{j}}}}}\,,$

wobei die Baryzentrischen Gewichte wie folgt definiert sind

$\lambda _{j}:=\prod _{\begin{smallmatrix}i=0\\i\neq j\end{smallmatrix}}^{n}{\frac {1}{x_{j}-x_{i}}}\,.$

Für vorgegebene Stützstellen $(x_{i})_{i}$ können die Gewichte $(\lambda _{i})_{i}$ vorberechnet werden, sodass der Aufwand für die Auswertung von P(x) nur noch bei ${\mathcal {O}}(n)$ liegt. Beim Hinzufügen einer neuen Stützstelle müssen die Gewichte neubestimmt werden. Dies hat einen Aufwand von ${\mathcal {O}}(n)$ im Vergleich zum Neubestimmen der Lagrangepolynome von ${\mathcal {O}}(n^{2})$ .

Newtonscher Algorithmus

In diesem Verfahren wird das Polynom in Newton-Basis dargestellt, so dass die Koeffizienten effizient mit dem Schema der dividierten Differenzen bestimmt werden können. Eine effiziente Auswertung des Polynoms kann dann mithilfe des Horner-Schemas erfolgen.

Ansatz: Newton-Basis

Als Ansatz für das gesuchte Interpolationspolynom wählt man die Newton-Basisfunktionen N_0(x)=1 und $\textstyle N_i(x) = \prod_{j=0}^{i-1}\left(x-x_j\right)=\left(x-x_0\right)\cdots\left(x-x_{i-1}\right)$ mit $i=1,\ldots ,n$ , so dass dargestellt wird mit der Newtonschen Interpolationsformel

$P(x)=\sum_{i=0}^n c_i\cdot N_i(x)=c_0+c_1 \left(x-x_0\right)+c_2 \left(x-x_0\right) \left(x-x_1\right)+\dotsb+c_n\left(x-x_0\right)\dotsm \left(x-x_{n-1}\right)$

Das Gleichungssystem der Gleichungen P(x_i) = f_i hat dann die Form

$\begin{pmatrix} 1 & & & & 0 \\ 1 & (x_1 - x_0) & & & \\ 1 & (x_2 - x_0) & (x_2 - x_0)(x_2 - x_1) & & \\ \vdots & \vdots & & \ddots & \\ 1 & (x_n - x_0) & \cdots & & \prod_{i=0}^{n-1}(x_n - x_i) \\ \end{pmatrix} \cdot \begin{pmatrix} c_0 \\ \vdots \\ c_n \end{pmatrix} = \begin{pmatrix} f_0 \\ \vdots \\ f_n \end{pmatrix}$

Im Gegensatz zur komplizierten Vandermonde-Matrix bei Wahl der Standardbasis $\{x^k|0 \le k \le n\}$ erhält man bei Wahl der Newton-Basis also eine einfach strukturierte untere Dreiecksmatrix und das Gleichungssystem lässt sich einfach lösen.

Bestimmung der Koeffizienten: Schema der dividierten Differenzen

Die Koeffizienten $c_{i}$ werden aber nicht direkt aus dem obigen Gleichungssystem bestimmt, sondern effizienter mithilfe der dividierten Differenzen. Durch Induktion beweist man mit der Rekursionsformel von Aitken, dass für die Koeffizienten $c_{i}$ gilt

$c_i = [x_0, \dotsb, x_i]f$ .

Dabei sind für i<j die dividierten Differenzen $[x_i, \dotsc, x_j]f$ rekursiv definiert durch

$[x_i]f = f_i \qquad$

$[x_i,\dotsc,x_j]f = \frac {[x_{i+1},\dotsc,x_j]f-[x_i,\dotsc,x_{j-1}]f}{x_j - x_i}$ .

Die Notation mit angehängtem erklärt sich dadurch, dass oft eine unbekannte Funktion angenommen wird, die bei bekannten Funktionswerten f_i = f(x_i) interpoliert werden soll.

Die rekursive Berechnung der dividierten Differenzen lässt sich wie folgt veranschaulichen. Dabei sind die gesuchten Koeffizienten $c_{i}$ genau die oberste Schrägzeile:

${\begin{array}{crcrccrcrc}[x_{0}]f\\&\searrow \\{}[x_{1}]f&\rightarrow &[x_{0},x_{1}]f\\&\searrow &&\searrow \\{}[x_{2}]f&\rightarrow &[x_{1},x_{2}]f&\rightarrow &[x_{0},x_{1},x_{2}]f\\{}\vdots &\vdots &\vdots &\vdots &\vdots &\ddots \\{}&\searrow &&\searrow &&&\searrow \\{}[x_{n-1}]f&\rightarrow &[x_{n-2},x_{n-1}]f&\rightarrow &[x_{n-3},x_{n-2},x_{n-1}]f&\cdots &\rightarrow &[x_{0}\ldots x_{n-1}]f\\&\searrow &&\searrow &&&\searrow &&\searrow \\{}[x_{n}]f&\rightarrow &[x_{n-1},x_{n}]f&\rightarrow &[x_{n-2},x_{n-1},x_{n}]f&\cdots &\rightarrow &[x_{1}\ldots x_{n}]f&\rightarrow &[x_{0}\ldots x_{n}]f\end{array}}$

Offensichtlich ist bei Ergänzung der n+1 Wertepaare (x_i, f_i) um einen weiteren Punkt $(x_{n+1}, f_{n+1})$ in obigem Schema nur eine weitere Zeile hinzuzufügen, um den zusätzlichen Koeffizienten $c_{n+1} = [x_0, \dotsc, x_{n+1}]f$ zu berechnen. Die zuvor bestimmten Koeffizienten $c_0, \dotsc, c_n$ müssen nicht neu berechnet werden.

Alternativ zur obigen rekursiven Definition wird zum Beispiel in einem der Artikel von Marsden die dividierte Differenz $[x_{0},\ldots ,x_{n}]f$ einer hinreichend oft differenzierbaren Funktion als der eindeutige Koeffizient zur höchsten Potenz von eines Polynoms -ten Grads p(x) definiert, das an den Stellen $x_{0},\ldots ,x_{n}$ interpoliert. Tritt dabei ein Wert in der Sequenz $x_{0},\ldots ,x_{n}$ mit der Vielfachheit $\nu \geq 1$ auf, so sollen die Ableitungen des Polynoms die Ableitungen der Funktion an dieser Stelle bis zur Ordnung $\nu -1$ interpolieren. Es gilt somit

$[x_{0},\dotsc ,x_{k}]f={\frac {f^{(k)}(x^{*})}{k!}}\qquad {\text{falls}}\quad x^{*}:=x_{0}=\ldots =x_{k}\,.$

Auswertung des Polynoms: Horner-Schema

Wenn die Koeffizienten $c_{i}$ des Interpolationspolynoms einmal bekannt sind, kann man es effizient mithilfe des Horner-Schemas auswerten. Dazu schreibt man in der Form (einfache Umformung der Newtonschen Interpolationsformel)

$P(x) = \left(\cdots\left(c_n(x - x_{n-1}\right) + c_{n-1})(x - x_{n-2}) + \dotsb + c_1\right)(x - x_0) + c_0$ ,

so dass P(x) rekursiv berechnet werden kann durch

$\begin{align} b_n & = c_n \\ b_i & = b_{i+1}(x - x_i) + c_i, \qquad i = n - 1, \dotsc, 0 \\ P(x) & = b_0 \end{align}$

Dies erfordert einen Aufwand von ${\mathcal {O}}(n)$ .

Algorithmus von Neville-Aitken

Ähnlich wie im Newtonschen Algorithmus wird beim Algorithmus von Neville-Aitken die Lösung rekursiv berechnet. Dazu bezeichne $p\left(f|x_i...x_{j}\right)$ das eindeutig bestimmte Interpolationspolynom -ten Grades zu den k+1 Stützpunkten $(x_{i}, f_{i}), \dots, (x_{j}, f_{j})$ , wobei k=j-i ist. Es gilt dann die Rekursionsformel von Aitken:

$\begin{align}p(f|x_i)(x) & \equiv f_i, \\ p(f|x_i, \dotsc, x_{j})(x) & \equiv \frac{(x - x_i)p(f|x_{i+1}, \dotsc, x_{j})(x) - (x - x_{j})p(f|x_{i}, \dotsc, x_{j-1})(x)}{x_{j}-x_{i}}.\end{align}$

Beweisen lässt sie sich durch Einsetzen von $x_{i}$ , wodurch man verifiziert, dass die rechte Seite der Gleichung die Interpolationsbedingung erfüllt. Die Eindeutigkeit des Interpolationspolynoms liefert dann die Behauptung.

Mit dem Schema von Neville kann die Auswertung von $p(f|{x_0, \dotsc, x_n})(x) = P(x)$ dann rekursiv erfolgen:

${\begin{array}{crcrccrcrc}p(f|x_{0})\\&\searrow \\p(f|x_{1})&\rightarrow &p(f|x_{0},x_{1})\\&\searrow &&\searrow \\p(f|x_{2})&\rightarrow &p(f|x_{1},x_{2})&\rightarrow &p(f|x_{0},x_{1},x_{2})\\\vdots &&\vdots &&\vdots &\ddots \\&\searrow &&\searrow &&&\searrow \\p(f|x_{n-1})&\rightarrow &p(f|x_{n-2},x_{n-1})&\rightarrow &p(f|x_{n-3},x_{n-2},x_{n-1})&\cdots &\rightarrow &p(f|x_{0},\dots ,x_{n-1})\\&\searrow &&\searrow &&&\searrow &&\searrow \\p(f|x_{n})&\rightarrow &p(f|x_{n-1},x_{n})&\rightarrow &p(f|x_{n-2},x_{n-1},x_{n})&\cdots &\rightarrow &p(f|x_{1},\dots ,x_{n})&\rightarrow &p(f|x_{0},\dots ,x_{n})\end{array}}$

Vergleich der Lösungsverfahren

Möchte man alle Koeffizienten des Interpolationspolynoms bestimmen, so bietet der Newtonsche Algorithmus hierfür den geringsten notwendigen Aufwand von $\mathcal O(n^2)$ . Das so bestimmte Polynom lässt sich dann mit ${\mathcal {O}}(n)$ Operationen an einer Stelle auswerten. Darum ist der Newtonsche Algorithmus gut geeignet, wenn das Interpolationspolynom an vielen Stellen ausgewertet werden soll. Auch lassen sich effizient weitere Stützpunkte hinzufügen. Liegen die Stützstellen oder die Stützwerte allerdings zu nahe beieinander, so besteht die Gefahr der Auslöschung bei der Bestimmung der dividierten Differenzen.

Der Neville-Aitken-Algorithmus ist dagegen gut geeignet, wenn ein Interpolationspolynom nur an ganz wenigen Stellen ausgewertet werden soll, dabei ist er weniger anfällig gegen Auslöschung. Auch im Neville-Aitken-Algorithmus lassen sich effizient neue Stützpunkte hinzufügen. So kann z.B. eine gewünschte Genauigkeit der Interpolation an einer Stelle durch Hinzufügen immer weiterer Stützstellen erreicht werden.

Beispiel: Interpolation der Tangensfunktion

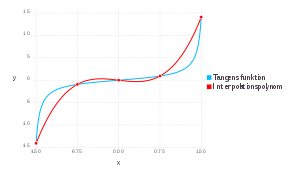
Tangensfunktion (blau) und ihre Polynominterpolante dritten Grades (rot)

Interpoliere die Funktion $f(x)=\tan(x)$ bei gegebenen Punkten

$x_0 = -1{,}5$	$f(x_0) = -14{,}101420$
$x_1 = -0{,}75$	$f(x_1) = -0{,}931596$

$x_3 = 0{,}75$	$f(x_3) = 0{,}931596$
$x_4 = 1{,}5$	$f(x_4) = 14{,}101420$

Lösung mit Lagrange

Die Lagrange-Basisfunktionen sind

$\begin{align} \ell_0(x)&={x - x_1 \over x_0 - x_1}\cdot{x - x_2 \over x_0 - x_2}\cdot{x - x_3 \over x_0 - x_3}\cdot{x - x_4 \over x_0 - x_4} ={1\over 243} x (2x-3)(4x-3)(4x+3)\\ \ell_1(x)&= {x - x_0 \over x_1 - x_0}\cdot{x - x_2 \over x_1 - x_2}\cdot{x - x_3 \over x_1 - x_3}\cdot{x - x_4 \over x_1 - x_4} =-{8\over 243} x (2x-3)(2x+3)(4x-3)\\ \ell_2(x)&={x - x_0 \over x_2 - x_0}\cdot{x - x_1 \over x_2 - x_1}\cdot{x - x_3 \over x_2 - x_3}\cdot{x - x_4 \over x_2 - x_4} ={3\over 243} (2x+3)(4x+3)(4x-3)(2x-3)\\ \ell_3(x)&={x - x_0 \over x_3 - x_0}\cdot{x - x_1 \over x_3 - x_1}\cdot{x - x_2 \over x_3 - x_2}\cdot{x - x_4 \over x_3 - x_4} =-{8\over 243} x (2x-3)(2x+3)(4x+3)\\ \ell_4(x)&={x - x_0 \over x_4 - x_0}\cdot{x - x_1 \over x_4 - x_1}\cdot{x - x_2 \over x_4 - x_2}\cdot{x - x_3 \over x_4 - x_3} ={1\over 243} x (2x+3)(4x-3)(4x+3) \end{align}$

also ist das Interpolationspolynom

${\begin{aligned}P_{\text{Lagrange}}(x)=&{\tfrac {1}{243}}{\big (}f(x_{0})x(2x-3)(4x-3)(4x+3)\\&\qquad {}-8f(x_{1})x(2x-3)(2x+3)(4x-3)\\&\qquad {}+3f(x_{2})(2x+3)(4x+3)(4x-3)(2x-3)\\&\qquad {}-8f(x_{3})x(2x-3)(2x+3)(4x+3)\\&\qquad {}+f(x_{4})x(2x+3)(4x-3)(4x+3){\big )}\\=&-1{,}477474x+4{,}834848x^{3}\end{aligned}}$

Lösung mit Newton

Die dividierten Differenzen sind hier

$\begin{array}{rrrrrr} x_i & f(x_i) & & & &\\ -1{,}50& -14{,}10140& & & &\\ & & & & &\\ -0{,}75& -0{,}931596&{-0{,}931596-(-14{,}1014) \over -0{,}75-(-1{,}5)}=17{,}5597& & &\\ & & & & &\\ 0{,}00 & 0{,}00000 &{0-(-0{,}931596) \over 0 - (-0{,}75)}=1{,}24213 &{1{,}24213-17{,}5597 \over 0-(-1{,}5) }=-10{,}8784& &\\ & & & & &\\ 0{,}75 & 0{,}931596 &{0{,}931596 - 0 \over 0{,}75-0}=1{,}24213 &{1{,}24213-1{,}24213 \over 0{,}75-(-0{,}75)}=0{,}00000 &{0 - (-10{,}8784) \over 0{,}75-(-1{,}5)}=4{,}83484&\\ & & & & &\\ 1{,}50 & 14{,}10140 &{14{,}10140-0{,}931596 \over 1{,}5 - 0{,}75}=17{,}5597 &{17{,}5597-1{,}24213 \over 1{,}5-0}=10{,}8784 &{10{,}8784-0 \over 1{,}5-(-0{,}75)}=4{,}83484 &{4{,}83484-4{,}83484 \over 1{,}5-(-1{,}5)}=0\\ \end{array}$

und das Interpolationspolynom ist

$\begin{align}P_\text{Newton}(x) =& -14{,}1014+17{,}5597(x+1{,}5)-10{,}8784(x+1{,}5)(x+0{,}75) \\ & {} +4{,}83484(x+1{,}5)(x+0{,}75)x+0(x+1{,}5)(x+0{,}75)x(x-0{,}75)\\ =& -0{,}00005-1{,}4775x-0{,}00001x^2+4{,}83484x^3\end{align}$

Verwendet man genauere Startwerte $f(x_{i})$ , verschwinden der erste und der dritte Koeffizient.

Interpolationsgüte

Fehlerabschätzung

Gegeben sei eine Funktion , deren n+1 Funktionswerte $f_{i}$ an den Stellen $x_{i}$ durch das Polynom interpoliert werden. Mit sei das kleinste Intervall bezeichnet, das die Stützstellen $x_{i}$ und eine Stelle enthält. Ferner sei ( n+1 )-mal stetig differenzierbar auf . Dann existiert ein $\xi \in I$ , für das gilt:

$f(x) - P(x) = \frac{f^{(n+1)}(\xi)}{(n+1)!} \prod_{i=0}^n (x-x_i)$

Insbesondere ist also bezüglich der Maximumsnorm auf [a,b] und mit $w_{n}(x)=\prod _{i=0}^{n}(x-x_{i})$ :

$|f(x)-P(x)|\leq {\frac {\|f^{(n+1)}\|_{\infty }}{(n+1)!}}\prod _{i=0}^{n}|x-x_{i}|\leq {\frac {\|f^{(n+1)}\|_{\infty }}{(n+1)!}}\|w_{n}\|_{\infty }$

Fehleroptimierung nach Tschebyschow

Für größere clustern die Tschebyschow-Punkte an den Intervallrändern.

Der Fehler hängt also von einer Ableitung von ab und von dem Produkt $w_n(x):=\prod_{i=0}^n (x-x_i)$ , also den Stützstellen $x_{i}$ . Manchmal ist man in der Position, dass man sich Stützstellen selbst wählen kann; etwa, wenn man ein physikalisches Experiment durchführt, oder aber auch bei einigen Verfahren zur numerischen Lösung von Differentialgleichungen. In diesem Fall ist die Frage interessant, für welche Stützstellen die Maximumsnorm $\|w_{n}\|_{\infty }$ minimal wird.

Für einen Beweis betrachten man normalerweise normierte Stützstellen

${\begin{aligned}w_{n}:[-1,1]\rightarrow \mathbb {R} ,\ w_{n}(x)=\prod _{i=0}^{n}(x-x_{i})\\{\text{mit}}\qquad \forall \,i=0,\ldots ,n:\quad x_{i}\in [-1,1]\,.\end{aligned}}$

Nun kann man die Maximumsnorm der Funktion w_n wie folgt abschätzen

$\|w_{n}\|_{[-1,1],\infty }=\max _{x\in [-1,1]}|w_{n}(x)|\geq 2^{-n}\,.$

Pafnuti Lwowitsch Tschebyschow hat gezeigt, dass die Nullstellen der Tschebyschow-Polynome („Tschebyschow-Punkte“) optimale Stützstellen sind. Die Polynome $T_{n+1}(x)=\cos((n+1) \arccos(x) )$ haben die Nullstellen $t_k=\cos\left(\frac{2k+1}{2n+2} \pi\right)$ für $k\in \{0,1,\ldots ,n\}$ . So gewählte Stützstellen liefern eine scharfe Grenze der oberen Abschätzung

$\|w_{n}\|_{[-1,1],\infty }=2^{-n}\,.$

Diese Aussage kann dann mit der Transformation

${\begin{aligned}\xi \in [-1,1]&\rightsquigarrow x={\frac {a+b}{2}}+{\frac {b-a}{2}}\xi &\in [a,b]\\x\in [a,b]&\rightsquigarrow \xi ={\frac {2x-a-b}{b-a}}&\in [-1,1]\end{aligned}}$

auf den Fall eines allgemeinen Intervalls $[a,b]\subset\mathbb{R}$ übertragen werden. Der Beweis liefert auch die Abschätzung

${\begin{aligned}\|w_{n}\|_{[a,b],\infty }=\max _{x\in [a,b]}|w_{n}(x)|=2\left({\frac {b-a}{4}}\right)^{n+1}.\end{aligned}}$

Runges Phänomen

Interpolation der Rungefunktion bei 6 äquidistanten Stützstellen (rote Punkte)

Interpolation der Rungefunktion bei 11 äquidistanten Stützstellen (rote Punkte)

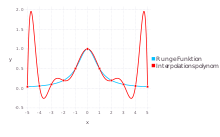
Verbessert sich die Interpolationsgüte, wenn mehr Stützpunkte hinzugefügt werden? Im Allgemeinen nicht: Bei hohem Grad des Polynoms kann es vorkommen, dass die Polynomfunktion kaum noch der zu interpolierenden Funktion ähnelt, was auch als Runges Phänomen bekannt ist. Polynome streben im Grenzfall $x\to \pm \infty$ gegen $\pm\infty$ . Verhält sich die zu interpolierende Funktion anders, etwa periodisch oder asymptotisch konstant, treten starke Oszillationen in der Nähe der Intervallgrenzen auf. Für solche Funktionen sind Polynominterpolationen über das gesamte Intervall relativ ungeeignet.

Tschebyschow-Stützstellen, die an den Intervallgrenzen dichter liegen, können zwar den Gesamtfehler der Interpolation verkleinern, dennoch empfiehlt sich ein Wechsel des Interpolationsverfahrens, etwa zur Spline-Interpolation. Runge gab für dieses Phänomen ein Beispiel an, die nach ihm benannte Runge-Funktion:

$f(x)=\frac{1}{1+x^2}\,,\quad x\in[-5;5]$

Konvergenzverhalten

Es gibt aber Bedingungen, unter denen sich die Interpolationsgüte mit steigender Anzahl von Stützpunkten verbessert: Wenn das Stützstellengitter immer „feiner“ wird und eine analytische Funktion interpoliert wird. Genauer: Sei eine analytische Funktion auf dem Intervall $I=[a,b] \subset \R$ . Für eine Intervallteilung

$\Delta_m = \{a=x_0^{(m)} < x_1^{(m)} < \dotsb < x_{n_m}^{(m)}=b\}, \qquad m\in \N$

sei ihre Norm definiert durch

$\|\Delta_m\| = \max_i|x_{i+1}^{(m)} - x_i^{(m)}|.$

Zu jeder Intervallteilung $\Delta_m$ gibt es ein eindeutig bestimmtes Polynom $P_{\Delta_m}$ , das an den Stützstellen $\Delta_m$ interpoliert. Gilt für eine Folge von Intervallteilungen $\|\Delta_m\| \rightarrow 0$ , so folgt $P_{\Delta_m} \rightarrow f$ gleichmäßig.

Allerdings lässt sich zu jeder Folge $\{\Delta_m\}_{m \in \N}$ auch eine auf stetige Funktion finden, so dass $\{P_{\Delta_m}\}_{m \in \N}$ nicht gleichmäßig gegen konvergiert (Satz von Faber).

Bestapproximation

Der Zusammenhang zwischen dem Interpolationpolynom und dem Polynom welches die Funktion am besten (bezüglich der Maximumsnorn $\|\cdot \|_{\max }$ ) annähert ist wie folgt.

Seien dazu folgende gegeben

eine stetige, zu nähernde Funktion: $f\in C([a,b])$
Stützstellen: $x_{0},\ldots ,x_{n}\in [a,b]$
Polynominterpolation#Lebesgue_Konstante: $\Lambda _{n}$
Interpolationspolynom: $P\in P_{n}$ mit $P(x_{i})=f(x_{i})$
Bestapproximation: $Q\in P_{n}$ mit $\|f-Q\|_{\max }=\min _{R\in P_{n}}\|f-R\|_{\max }$ .

Dann gilt die folgende Abschätzung

$\|f-P\|_{\max }=(1+\Lambda _{n})\|f-Q\|_{\max }\,.$

Verallgemeinerung

Bisher wurden die Stützstellen $x_{i}$ des Interpolationspolynoms als paarweise verschieden angenommen. Bei der Hermiteinterpolation ist das nicht der Fall. An mehrfach vorkommenden Stützstellen werden dabei nicht nur die Funktionswerte, sondern auch die Werte der Ableitungen des Interpolationspolynoms vorgegeben.

Lebesgue Konstante

Sei der Operator, der einer Funktion sein Interpolationspolynom $P(f)$ zuordnet, definiert durch

$\phi _{n}\colon C([a,b])\rightarrow P_{n}\,,\ f\mapsto P(f)=\sum _{i=0}^{n}f(x_{i})l_{i}\,,$

wobei l_i das -te Lagrange-Polynom ist.

Als Lebesgue Konstante $\Lambda _{n}$ wird die Operatornorm von $\phi _{n}$ bezeichnet. Dafür wird eine Norm benötigt und oft wird hier auf die Maximumsnorm $\|\cdot \|_{\max }$ zugegriffen

$\Lambda _{n}:=\|\phi _{n}\|_{\max }\,.$

Die Norm kann explizit evaluiert werden

$\Lambda _{n}=\max _{x\in [a,b]}\sum _{i=0}^{n}|L_{i}(x)|\,.$

Basierend auf einem Artikel in:

Wikipedia.de