
Spline-Interpolation

Bei der Spline-Interpolation versucht man, gegebene Stützstellen, auch Knoten genannt, mit Hilfe stückweiser Polynome niedrigen Grades zu interpolieren. Während das Ergebnis einer Polynominterpolation durch unvorteilhaft festgelegte Stützstellen oft bis zur Unkenntlichkeit oszilliert, liefert die Splineinterpolation brauchbare Kurvenverläufe und Approximationseigenschaften (Rungephänomen). Die Spline-Interpolation lässt sich mit geringem, linearem Aufwand berechnen, liefert aber im Vergleich zur Polynominterpolation eine geringere Konvergenzordnung.
Vorlage für die Splineinterpolation (dritten Grades) ist das traditionelle, biegsame Lineal der Schiffbauer, die Straklatte (englisch Spline). Diese wird an beliebig vielen, vom Konstrukteur vorgegebenen Punkten fixiert und verbindet die Punkte dann durch eine glatte und harmonische Biegelinie. Die Straklatte erzeugt so die Linie durch alle Punkte mit minimaler Biegeenergie und kleinsten Krümmungen. Während bei der Straklatte die Wendestellen (Orte maximaler Linearität und minimaler Biegeenergie) in der Regel zwischen den Stützstellen liegen und die Stützstellen selbst Orte maximaler Krümmung sind (Orte maximaler Kraft durch Fixierung), liegen die Wendestellen bei der Polynomeninterpolation nahe an den Stützstellen, bei der polynomialen Bestapproximation sogar in den Stützstellen.
Die Begriffe Splineinterpolation bzw. Splinefunktion ohne weitere Zusätze bezeichnen immer die Splineinterpolation bzw. Splinefunktion dritten Grades. Beide Begriffe werden zumeist synonym verwendet. Der Begriff Spline wird jedoch zunehmend als Abkürzung für B-Spline, seltener auch für andere splineartige Linien wie die Bézierkurven, benutzt.
Smoothing Splines sind Splines, die nicht durch jeden Datenpunkt verlaufen müssen und können zur Signalglättung benutzt werden.
Gegebenheiten
Gegeben: eine natürliche Zahl
und
Stützstellen
sowie
Funktionswerte
.
Gesucht ist eine stückweise polynomiale Funktion, ein Spline,
mit
für
,
bei der für
die Einschränkungen
auf die Teilintervalle
Polynome sind.
Linear (einfacher Streckenzug)
Die einfachste Methode ist die Verwendung von Geraden zwischen jeweils zwei benachbarten Punkten, die Berechnung eines einfachen Splines als Streckenzug erfolgt auf dieselbe Weise, mit der man auch den Graphen zwischen zwei Punkten ermittelt:
oder auch
Diese „einfachen“ Spline-Polynome können – wie oben angesprochen – sehr ungenau sein. Wesentlich bessere Ergebnisse liefern kubische Spline-Polynome.
Kubisch (Polynome 3. Grades)
Bei der Verbindung von Punkten mit Polynomen höheren Grades müssen zusätzlich zu den Stützstellen Eigenschaften definiert werden, wie die Polynome ineinander übergehen. Für kubische Splines sind in einer Dimension 4 Koeffizienten zu bestimmen und zwei weitere Bedingungen sind zu definieren.
Der kubische C²-Spline
C2
fordert, dass die zusammengesetzte Funktion
aus allen Einschränkungen (Teilintervallen)
zweimal stetig differenzierbar ist. Dafür wird gefordert, dass die erste und
zweite Ableitung der Einschränkungen an den Stützstellen
und
für
übereinstimmen.
Prinzipiell gilt, dass sich eine Änderung einer Stützstelle
stets global auf den gesamten Spline
auswirkt, jedoch wird der Einfluss der Änderung mit zunehmender Distanz zu
– anders als bei Interpolationspolynomen
– stark gedämpft. Kubische Splines neigen daher weniger zum Überschwingen.
Der kubische C2-Spline erfüllt eine Minimalitätseigenschaft der zweiten Ableitung, was ihn gegenüber anderen Interpolationen besonders interessant macht.
Konstruktion
Es ist ersichtlich, dass die zweite Ableitung von
ein linearer Spline ist. Diese kann daher wie oben
beschrieben durch folgende Form beschrieben werden:
mit
für .
sind die sogenannten Momente,
welche den Werten von
an den Stützstellen entsprechen und im Folgenden zu berechnen sind. Durch
zweifache Integration und geschickte Umformung entstehen aus diesen Gleichungen
Polynome dritten Grades mit zwei weiteren Parametern
und
der Form:
.
Um die Stetigkeitsbedingungen
und
zu erfüllen, wählen wir
und
.
Mit diesem Ansatz stimmen bereits die nullten und die zweiten Ableitungen der
Einschränkungen
an den Stützstellen überein. Die Momente sind so zu wählen, dass auch die ersten
Ableitungen an den Stützstellen gleich sind. Mit
und
lassen sich folgende Gleichungen aufstellen:
für
.
Für
und
fehlen hier zwei Gleichungen, welche sich aus den Randbedingungen
ergeben.
Dieses lineare Gleichungssystem kann auch durch folgende, tridiagonale, streng diagonaldominante Matrix ausgedrückt werden:
Die Werte für die
hängen von den Randbedingungen ab.
Zur Lösung kann hier auf den komplizierten Gauss-Algorithmus verzichtet werden und z.B. ein einfacher Vorwärts-Durchlauf zur Elimination der Elemente unter der Hauptdiagonalen mit anschließender Rückwärtssubstitution verwendet werden (Thomas-Algorithmus).
Randbedingungen
Prinzipiell gibt es ein Interpolationsintervall weniger als Stützstellen (Zaunpfahlproblem). Das heißt, dass zwei Gleichungen zur Bestimmung aller Koeffizienten fehlen. Diese ergeben sich aus den Randbedingungen. Typische Randbedingungen sind:
- Natürliche Randbedingungen (auch freier Rand)
- Bedingung:
,
- Bedeutung: Das Spline schließt mit Wendepunkten ab.
- Berechnung:
und
- Hermite Randbedingungen (auch eingespannter Rand)
- Bedingung:
,
- Bedeutung:
und
sind vorgegeben, normalerweise entweder durch die Ableitung einer zu interpolierenden Funktion
oder durch eine Approximation derselben.
- Berechnung:
- periodische Randbedingungen
- Bedingung: Intervall
,
,
,
- Bedeutung: Nullte, erste und zweite Ableitung von
am Anfang und am Ende des Intervalls sind gleich.
- Berechnung: Es wird eine zusätzliche Stützstelle
eingeführt, welche das Intervall begrenzt. Die Anzahl der Gleichungen zur Berechnung der Momente und die Größe der Matrix bleibt jedoch gleich, da
bereits gegeben ist, damit die zweiten Ableitungen übereinstimmen. Für die erste- und letzte Zeile der Matrix gilt:
- Außerdem sind die Ecken der Matrix abseits der Hauptdiagonalen hier nicht
Null:
- Die Lösung dieses Systems ist daher komplizierter. Im Falle äquidistanter Stützstellen lässt sich für diesen Fall eine Transformation anwenden.
- not-a-knot Randbedingungen
- Bedingung:
,
- Bedeutung: Die äußeren drei Punkte werden je durch ein gemeinsames Polynom interpoliert, was zum Beispiel durch Gleichsetzen der dritten Ableitungen erfolgen kann. Für Splines bis einschließlich vier Stützstellen geht der not-a-knot Spline daher in ein gewöhnliches Interpolationspolynom über. Verwendet wird der not-a-knot-Spline zum Beispiel vom Programm Matlab.
- Berechnung: Es gelte
. Für die Vorwärtssubstitution wird zunächst die Randbedingung an
betrachtet. Hierfür können folgende Werte verwendet werden:
- Falls
entsteht hier eine Division durch Null und es muss eine Grenzwertbildung bis in die dritte Zeile der Matrix (Null ist hier der Index der ersten Zeile/Spalte) erfolgen:
- Gelöst wird nun lediglich die Untermatrix beginnend bei
und das Randpolynom
auf dem Intervall
wird durch eine zusätzliche Polynominterpolation bestimmt, sodass
,
,
,
.
ist dadurch bereits erfüllt.
- Nach dem Vorwärtsdurchlauf zur Elimination der Elemente unter der
Diagonalen wird nun die Randbedingung an
betrachtet:
Weitere Randbedingungen sind gebräuchlich, wie etwa integrale Randbedingungen oder die im Folgenden vorgestellte, symmetrische Verlängerung.
Optimierung des Rechenaufwands
Bei äquidistanten Stützstellen mit konstantem Abstand
vereinfacht sich das Gleichungssystem zu
für
.
Mit der symmetrischen Verlängerung
und
entsteht daraus eine sogenannte Tridiagonal-Toeplitz-Matrix,
welche besonders effizient, auch parallel gelöst werden kann. Für die rechte
Seite kann hier
und
angesetzt werden. Mit
lässt sich schreiben:
Diese hat die Inverse
mit Koeffizienten ,
die den Gleichungen
,
,
der Rekursion
und explizit der Formel
genügen.
Minimalitätseigenschaft der zweiten Ableitung
Unter allen zweimal stetig differenzierbaren Funktionen, die alle
Stützstellen innerhalb eines Intervalls
miteinander verbinden, hat unter Verwendung natürlicher, periodischer oder
Hermite-Randbedingungen der kubische Spline die geringste Krümmung:
,
wobei
hier eine beliebige Funktion auf
aus C2 ist, die alle Stützstellen schneidet. Anschaulich folgt
daraus, dass ein zu volles Glas Wasser, das während einer Zugfahrt auf dem Tisch
steht, „am wenigsten überschwappt“, wenn der Streckenzug der Schienenführung
mithilfe kubischer Splines parametrisiert wurde.
Diese sogenannte Identität von Holladay wurde im Jahr 1957 von
Holladay
bewiesen. Sei mit
der Raum der zweimal differenzierbaren Funktionen bezeichnet, für welche die
nullte und erste Ableitung absolutstetig
sind und die zweite Ableitung in
liegt. Sei nun
eine interpolierende Splinefunktion zu einer beliebigen Funktion
und
die
-Norm,
so gilt:
mit
.
Erfüllt die Splinefunktion die natürlichen, periodischen oder vollständigen
Randbedingungen, so ist ,
also:
Damit gilt nun:
Bikubischer C2-Spline
Der bikubische C2-Spline ist die Verallgemeinerung des einfachen, kubischen C2-Splines auf zwei Dimensionen, man spricht hierbei auch von multivariater Interpolation. Dafür müssen die zu interpolierenden Punkte zij in einem rechteckigen Gitter angeordnet sein. Jede zwischen vier Punkten aufgespannte Fläche Aij wird durch ein zweidimensionales Polynom von 16 Koeffizienten charakterisiert:
Für einen zweidimensionalen C2-Spline müssen die Koeffizienten so
gewählt werden, dass die aus allen Flächen zusammengesetzte Funktion
zweimal stetig in x- und y-Richtung differenzierbar ist. Das heißt, neben S
selbst sind die folgenden Ableitungen stetig auf ganz
:
Konstruktion
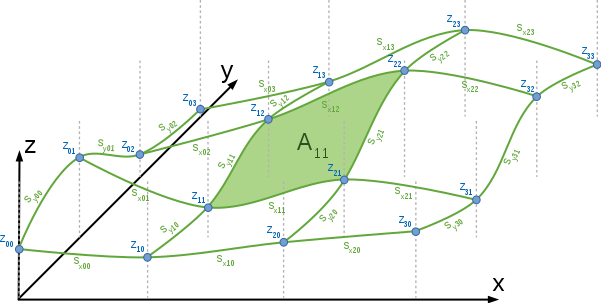
Es ist ersichtlich, dass jeder Schnitt durch eine Teilfläche
parallel zur
-
oder
-Achse
eine eindimensionale Kurve liefert, welche durch ein kubisches Polynom von vier
Koeffizienten beschrieben werden kann. Daraus folgt, dass die vier Ränder jeder
Teilfläche solche Polynome sind. Um die geforderte zweifach stetige
Differenzierbarkeit zu erhalten, können zunächst alle Punkte entlang der
Gitterlinien eindimensional interpoliert werden. Das bikubische Spline erbt
dabei die verwendeten Randbedingungen der eindimensionalen Splines.
Nun stehen zu jedem zweidimensionalen Polynom
mit 16 Koeffizienten vier eindimensionale Randpolynome
,
,
,
mit je 4 Koeffizienten zur Verfügung. Hierbei kennzeichnet der erste Index der
s, zu welcher Achse sie parallel verlaufen.
Um diese Randpolynome zu
„zusammenzurechnen“ ist ein System von 16 linearen Gleichungen aufzustellen.
Vier Gleichungen ergeben sich aus der Forderung, dass S an den Gitterpunkten
genau die Werte
annimmt:
Weitere vier Gleichungen ergeben sich aus der Ableitung der zur -Achse
parallelen Randpolynome nach
:
Weitere vier Gleichungen aus der Ableitung der zur -Achse
parallelen Randpolynome nach
:
Nun ergibt sich das Problem, dass entlang jedem der vier Ränder zwei Punkte
und zwei Ableitungen gegeben sind. Damit ist ein Polynom von Grad 3 entlang des
jeweiligen Randes eigentlich vollständig spezifiziert. Das hinzunehmen
z.B. der zweiten Ableitungen an den Eckpunkten oder weiterer
Funktionswerte entlang der Randpolynome würde eine lineare Abhängigkeit im
Gleichungssystem erzeugen. Mit den gegebenen Gleichungen lassen sich jedoch nur
12 der 16 Koeffizienten bestimmen. Ein nicht linear abhängiges System ergibt
sich durch Hinzunahme der gemischten Ableitungen nach x und y. Setzt man diese
in den Eckpunkten etwa auf null, so ist
nur in den Eckpunkten zweimal stetig differenzierbar. Entlang der Ränder ergeben
sich in den zweiten Ableitungen jedoch Sprünge. Aus den Randpolynomen lassen
sich die gemischten Ableitungen jedoch nicht direkt berechnen.
Um nun korrekte Werte für diese gemischten Ableitungen zu erhalten, welche
auch entlang der Ränder stetige, zweite Ableitungen von
liefern, kann wie folgt vorgegangen werden:
- Entlang der Gitterlinien, welche parallel zur
-Achse verlaufen, werden weitere, eindimensionale Splines
gebildet
- Diese interpolieren statt der
-Werte die Ableitungen von
an deren Schnittpunkten mit den
-Gitterlinien
- Die
-Splines können nun nach
abgeleitet werden. Daraus ergeben sich die gemischten Ableitungen
Wie beim eindimensionalen C2-Spline wirkt sich auch beim
bikubischen Spline eine Änderung in einer Stützstelle (Datenpunkt) generell auf
alle Teilflächen aus. Dies veranschaulicht, warum eine Konstruktion alleine aus
den Randpolynomen
und
fehlschlägt: Diese ändern sich nur, wenn ein Datenwert, welcher parallel (in
-
oder
-Richtung)
zur betrachteten Teilfläche liegt, geändert wird. In der Abbildung
rechts hat eine Änderung von
keinen Einfluss auf die 1D-Splines, welche den Rand von
bilden. Erst die erneute Interpolation durch
erzeugt eine Abhängigkeit zwischen diesem Punkt und der Fläche.
Beispiel
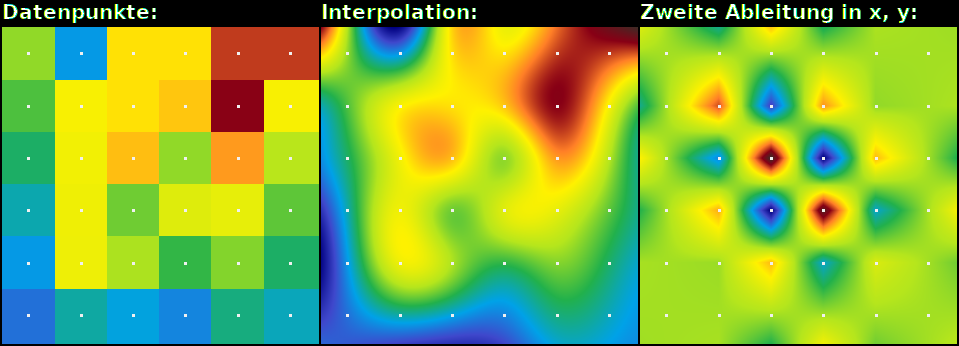
Beispiel für bikubische Interpolation:
Ein Datenblock aus 6x6 Werten (links) wird bikubisch interpoliert (mitte). Dabei
wurden natürliche Randbedingungen angenommen (die zweite Ableitung auf den
Randpunkten ist null). Die Farben zwischen linkem und mittlerem Bild wurden
synchronisiert und beschreiben die Funktionswerte ähnlich der Farben auf einer
Landkarte zur Illustration der Höhe. Um die Korrektheit der Interpolation zu
verdeutlichen, wird rechts die zweite Ableitung
gezeigt. Diese besteht aus linearen Funktionen und ist immer noch stetig.
Interpolation mit Formerhaltung
Splines sind aufgrund ihrer Eigenschaften im CAD
weit verbreitet. Es stellt sich die Frage, unter welchen Bedingungen eine
Spline-Interpolante eine der folgenden formerhaltenden Eigenschaften der zu
interpolierenden Funktion
erbt:
- Nichtnegativität:
für alle
- Monotonie:
für
- Konvexität:
für alle
und
Hier zeigt sich, dass klassische Splines etwas schlechtere Eigenschaften haben als Bézierkurven. Zunächst stellt sich die Frage, wann ein interpolierender Spline konvex ist.
Für klassische Splines gilt, dass die Menge möglicher Splines auf dem
Intervall
zum Gitter
ein endlichdimensionaler Vektorraum
ist. Für die Interpolation werden (nicht notwendig mit dem Gitter
zusammenfallenden) Knoten
und zugehörige Ordinaten
vorgegeben und gefordert, dass der Spline
stetig differenzierbar in
ist und darüber hinaus
für
gilt. Fordert man zusätzlich die Konvexität des interpolierenden Splines und
geringe technische Annahmen, so stellt man fest, dass die Menge
aller Ordinatentupel
,
für die ein solcher Spline existiert, abgeschlossen
ist.
Das hat weitreichende Konsequenzen.
ist eine echte Teilmenge des
,
falls
,
da die Eingangsdaten nicht in konvexer Lage zu sein brauchen. Bei Vorgabe eines
Tupels auf dem Rand von
kann infolge Rechenungenauigkeiten oder anderer Störungen die Menge
verlassen worden sein, so dass trotz Lösbarkeit des Ausgangsproblems keine
Lösung gefunden wird. Die andere Folgerung des Satzes ist noch schlimmer. Dazu
seien fünf Punkte in Form des Zeichens „
“
so angeordnet, dass der mittlere Punkt genau auf der Spitze liegt. Die einzige
konvexe Interpolierende ist dann die Betragsfunktion,
und diese ist nicht stetig differenzierbar. Also gehört das 5-Tupel zum
Komplement von
,
und dieses ist offen.
Somit gibt es eine Umgebung
des 5-Tupels, in der es ebenfalls keine konvexe, stetig differenzierbare
Interpolierende gibt. Verschiebt man den mittleren Punkt geringfügig nach oben,
ohne die Umgebung zu verlassen, dann erhält man folglich fünf Punkte in streng
konvexer Lage, zu denen dennoch die Interpolationsaufgabe keine Lösung besitzt.
Da dieser Effekt bei Vorgabe vieler Interpolationspunkte zunimmt, bleibt nur ein
Ausweg, die Lösbarkeit für Eingangsdaten in streng konvexer Lage zu
gewährleisten, nämlich die Voraussetzungen des Satzes zu verletzen. Die Menge,
aus der die Splines entnommen werden dürfen, soll kein endlichdimensionaler
Vektorraum sein. Dafür bieten sich u. a. an:
- (gebrochen-)rationale Splines
- Splines mit frei wählbaren Zwischenknoten
- Exponentialsplines
- lakunäre (lückenhafte) Splines
Literatur
- Stoer, Bulirsch: Numerische Mathematik 1. 10. Auflage. Springer Verlag, Berlin, Heidelberg, New York 2007, ISBN 978-3-540-45389-5, 2.5 Spline-Interpolation, S. 112–148 (mit Beispielen, Beweisen, Übungsaufgaben und umfangreichen Angaben zu weiterer speziellerer Literatur).


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.11. 2021