
Oszillation (Topologie)
In der Mathematik kommt der Begriff der Oszillation in der Topologie vor, einem der Teilgebiete der Mathematik. Er tritt ebenfalls in der Analysis und hier insbesondere in Integralrechnung auf. Statt von der Oszillation spricht man auch von der Schwankung oder der Schwankungsbreite. Die Oszillation dient bei der Untersuchung von Stetigkeitsfragen zu Abbildungen von topologischen Räumen in metrische Räume dazu, in einem gewissen Sinne die Unstetigkeit einer Abbildung zu messen. Mit dem Begriff der Oszillation verwandt ist der des Stetigkeitsmoduls von Abbildungen metrischer Räume.
Oszillation einer Folge
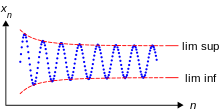
Sei
eine Folge reeller Zahlen. Die Oszillation
ist definiert als Differenz zwischen dem Limes
superior und Limes inferior von
:
.
Die Oszillation einer Folge ist genau dann null, wenn die Folge konvergiert.
Die Oszillation ist nicht definiert, wenn Limes Superior und Limes Inferior
beide gleichzeitig gleich
oder gleich
sind, wenn also die Folge bestimmt
divergiert.
Definitionen, Sprech- und Schreibweisen
Gegeben sei ein topologischer Raum ,
ein metrischer Raum
sowie eine Abbildung
.
Oszillation auf einer Teilmenge
Für eine beliebige nicht-leere
Teilmenge
versteht man unter der Oszillation von
auf
bzw. unter der Schwankung von
auf
den Durchmesser
der Bildmenge
bezüglich der Metrik
,
also diejenige Größe
,
welche folgendermaßen definiert ist:
Es wird im Allgemeinen auch die Oszillation
nicht ausgeschlossen, wenn – wie im Falle unbeschränkter
Funktionen möglich – kein
endliches Supremum
existiert.
Ein häufig betrachteter Fall ist der, dass
ist, wobei
die Betragsmetrik, also die durch die Betragsfunktion
gegebene darstellt, während zugleich
auf
beschränkt
ist. Unter diesen Gegebenheiten ist
Hinsichtlich der Bezeichnung findet man statt
auch
oder
;
manchmal auch, jedoch eher in englischsprachigen Quellen,
.
Oszillation in einem Punkt

Für einen Punkt
definiert man:
Man nennt diese Größe die Oszillation von
im Punkte
oder die Oszillation von
in (bei)
oder auch die Punktschwankung von
in (bei)
.
Das obige Infimum
wird dabei definitionsgemäß über alle
-Umgebungen
im Umgebungsfilters
gebildet. Es genügt jedoch für dessen Bestimmung auch schon, allein die offenen
Umgebungen innerhalb
oder gar nur die
-Umgebungen
einer beliebigen in
enthaltenen Umgebungsbasis
zu betrachten.
Statt
gibt es auch die Schreibung
bzw.
. Daneben ist, sofern aus dem Kontext heraus die Abhängigkeit von
keiner Hervorhebung bedarf, die einfache Schreibung
bzw.
zu finden.
Wird die topologische
Struktur von
ebenfalls durch eine Metrik
erzeugt, so hat der Umgebungsfilter des Punktes
die
-Umgebungen
(
)
als Umgebungsbasis
und es gilt:
Untersuchungen zur Oszillation treten oft – etwa in der Integralrechnung –
für den Fall auf, dass die betrachteten Funktionen auf reellen Intervallen
leben, also
ist und zugleich
eine beschränkte
Funktion ist.
Da für einen Punkt
die offenen
Intervalle der Form
und auch die abgeschlossenen
Intervalle der Form
eine Umgebungsbasis bilden, hat man:
.
Beispiel
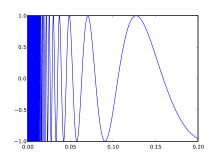
Für die Funktion
ist
für
und
.
Resultate
- Die Funktion
ist eine oberhalb stetige Funktion.
- Für eine Abbildung von einem topologischen in einen metrischen Raum ist
Stetigkeit in einem Punkte gleichbedeutend damit, dass in diesem Punkt die
Oszillation gleich Null ist. Mit anderen Worten heißt das für
ist
in
stetig genau dann, wenn
ist. Eine Abbildung von einem topologischen in einen metrischen Raum ist folglich stetig genau dann, wenn sie in keinem Punkte eine Oszillation größer Null aufweist.
- Bezeichnet man mit
die Menge der Unstetigkeitsstellen von
und setzt man
mit
, so gilt
.
- Die
sind allesamt abgeschlossene Mengen und damit ist
stets eine Fσ-Menge.
- Ist
ein abgeschlossenes n-dimensionales Intervall und
eine beschränkte reelle Funktion, so ist
dann und nur dann Riemann-Darboux-integrierbar, wenn die
allesamt Jordan-Nullmengen sind.
Zum Stetigkeitsmodul
Der mit der Oszillation verwandte Begriff des Stetigkeitsmoduls wurde von Henri
Léon Lebesgue im Jahre 1910 eingeführt. Das Stetigkeitsmodul zu einer
Abbildung
zwischen zwei metrischen Räume
und
und einer gegebenen reellen Zahl
ist dabei die folgende Größe
:
Der Stetigkeitsmodul hat folgende Eigenschaften:
.
ist monoton steigend.
ist subadditiv.
ist gleichbedeutend damit, dass
gleichmäßig stetig ist.
Siehe auch
Literatur
- Hermann Athen, Jörn Bruhn (Hrsg.): Lexikon der Schulmathematik und angrenzender Gebiete. Band 4: S–Z. Aulis Verlag, Köln 1978, ISBN 3-7614-0242-2.
- Nicolas Bourbaki: Elements of Mathematics. General Topology. Part 2 (= ADIWES International Series in Mathematics). Addison-Wesley Publishing Company, Reading MA 1966.
- Harro Heuser: Lehrbuch der Analysis. Teil 1 (= Mathematische Leitfäden). 16., durchgesehene Auflage. B. G. Teubner Verlag, Stuttgart 2006, ISBN 978-3-8351-0131-9.
- Serge Lang: Analysis. Hrsg.: Willi Jäger. Inter European Editions, Amsterdam 1977, ISBN 0-201-04152-9 (Deutsche Übersetzung von Bernd Wollring).
Anmerkungen
- ↑
Stellenweise wird sogar eine noch allgemeinere
Situation zugrundegelegt. Dann betrachtet man in
eine nicht-leere Teilmenge
sowie eine Abbildung
und definiert dann
. Aus Vereinfachungsgründen wird dann bei
gesetzt. Vgl. hierzu S. Willard: General Topology. 1970, S. 177.
- ↑
Bei N. Bourbaki: Elements
of Mathematics. 1966, S. 151. wird diese Größe auch
allgemeiner für
,
und
definiert.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.11. 2021