Biegelinie
Eine Biegelinie (auch Biegungslinie, Durchbiegungslinie, elastische Linie) ist eine mathematisch einfach beschreibbare Kurve für die Verformung eines geraden Balkens bei mechanischer Belastung.
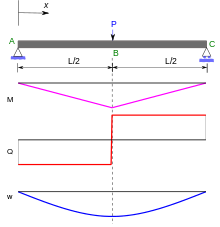
Die Gleichung der Biegelinie ist ein Teil der Balkentheorie. Sie wird verwendet, um die Durchbiegung von Balken im Bereich des linear-elastischen Materialverhaltens zu bestimmen. Dabei wird die Annahme zugrunde gelegt, dass die eintretenden Verformungen so klein sind, dass die biegebedingte Veränderung der Balkengeometrie bei der Aufstellung der Gleichung vernachlässigt werden kann. Für den Bereich des nichtlinear-elastischen Materialverhaltens sind Abänderungen erforderlich.
Das Biegemoment
(Schnittmoment) an der Stelle
in einem elastischen geraden Balken bestimmt die dortige Krümmung
seiner Biegelinie
.
Unter Einbeziehung des Hooke’schen Stoffgesetzes erhält man
.
Dabei bezeichnen ,
und
den (vorzeichenbehafteten) Krümmungsradius an der Stelle
,
den Elastizitätsmodul bzw. das axiale
Flächenträgheitsmoment des Balkens. Das Minuszeichen berücksichtigt die für
Schnittreaktionen
üblichen Richtungskonventionen.
Mit der rein geometrischen Definition einer Kurvenkrümmung folgt daraus die exakte Differentialgleichung der Balkenbiegung zu
.
Die Striche bezeichnen die Ableitung nach der Balkenlängskoordinate .
In den meisten praktischen Fällen ist die Durchbiegung
so klein, dass
bleibt. Dann genügt die einfachere Differentialgleichung
zur Bestimmung der Biegelinie .
Differenzialbeziehungen
In der schubweichen Balkentheorie II. Ordnung gibt es unter den Bernoullischen Annahmen folgende Differentialgleichungen für die Queranteile:
mit
- der Laufkoordinate x entlang der Balkenachse
- dem Elastizitätsmodul E
- dem Schubmodul G (Term tritt in der schubstarren Theorie nicht in den Differentialgleichungen auf)
- dem Flächenträgheitsmoment I(x)
- R(x) der Transversalkraft (in der Theorie I. Ordnung gilt R(x)=V(x))
- V(x) der Querkraft
- NII(x) die Normalkraft nach Theorie Theorie II. Ordnung (in derTheorie I. Ordnung tritt dieser Term in der Differenzialgleichung nicht auf)
- q(x) der Gleichlast (Querbelastung pro Längeneinheit)
- M(x) dem Biegemoment
- m(x) dem Steckemoment (Biegebelastung pro Längeneinheit)
- φ(x) der Verdrehung
- κe(x) der eingeprägten Krümmung
- w(x) der Durchbiegung zufolge Belastung
- wv(x) der Durchbiegung zufolge Vorverformung
der Schubfläche (Term tritt in der schubstarren Theorie nicht auf).
Durch diese Differentialgleichungen ist somit ein Zusammenhang zwischen der
Durchbiegung
und dem Biegemoment
im Balken gegeben. Dies führt zu drei Gleichungen, für die ein Zusammenhang
zwischen der Durchbiegung
und den Schnittlasten
im Balken (Biegemoment
und Querkraft
)
sowie der äußeren Flächenlast
gegeben ist. (Die Koordinate
wird hierbei entlang der Balkenachse gezählt. Die Biegung erfolgt um die
Koordinaten-Achse
.
Die Koordinate
verläuft in Richtung der Querkraft.)
Die letzte Gleichung vierter Ordnung heißt auch Euler-Bernoulli-Gleichung.
Damit die Durchbiegung berechnet werden kann, muss der Elastizitätsmodul
des Materials bekannt sein. Ferner muss vorab das Flächenträgheitsmoment
des Balkenquerschnitts ermittelt und der Verlauf der äußeren Streckenlast
oder der Verlauf von Biegemoment
oder Querkraft
bestimmt werden. Die Gleichung kann dann mehrmals integriert werden, bis auf der
einen Seite die Durchbiegung
steht. Hierbei ergeben sich mehrere Integrationskonstanten, die durch eine
entsprechende Anzahl von Randbedingungen
bestimmbar sind.
Das folgende Beispiel zeigt das Vorgehen, wenn vorab der Verlauf des
Biegemoments
ermittelt wurde und der Elastizitätsmodul und das Flächenträgheitsmoment über
die ganze Länge des Balkens als konstant angenommen werden:
Es ergeben sich die zwei unbekannten Konstanten
und
.
Diese können nun durch zwei Randbedingungen bestimmt werden. Zum Beispiel gilt
bei einem Auflager an der Stelle
,
welches eine Querkraft aufnehmen kann:
.
Für ein Auflager an der Stelle
,
welches ein Moment aufnehmen kann, gilt:
.
Kreismembran
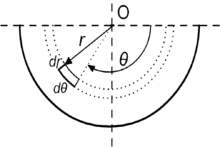
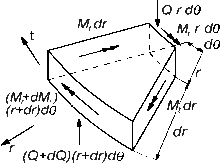
Im Falle einer kreisrunden Membran werden oft auch vereinfacht die Formeln aus der Balkentheorie verwendet. Unter der Annahme einer homogenen Membran wird dann bei rotationssymmetrischen Kräften eine einfache Biegelinie berechnet. Also nur ein Querschnitt der Membran.
Mit dem tangentialen und radialen Biegemoment
und
und unter Vernachlässigung von Differentialen höherer Ordnung ergibt sich die
Momentgleichung
Die Biegemomente lassen sich über die Poissonzahl
angeben zu:
D ist hierbei das Widerstandsmoment,
das sich über den Elastizitätsmodul
der Membran mit Dicke d wie folgt beschreiben lässt:
Die Biegelinie einer Kreismembran lautet dann in Differentialform, unter Vernachlässigung von kleinen Termen höherer Ordnung sowie von Zugspannungen (nur zulässig für geringe Dehnungen):


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 25.07. 2020