Flächenträgheitsmoment
| Physikalische Größe | |||||||
|---|---|---|---|---|---|---|---|
| Name | Flächenträgheitsmoment | ||||||
| Formelzeichen | |||||||
| |||||||
Das Flächenträgheitsmoment, auch als Flächenmoment 2. Grades bezeichnet, ist eine in der Festigkeitslehre verwendete, aus dem Querschnitt eines Trägers abgeleitete geometrische Größe, die zu dessen Verformungs- und Spannungsberechnung bei Biege- und Torsionsbeanspruchung eingeführt wurde. Die verwendeten Formeln enthalten das Flächenträgheitsmoment neben anderen Größen, wie solchen für die Belastung und für die Eigenschaften des verwendeten Werkstoffs.
Mit Hilfe des Flächenträgheitsmomentes werden auch diejenigen Belastungen berechnet, deren Überschreiten zum Knicken von Stäben oder Beulen von Schalen führt.
Das Flächenträgheitsmoment darf nicht mit dem (Massen-)Trägheitsmoment verwechselt werden, das die Trägheit eines rotierenden Körpers gegenüber einer Winkelbeschleunigung charakterisiert.
Arten
Axiales Flächenträgheitsmoment
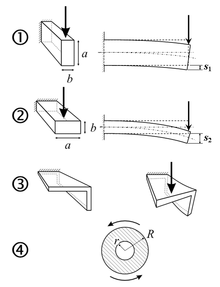
Mit dem axialen Flächenträgheitsmoment Ia wird die Querschnitts-Abhängigkeit der Verbiegung eines Balkens unter Belastung zusammenfassend beschrieben. Die Verbiegung und die im Querschnitt entstehenden inneren Spannungen sind umso kleiner, je größer das axiale Flächenträgheitsmoment ist. Das wesentlichste Maß im Querschnitt ist dabei die Ausdehnung in Richtung der angreifenden Kraft. Im nebenstehenden Bild ist dargestellt, dass eine vertikale Last einen Balken weniger verbiegt, wenn er hochkant anstatt flach angeordnet ist (Vergleich zwischen den Teilbildern 1 und 2).
Polares Flächenträgheitsmoment
Mit dem polaren Flächenträgheitsmoment Ip wird das
Flächenträgheitsmoment einer Fläche um einen zu definierenden Punkt (meist ihr
Schwerpunkt) beschrieben. Das wesentlichste Maß im Querschnitt ist dabei die
radiale Ausdehnung (R im Teilbild 4 der nebenstehenden Abbildung). Nur bei
kreisförmigen Flächen stimmt das polare Flächenträgheitsmoment mit dem Torsionsträgheitsmoment
überein. Für andere Geometrien der Fläche lässt sich das Torsionsträgheitsmoment
meist nur numerisch berechnen.
Biaxiales Flächenträgheitsmoment
Das biaxiale Flächenträgheitsmoment, auch als Flächendeviationsmoment oder Flächenzentrifugalmoment bezeichnet, wird benutzt zur Berechnung der Verformung und der Spannungen
- bei belasteten asymmetrischen Profilen (Teilbild 3 in nebenstehender Abbildung)
- bei asymmetrischer Belastung symmetrischer (oder beliebiger) Profile.
Das Flächendeviationsmoment bzw. Flächenzentrifugalmoment (Einheit m4) darf nicht mit dem (Massen-)Deviationsmoment bzw. (Massen-)Zentrifugalmoment verwechselt werden (Einheit kg·m2).
Berechnung
Einheiten
Die Flächenträgheitsmomente werden üblicherweise in cm4, mm4 oder auch m4 angegeben (SI-Einheiten). Im veralteten, in den USA aber noch gebräuchlichen Einheitensystem werden sie normalerweise in in4 notiert.
Axiales Flächenträgheitsmoment
Die axialen Flächenträgheitsmomente lassen sich durch diese Gleichungen beschreiben:
- z = senkrechter Abstand der y-Achse zum Element dA
- y = senkrechter Abstand der z-Achse zum Element dA
Beide Größen können nur positive Werte annehmen.
Polares Flächenträgheitsmoment
Das polare Flächenträgheitsmoment setzt sich aus den beiden
Flächenträgheitsmomenten
und
zusammen:
Biaxiales Flächenträgheitsmoment
Das biaxiale Flächenträgheitsmoment wird durch diese Gleichung beschrieben:
Diese auch Deviations- oder Zentrifugalmoment genannte Größe ist gleich Null, wenn die y-Achse oder die z-Achse eine Symmetrieachse des Querschnitts ist. Die zugehörigen Flächenträgheitsmomente heißen dann Hauptträgheitsmomente, sie nehmen in diesem Falle extremale Werte an. Im Gegensatz zu den axialen und zum polaren Flächenträgheitsmoment kann diese Größe sowohl positive als auch negative Werte annehmen. Neben dieser Definition mit negativem Vorzeichen wird je nach Literatur auch eine Definition mit positivem Vorzeichen verwendet, dies ist in allen Formeln, die das Deviationsmoment verwenden, zu berücksichtigen.
Satz von Steiner
Alle hier genannten Flächenträgheitsmomente werden auf einen speziellen Punkt, nämlich den Flächenschwerpunkt (Flächenmittelpunkt), bezogen. Für alle anderen Punkte können die Flächenträgheitsmomente mit dem Steinerschen Satz berechnet werden.
Der 1840 von Jakob
Steiner aufgestellte Satz
besagt, dass sich das Flächenträgheitsmoment einer beliebigen Querschnittsfläche
zusammensetzt aus den Flächenträgheitsmomenten in den Flächenmittelpunkten der
einzelnen Teilflächen und dem Produkt aus dem Quadrat des Abstandes z von
Schwerachse-Gesamtfläche zu Schwerachse-Teilfläche und Teilfläche A. Ein
Anwendungsbeispiel ist die I-Form. Die Flächenträgheitsmomente der drei
rechteckigen Teilflächen, nämlich der beiden horizontalen Flansche und des
vertikalen Stegs, lassen sich über die unten angegebenen Formeln bestimmen und
für die vertikale z-Achse zu
einfach summieren, denn alle Schwerpunkte der Teilflächen liegen auf der
gemeinsamen Schwerachse z der Gesamtfläche. Das Flächenträgheitsmoment
bezüglich der y-Achse setzt sich ebenfalls aus den drei Summanden plus dem
Steiner'schen Anteil der beiden Flansche zusammen.
Die Formeln sind nur gültig, wenn auf der rechten Seite der Gleichung die Flächenträgheitsmomente stehen, die sich auf ein Koordinatensystem im Flächenmittelpunkt beziehen, während die Flächenträgheitsmomente auf der linken Seite für ein beliebiges (dazu parallel liegendes) Koordinatensystem gelten.
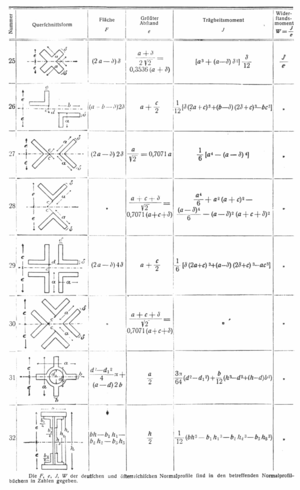
Flächenträgheitsmoment für beliebige Polygone
Trägheitsmomente beliebiger geschlossener Polygone können mit folgenden
Formeln berechnet werden, wenn die Punkte gegen den Uhrzeigersinn eingegeben
werden. Die Trägheitsmomente beziehen sich auf den Koordinatenursprung. Das
Vorzeichen des Deviationsmoments
ist konform zu den Formeln zur Koordinatentransformation. Das Polygon hat n-1
Punkte und beginnt mit Punkt 1 und endet mit Punkt n, welcher identisch Punkt 1
ist. Der Punkt i hat also die Koordinaten
.
Die Formeln wurden durch Anwendung der Gaußschen Trapezformel hergeleitet[5].
Hauptträgheitsmomente und verdrehte Trägheitsmomente
,
,
,
Winkel zur Hauptträgheitsachse:
Mit Hilfe dieser Formeln kann man die zugehörigen Trägheitsmomente einer
Fläche berechnen, wenn die Koordinatenachsen
der Fläche um einen beliebigen Winkel
verdreht werden. Bei Drehung um den Winkel
werden
und
extremal und
.
Bezugsachsen, die durch den Winkel
beschrieben werden, nennt man Hauptträgheitsachsen.
Da in früheren Jahren noch keine zuverlässigen Rechenmaschinen
zur Verfügung standen, wurde ein grafisches Verfahren von Christian Otto Mohr
angegeben. Der Mohrsche
Trägheitskreis ist noch in vielen Lehrbüchern über die Technische Mechanik
zu finden. Eine praktische Anwendung finden die verdrehten
Flächenträgheitsmomente bei der Berechnung von Spannungen, wenn
bei der Biegung
das belastende Biegemoment
nicht in die Richtung eines der beiden Hauptträgheitsmomente fällt.
Abgeleitete Größen
Widerstandsmoment
Das Widerstandsmoment
kann man in der linearen Elastizitätstheorie verwenden, um die am
Querschnitts-Rand auftretende größte Beanspruchung (Spannung) zu
bestimmen. Es ist der Quotient aus dem Flächenträgheitsmoment und dem Abstand
des Randes von der neutralen
Faser:
Flächenträgheitsradius
Für geometrisch ähnliche Bauteile (z.B. Rechtecke mit gleichem Breiten/Höhen-Verhältnis) lässt sich auch der Flächenträgheitsradius mit der Dimension Länge definieren, mit dem man Körper vergleichen kann, die im Sinne des Flächenmomentes 2. Grades ähnlich sind:
Der Flächenträgheitsradius wird oft „Trägheitsradius“
genannt, was aber Verwechslungsgefahr zum Streumassenradius
birgt. Außerdem ist der Flächenträgheitsradius im Schlankheitsgrad
enthalten.
Flächensteife / Flächensteifigkeit
Die selten verwendete Flächensteife (kein Formelzeichen), auch Flächensteifigkeit genannt, ist das Quadrat des Trägheitsradius bzw. der Quotient aus Flächenträgheitsmoment und Querschnittsfläche:
Sowohl Flächensteife als auch Flächenträgheitsradius sollten für eine gute Materialausnutzung möglichst groß sein. Dies führt jedoch zu immer größeren, dünnwandigeren Objekten, die dann zunehmend beulgefährdet sind.
Beispiele
Das Polare Trägheitsmoment 2. Grades ist ,
sofern der Bezugspunkt des polaren Flächenmomentes im Schnittpunkt der y- und
z-Achse liegt.
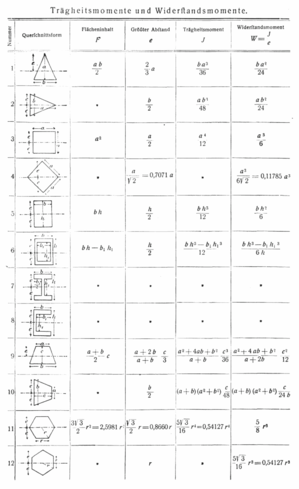
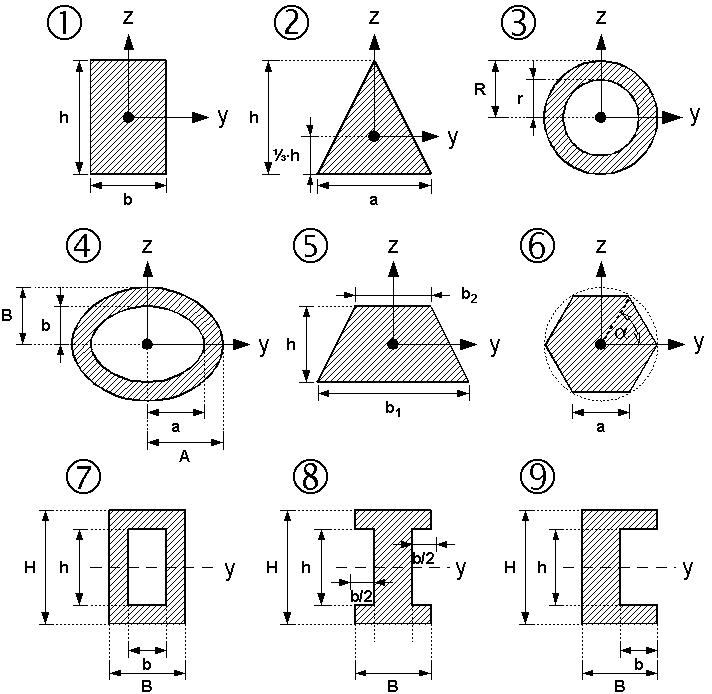
| Nr. | Fläche | Axiales Flächenmoment 2. Grades |
Bemerkungen | |
|---|---|---|---|---|
| um y-Achse | um z-Achse | |||
| 1: Rechteck | Das Quadrat kann als
Spezialfall des Rechtecks mit | |||
| 2: Dreieck | Das oben gezeichnete gleichschenklige Dreieck ist im Allgemeinen nur um die z-Achse symmetrisch | |||
| 3: Kreisring | Der Kreis kann als Spezialfall
des Kreisrings mit | |||
| 4: Ellipsenring | Das Verhältnis Die Ellipse kann als
Spezialfall des Ellipsenringes mit | |||
| 5: Symmetrisches Trapez | ||||
| 6: Regelmäßiges n-Eck | ||||
| 7: Kastenprofil | ||||
| 8: I-Träger
(Doppel-T-Träger) |
||||
| 9: U-Profil | Für den Spezialfall mit gleicher Wandstärke | |||
Weitere Beispiele aus dem Lexikon der gesamten Technik:
Beispiel gerechnet: Flächenträgheitsmoment eines Kreises mit
Radius
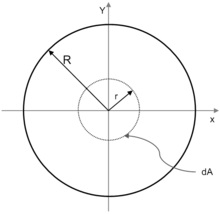
Für den Kreis gilt:
Allgemein gilt:
Daher ergibt sich das axiale Flächenträgheitsmoment eines Kreises zu:
Beispiel gerechnet: Flächenträgheitsmoment eines Rechtecks
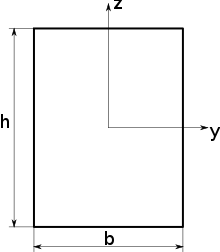
Moment (Integration)
Momente sind in Naturwissenschaften und Technik Kenngrößen einer Verteilung, welche die Lage und Form dieser Verteilung beschreiben. Sie werden durch Integration über die mit einem potenzierten Abstand gewichteten Verteilung berechnet. In diesem Sinne ist das Flächenträgheitsmoment mit dem Massenträgheitsmoment verwandt.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 29.12. 2021