Kreisring
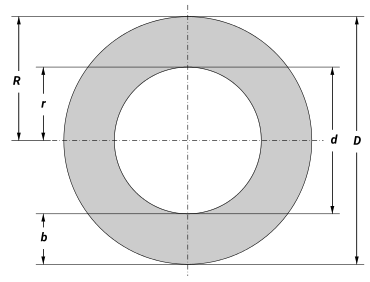
Als Kreisring bezeichnet man die Fläche zwischen zwei konzentrischen Kreisen, d.h. zwischen zwei Kreisen mit gemeinsamem Mittelpunkt. Sein Flächeninhalt beträgt
,
wobei
die Kreiszahl ist und
und
die Radien
sowie
und
die Durchmesser des Außen- bzw.
des Innenkreises bedeuten.
Der Flächeninhalt kann auch aus Innendurchmesser
bzw. Außendurchmesser
und Ringbreite
errechnet werden:
Diese Angaben finden sich z.B. bei Rohrquerschnitten; dabei ist
die Wanddicke.
Ferner lässt sich mit der Kreisringbreite
und mit dem mittleren Kreisringdurchmesser
der Flächeninhalt
berechnen nach
.
Der für hydraulische Anwendungen wirksame hydraulische Durchmesser
bei einem Kreisring beträgt
.
Soll z.B. für Bremsscheiben
ein Reibmoment
und dem Reibwert
nach
bestimmt werden, berechnet sich der reibungsrelevante Radius
bzw. Durchmesser
nach
bzw.
.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.04. 2021