
Zylinder (Geometrie)
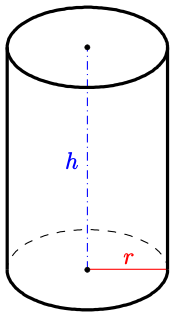
Ein Zylinder (lat. cylindrus, altgriechisch κύλινδρος kýlindros, von κυλίνδειν kylíndein ‚rollen‘, ‚wälzen‘) ist im einfachsten Fall eine
- Fläche, deren Punkte von einer festen Gerade, der Achse, denselben
Abstand
haben.
Da solch eine Fläche unendlich ausgedehnt ist, beschneidet man sie
normalerweise mit zwei parallelen Ebenen der Distanz
(s. Bild).
- Sind die Schnittebenen senkrecht zur Achse, entsteht ein senkrechter
(oder gerader) Kreiszylinder mit Radius
und Höhe
. Die so beschnittene Fläche heißt Mantelfläche des Zylinders, die Schnittflächen senkrecht zur Achse können jeweils als Grundfläche bezeichnet werden.
Da man sich einen geraden Kreiszylinder auch durch Rotation einer Strecke um die (parallele) Zylinderachse erzeugt denken kann, wird er auch Drehzylinder genannt. Die erzeugenden Strecken nennt man Mantellinien des Zylinders oder auch Erzeugende.
In der Technik versteht man unter einem Zylinder oft den Körper, der von der Mantelfläche und den beiden Schnittkreisflächen eingeschlossen wird.
In der Mathematik definiert man einen Zylinder allgemeiner (siehe Abschnitt allgemeiner Zylinder)
Kreiszylinder
In der Praxis spielt der senkrechte Kreiszylinder in verschiedenen Variationen eine wichtige Rolle. Deshalb werden hierfür konkrete Formeln angegeben.
Senkrechter Kreiszylinder

Es ergibt sich für
- das Volumen
(Grundfläche × Höhe)
- die Mantelfläche
(die Abwicklung ist ein Rechteck der Länge
und Höhe
)
- die Oberfläche
Ein gerader Kreiszylinder mit
heißt gleichseitiger Zylinder. Diese Bezeichnung erklärt sich wie folgt:
Schneidet man einen solchen Zylinder mit einer Ebene, die die Zylinderachse
enthält, so erhält man ein Quadrat
(mit der Seitenlänge
).
Ist der Querschnitt eine Ellipse
mit den Halbachsen ,
so ist
Für die Mantelfläche gibt es keine einfache Formel.
Hohlzylinder
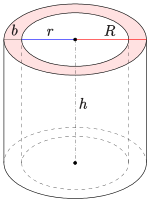
Besitzt ein gerader Kreiszylinder eine Bohrung entlang seiner Achse, so
spricht man von einem Hohlzylinder. Für einen Hohlzylinder – etwa ein
gerades Rohrstück – sind die bestimmenden Größen neben der Höhe
der Außenradius
und der Innenradius
.
Die Wanddicke
b ist somit
.
- Das Volumen ist
- die Mantelfläche (innen und außen)
- die Oberfläche
Ist die Höhe
eines Hohlzylinders kleiner als dessen Außenradius
,
wird von einer Lochscheibe
mit konzentrischer,
kreisförmiger Öffnung gesprochen.
Zylinderabschnitt
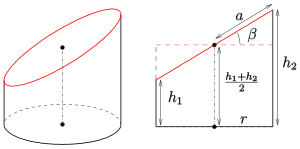
Schneidet man einen geraden Kreiszylinder (Radius )
mit einer Ebene schräg ab, entsteht als Schnittkurve eine Ellipse. Hat der
untere Zylinderabschnitt die minimale Höhe
und die maximale Höhe
,
so hat die Schnittellipse
- die große Halbachse
und die kleine Halbachse
, wobei
ist, mit
dem Neigungswinkel der Schnittebene,
- die numerische
Exzentrizität
.
Der Zylinderabschnitt selbst hat
- das Volumen
,
- die Mantelfläche
- die Oberfläche
.
Bemerkung: Das Volumen und die Mantelfläche sind gleich dem des
Zylinders mit der mittleren Höhe .
Volumenberechnung eines liegenden Kreiszylinders (Tank-Problem)
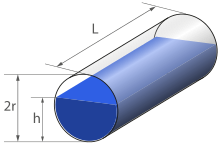
Die Berechnung des Inhalts
eines teilweise gefüllten liegenden Kreiszylinders kann anhand der Länge
,
des Radius
sowie der Füllhöhe
vorgenommen werden. Nach der oben angegebenen Gleichung Volumen =
Grundfläche · Höhe ergibt sich das Volumen der Füllung durch
Multiplikation des Flächeninhalts
des Kreissegments mit der
Länge
des Zylinders:
.
Allgemeiner Zylinder
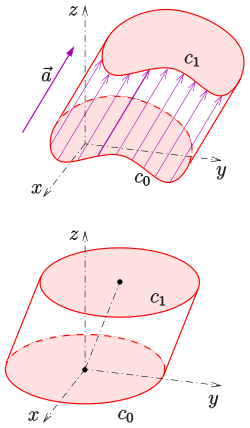
In der Mathematik definiert man einen Zylinder(-Mantel) allgemeiner:
- Eine ebene Kurve
in einer Ebene
wird entlang einer Gerade, die nicht in
enthalten ist, um eine feste Strecke
verschoben. Je zwei sich entsprechenden Punkte der Kurven
und der verschobenen Kurve
werden durch eine Strecke verbunden. Die Gesamtheit dieser parallelen Strecken bildet die zugehörige Zylinder-Fläche (siehe Bild). Die Kurve
nennt man Leitkurve. Eine auf dem Zylinder liegende Gerade heißt Erzeugende oder Mantellinie.
Ist die Kurve ein Kreis, entsteht ein schiefer Kreiszylinder. Falls
ist, ergibt sich ein senkrechter Kreiszylinder.
Ist
eine geschlossene Kurve, kann man die Mantelfläche mit den beiden
Begrenzungsflächen wieder als Oberfläche eines Körpers auffassen. Ist die Kurve
nicht geschlossen, z.B. ein Parabelbogen (siehe unten), so ist der
Zylinder nur die oben erklärte Mantelfläche, die allerdings Teil einer
Oberfläche eines Körpers sein kann.
Die geometrische Besonderheit einer Zylinderfläche besteht in der folgenden Tatsache:
- Eine Zylinderfläche enthält Geraden, sie ist eine Regelfläche, und kann unverzerrt in die Ebene abgewickelt werden.
Insbesondere diese Eigenschaft macht die Zylinderfläche für die Herstellung von Blechverkleidungen interessant.
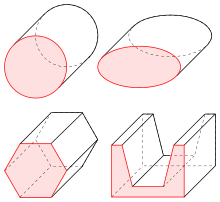
- Ist die erzeugende Kurve ein Polygon, so spricht man von einem Prisma (siehe Beispiele).
Eigenschaften eines allgemeinen Zylinders
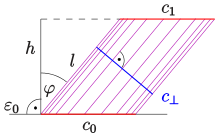
Volumen, Mantelfläche und Oberfläche eines allgemeinen Zylinders berechnen sich wie folgt:
- Volumen:
falls
eine geschlossene Kurve ist,
- wobei
die Grundfläche (von
eingeschlossene Fläche) und
die Höhe ist (siehe Cavalierisches Prinzip).
Bei einem Prisma lässt sich die Grundfläche
entweder direkt (Rechteck) oder durch eine geeignete Zerlegung in Drei- und/oder
Rechtecke berechnen (siehe Flächeninhalt).
Ist
eine stückweise glatte Kurve, kann man durch geeignete Integrale direkt oder
numerisch den Inhalt bestimmen.
- wobei
der Umfang (Bogenlänge) des Querschnitts
(Schnittkurve
zu den Mantellinien) und
die Länge des Mantels ist (siehe Bild). Man beachte:
kann man als senkrechte Parallelprojektion der Leitkurve
auf irgendeine Querschnittsebene (senkrecht zu den Mantellinien) auffassen.
Bei einem senkrechten Zylinder ist
und
die Länge der Leitkurve
.
Bei einem schiefen Zylinder der Höhe
ist
wobei
der Winkel der Zylinderachse (Richtung von
)
und der Normalen der Ebene
ist. Die Querschnittkurve
ist im Falle eines schiefen Kreis- oder elliptischen Zylinders eine Ellipse, bei
einem Prisma ein Polygon. Der Umfang
ist bei einem Polygon einfach die Summe der Kantenlängen, bei einem Kreis
.
Bei einer stückweise glatten Leitkurve
kann man versuchen, die Länge der Querschnittkurve
mit Hilfe eines Kurvenintegrals
zu berechnen. Aber selbst bei einer Ellipse, die kein Kreis ist, ist dies schon
ein Problem (siehe elliptisches
Integral), das man nur numerisch lösen kann.
- Oberfläche:
, falls
eine geschlossene Kurve ist.
Analytische Beschreibung


Die Mantelfläche eines senkrechten Kreiszylinders mit Radius
und Höhe
,
der auf der x-y-Ebene steht und die z-Achse als Achse besitzt, lässt sich durch
eine Gleichung in x,y und eine Ungleichung für z beschreiben:
Will man den Vollzylinder beschreiben, muss man
durch
mit
ersetzen.
Ersetzt man die Kreisgleichung durch die Gleichung einer Ellipse, erhält man die Beschreibung eines senkrechten elliptischen Zylinders:
Das Volumen ist
Eine Parameterdarstellung eines senkrechten Kreis- bzw. elliptischen Zylinders erhält man, in dem man die übliche Parameterdarstellung eines Kreises bzw. einer Ellipse verwendet:
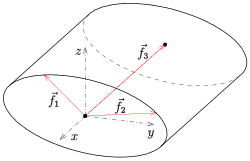
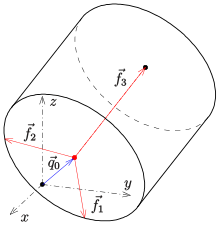
Die Gleichung eines im Raum beliebig gelagerten Zylinders ist schwierig anzugeben. Die Parameterdarstellung eines beliebigen elliptischen Zylinders dagegen relativ einfach:
Dabei ist
der Mittelpunkt der Bodenellipse und
sind drei linear
unabhängige Vektoren.
zeigt in Richtung der Zylinderachse (siehe Bild).
Sind die drei Vektoren
paarweise orthogonal und ist
,
so wird durch die Parameterdarstellung ein senkrechter Kreiszylinder mit Radius
und Höhe
beschrieben (siehe Bild).
Dass ein beliebiger elliptischer Zylinder auch immer Kreise enthält wird in Kreisschnittebene gezeigt.
Diese Art von Parameterdarstellung ist sehr flexibel. z.B. stellt
einen parabolischen Zylinder in allgemeiner Lage dar (siehe Bild, Parabel).
Ein senkrechter parabolischer Zylinder lässt sich analog zum senkrechten Kreiszylinder auch durch
beschreiben.
Die Parameterdarstellung
stellt einen hyperbolischen Zylinder in allgemeiner Lage dar (siehe Hyperbel).
Ein senkrechter hyperbolischer Zylinder lässt sich analog zum senkrechten elliptischen Zylinder durch
beschreiben.
Anwendungsbeispiele
Silo

Getreidesilos haben oft die Form eines Zylinders.
Ein zylinderförmiges Getreidesilo
mit dem Durchmesser 12 Meter und der Höhe 60 Meter wird
zu 40 Prozent mit Weizen gefüllt. Es ist also
und
.
Daraus ergeben sich das Volumen und die Oberfläche:
- Volumen:
- Oberfläche:
Das Getreidesilo wird also mit etwa 2714 Kubikmetern Weizen gefüllt. Die Oberfläche beträgt etwa 1131 Quadratmeter.
Siehe auch
Literatur
- Bronstein-Semendjajew: Taschenbuch der Mathematik. Harri-Deutsch-Verlag, 1983, ISBN 3-87144-492-8.
- Arnfried Kemnitz: Mathematik zum Studienbeginn: Grundlagenwissen für alle technischen, mathematisch-naturwissenschaftlichen und wirtschaftswissenschaftlichen Studiengänge. Springer, 2010, ISBN 978-3-8348-1293-3.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 15.09. 2022