Biegemoment

Biegung eines Stabes (fachsprachlich ein Balken) mit angreifenden „Biegemomenten“ an beiden Enden

Biegung eines durch ein Biegemoment belasteten Balkenstücks
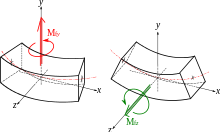
links: Biegung um y-Achse
rechts: Biegung um z-Achse

Das Biegemoment ist das auf die neutrale Faser bezogene, resultierende Moment bei der Biegung von Körpern wie Trägern, Wellen oder Balken, das die Biegespannungen auf den Querschnitt des Körpers ausüben. Es misst also die „Hebelwerkung“, mit der die im Körper auftretenden mechanischen Spannungen einer Biegung entgegenwirken.

Das Biegemoment wird in der SI-Einheit Newtonmeter angegeben.

Biegemoment in der Balkentheorie

Zug- und Druckspannung auf Grund der Belastung eines Kragbalkens nach der Balkentheorie

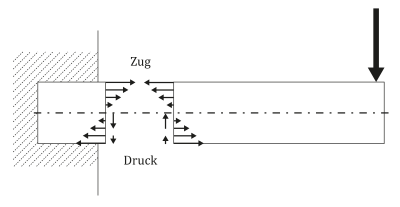
Mit Hilfe der Balkentheorie wird das Verhalten eines Balken unter Belastung beschrieben.

Die für Festigkeitsbetrachtungen erforderliche maximale Biegespannung in einem beliebigen Balkenquerschnitt kann durch die Gleichgewichtsannahme aus dem gegebenen Biegemoment und dem (ev. plastischen) Widerstandsmoment der Querschnittsfläche ermittelt werden.

Bei der Ermittlung der Auswirkungen der Momentbelastungung wird vom Verlauf des Biegemoments über die Balkenlängsrichtung ausgegangen. Im Einzelnen werden die Verformung (Biegelinie) des Balkens und die dabei bestehenden mechanischen Spannungen (Biegespannungen) zum Vergleich mit den zulässigen Spannungen des Balkenmaterials ermittelt.

Beispiele

Biegemoment bei einseitig eingespannten Balken

Eingespannter Balken (Kragbalken) mit einer Kraft F als Punktlast P im Abstand L

Ein einseitig eingespannter Balken wird am freien Ende im Abstand durch eine Kraft belastet. Querschnitt und Materialeigenschaften sind entlang des Balkens konstant. Das Biegemoment ist an der Einleitungsstelle der Kraft gleich Null. Bis zur Einspannstelle steigt es linear auf seinen maximalen Wert an. Der maximale Wert des Biegemoments berechnet sich durch

$M=F\cdot L$

An den Enden abgestützter Balken, mittige Belastung durch Einzelkraft

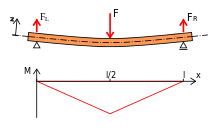
Biegemomentverlauf M(x) über Balken auf zwei Lagern, Einzelkraft F: max. Biegemoment an der Stelle von F

Zur Berechnung der inneren Momente wird das Bauteil an der interessierenden Stelle gedanklich durchgeschnitten und es werden diejenigen Momente betrachtet, die an einem Teilstück in Bezug auf die Schnittstelle wirken. Das Biegemoment an einer Stelle ist damit die Summe aller Drehmomente, die von Kräften auf einer Seite der Schnittstelle verursacht werden.

Im an seinen Enden gelagerten Balken mit mittiger Einzellast (nebenstehende Zeichnung) unterliegt das linke Teilstück einem rechtsdrehenden Drehmoment (in der technischen Mechanik kurz Moment genannt), welches mit Hilfe der Auflagekraft F_L=F/2 am linken Lager beschreibbar ist. Das Moment wächst von Null am Auflager linear bis zum Maximalwert in der Mitte. Rechts der Mitte kommt aus der belastenden Kraft F ein vom Wert Null bis zum gleichen Maximalwert am rechten Auflager linear ansteigendes, linksdrehendes Moment hinzu, so dass die Momenten-Summe vom Maximalwert in der Mitte bis Null am rechten Ende linear abnimmt.^[1]

$M(x)={\begin{cases}F/2\cdot x&{\text{(links der Mitte)}}\\F/2\cdot (l-x)&{\text{(rechts der Mitte)}}\end{cases}}$

In der Mitte des Balkens ( x=l/2 ) ist das Biegemoment maximal und hat den Wert:

$M_{\mathrm {max} }={\frac {F\cdot l}{4}}$

Biegemoment und Biegelinie

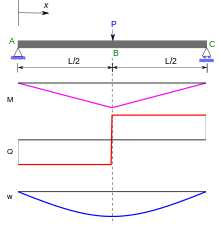
Verlauf eines Biegemoments an einem Balken mit mittiger Kraft F hier als Punktlast P dargestellt, mit dem maximalen Biegemoment M bei l/2 einschließlich des Querkraftverlauf Q und der Biegeline w

→ Hauptartikel: Biegelinie

Die Form beziehungsweise die Biegelinie w(x) eines elastisch verbogenen Bauteiles (Balken) mit konstantem Querschnitt, das einem Biegemoment $M_{y}(x)$ (Index y: Biegung um die y-Achse) unterworfen ist, kann mit folgender Näherungs-Formel beschrieben werden:

$w''(x)=-{M_{y}(x) \over E\cdot I_{y}}$ ( w'' ist die Krümmung der Biegelinie, die in der -Ebene (Bildebene) liegt.)

Der Elastizitätsmodul ist eine Materialeigenschaft, $I_{y}$ ist das axiale Flächenträgheitsmoment (eine rein geometrische Größe) des Balken-Querschnitts, von dem sein Verhalten bei Biegung um die -Achse abhängt.

Die Krümmung w'' ist proportional zum Biegemoment $M_{y}$ .

Im an seinen Enden gelagerten Balken mit mittiger Einzellast (obige Zeichnung) sind beide in der Mitte (x=l/2) am größten.

$w''(x=l/2)=-{F\cdot l \over 4\cdot E\cdot I_{y}}$

Biegemoment und Biegespannung

→ Hauptartikel: Biegespannung

Das Biegemoment folgt aus den Spannungen in Stabachsenrichtung:

$M_{y}=\int \sigma _{xx}\cdot z\cdot \mathrm {d} A$
$M_{z}=\int \sigma _{xx}\cdot y\cdot \mathrm {d} A$

Anmerkungen

↑ Rechts der Mitte führt die spiegelbildliche Betrachtung mit Hilfe der rechten Auflagerkraft F_R über ein linksdrehendes Moment zum gleichen Ergebnis.

Basierend auf einem Artikel in:

Wikipedia.de