Trägheitsmoment

Name

Trägheitsmoment

$I,\,J,\,\Theta$

Größen- und Einheitensystem	Einheit	Dimension
SI	kg·m²	M·L²
cgs	g·cm²	M·L²

Siehe auch: Trägheitstensor

Das Trägheitsmoment, auch Massenträgheitsmoment oder Inertialmoment, gibt die Trägheit eines starren Körpers gegenüber einer Änderung seiner Winkelgeschwindigkeit bei der Drehung um eine gegebene Achse an (Drehmoment geteilt durch Winkelbeschleunigung). Damit spielt es die gleiche Rolle wie die Masse im Verhältnis von Kraft und Beschleunigung; deswegen ist in der älteren Literatur auch die Bezeichnung Drehmasse gebräuchlich. Als physikalische Größe kommt es erstmals 1749 im Werk Scientia Navalis von Leonhard Euler vor.^[1]

Das Trägheitsmoment hängt von der Massenverteilung in Bezug auf die Drehachse ab. Je weiter ein Massenelement von der Drehachse entfernt ist, desto mehr trägt es zum Trägheitsmoment bei; der Abstand geht quadratisch ein. Nimmt die Dichte des Körpers zur Drehachse hin zu, ist sein Trägheitsmoment kleiner, als wenn seine Masse im selben Volumen homogen verteilt wäre. Bei rasch rotierenden Planeten lässt sich deshalb aus der Abplattung auf den Dichteverlauf schließen.

Ist die Drehachse nicht fest vorgegeben, so reicht zur Beschreibung des Trägheitsverhaltens eine einzelne Zahl nicht aus. Aus dem Trägheitstensor kann das Trägheitsmoment für jede beliebige Achse durch den Schwerpunkt berechnet werden.

Anschauliche Beispiele

Balancierhilfe

Hochseilartisten mit Balancierstangen

Beim Seiltanz werden als Balancierhilfe bevorzugt lange Stangen verwendet. Im Vergleich zu einem gleich schweren kompakten Körper, etwa einem Sandsack, hat so eine Stange ein sehr großes Trägheitsmoment. Ein Zur-Seite-Kippen wird dadurch nicht verhindert, aber so verlangsamt, dass der Artist genug Zeit für eine ausgleichende Bewegung hat.

Den Effekt kann man leicht selbst ausprobieren: Ein 30-cm-Lineal (kürzer ist schwieriger) lässt sich hochkant auf der Handfläche balancieren. Quer jedoch, auf eine seiner langen Kanten gestellt, fällt es komplett um, bevor man reagieren kann. Die Drehachse ist in beiden Fällen die aufliegende Kante, während das mittlere Abstandsquadrat von dieser Achse mit über 900 cm² bzw. rund 16 cm² stark verschieden ist.

Dass der Abstand quadratisch in das Trägheitsmoment eingeht, lässt sich leicht einsehen: Eine gegebene Winkelbeschleunigung bedeutet für ein Massenelement in doppeltem Abstand eine doppelt so große tangentiale Beschleunigung und damit eine doppelt so große Trägheitskraft. Das Drehmoment, doppelte Kraft × doppelter Hebelarm, ist damit vierfach so groß.

Drehstuhl und Pirouette

Mit einem weiteren einfachen Experiment kann man eine Änderung des Trägheitsmoments veranschaulichen. Man setzt sich möglichst mittig auf einen drehbaren Bürostuhl und lässt sich mit gestreckten Armen und Beinen in Drehung versetzen. Wenn man dann die Arme und Beine an den Körper heranzieht, nimmt das Trägheitsmoment ab. Das führt dazu, dass die Drehbewegung schneller wird, weil der Drehimpuls erhalten bleibt (siehe Drehimpulserhaltung). Erneutes Ausstrecken verlangsamt die Bewegung wieder. Um den Effekt zu verstärken, kann man in jede Hand schwere Gegenstände nehmen, etwa Hanteln. Je größer deren Masse, desto deutlicher wird der Effekt.

Ein ähnliches Beispiel ist der Pirouetteneffekt, der aus dem Eiskunstlaufen bekannt ist. Die Kontrolle der Drehgeschwindigkeit kann allein aus der Verlagerung der Körpermasse relativ zur Drehachse erfolgen. Zieht der Eiskunstläufer die Arme an oder richtet sich aus einer Hockstellung gerade auf, so dreht er sich schneller – ein erneutes Schwungholen ist nicht nötig.

Formelzeichen und Einheit

Die geläufigsten Formelzeichen für das Trägheitsmoment sind und , zurückgehend auf das lateinische Wort iners, das untätig und träge bedeutet. Da beide Symbole aber auch in der Elektrotechnik Verwendung finden, ist weiterhin ein $\Theta$ (großes Theta) gebräuchlich. In diesem Artikel wird durchgehend verwendet.

Die SI-Einheit des Trägheitsmoments ist kg·m².

Vergleich mit der Masse bei linearer Bewegung

Das Trägheitsmoment bei einer rotierenden Bewegung ist vergleichbar mit der Masse einer linearen (geradlinigen) Bewegung (ausführlich siehe Rotation (Physik)#Vergleich mit der Translationsbewegung). Man vergleiche folgende Gleichungen:

$M=I\cdot \alpha =I\cdot {\ddot {\phi }}$ Rotationsbewegung: Drehmoment = Trägheitsmoment mal Winkelbeschleunigung,

$F=m\cdot a=m\cdot {\ddot {x}}$ Translationsbewegung: Kraft = Masse mal Beschleunigung (Zweites Newtonsches Gesetz).

Allgemeine Definition

Das Massenträgheitsmoment lässt sich bei bekannter Massenverteilung $\rho ({\vec {r}})$ eines Körpers aus folgendem Volumenintegral berechnen:

$I=\int _{V}{\vec {r}}_{\perp }\!^{2}\rho ({\vec {r}})\mathrm {d} V$ .

Dabei ist ${\vec {r}}_{\perp }$ der zur Rotationsachse ${\vec {\omega }}$ (Winkelgeschwindigkeit) senkrechte Vektor von der Achse zum Volumenelement (siehe untenstehende Abbildung).

Motivation der Definition

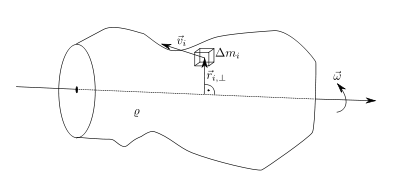
Gezeigt ist eine beliebig geformte Massenverteilung der Dichte $\varrho$ , die um die Achse ${\vec {\omega }}$ rotiert. Ein Massenelement $\Delta m_{i}$ dieser Verteilung hat den Abstand ${\vec {r}}_{i,\perp }$ von der Drehachse und die Bahngeschwindigkeit ${\vec {v}}_{i}$ .

Starrer Körper bestehend aus Massenpunkten

Werden Massenelemente parallel zur Rotationsachse verschoben, ändert sich das Trägheitsmoment nicht. Ein Stab, der den Winkel $\alpha$ mit der Rotationsachse einschließt, wird zerschnitten und die entstandenen Einzelteile parallel zur Rotationsachse so verschoben und zusammengefügt, dass sich ein horizontal gelagerter, kürzerer Stab ergibt. Die Masse, die Massenverteilung und folglich das Trägheitsmoment bezüglich der -Achse bleiben dadurch gleich.

Die gesamte kinetische Energie eines starren Körpers, der aus Massenpunkten besteht, ergibt sich aus der Summe der kinetischen Energien der einzelnen Massenpunkte:

$E_{\mathrm {kin} }=\sum _{i}^{N}{\frac {m_{i}}{2}}v_{i}^{2}$ .

Dabei ist $v_{i}$ die Bahngeschwindigkeit des -ten Massenpunktes. Nun soll der gesamte Körper um die Achse ${\vec {\omega }}$ rotieren. Jeder einzelne Massenpunkt beschreibt daher eine Kreisbahn. Die Bahngeschwindigkeit eines Teilchens, das auf einer Kreisbahn mit Radius mit der Winkelgeschwindigkeit $\omega$ rotiert, lässt sich als $v=\omega \cdot r$ berechnen. Daher folgt:

$E_{\mathrm {rot} }={\frac {1}{2}}\ \underbrace {\left(\sum _{i}^{N}m_{i}r_{i,\perp }^{2}\right)} _{:=I}\ \omega ^{2}$ .

Analog zur Definition der Bewegungsenergie

$E_{\mathrm {kin} }={\frac {1}{2}}\ \underbrace {\left(\sum _{i}^{N}m_{i}\right)} _{=M}\ v^{2}$

eines linear bewegten starren Körpers aus Massenpunkten mit der Gesamtmasse , definiert man das Trägheitsmoment eines rotierenden starren Körpers aus Massenpunkten als

$I=\sum _{i}^{N}m_{i}r_{i,\perp }^{2}$ .

Es gilt also

$E_{\mathrm {rot} }={\frac {1}{2}}I\omega ^{2}$ .

Durch diese Definition kann man folgende Größen rotierender Massenpunkte mit den Größen linear bewegter Massenpunkte identifizieren:

Die Masse eines rotierenden Körpers entspricht dem Trägheitsmoment .
Die Geschwindigkeit eines rotierenden Körpers entspricht der Winkelgeschwindigkeit $\omega$ .

Wählt man die z-Achse des Koordinatensystems in Richtung der Rotationsachse, so lässt sich noch folgende praktische Gleichung ableiten:

$I_{z}=\sum _{i}m_{i}(x_{i}^{2}+y_{i}^{2})$ .

Wobei $x_{i}$ und $y_{i}$ die - und -Koordinaten des -ten Massenpunktes im so gewählten Koordinatensystem sind. Der Index „“ ist wichtig, da das Trägheitsmoment eines Körpers immer auf eine Rotationsachse (hier die -Achse) bezogen ist. Aus der Gleichung ist auch ersichtlich, dass das Trägheitsmoment nicht von den -Koordinaten der einzelnen Massenpunkte abhängt. Das Trägheitsmoment ist unabhängig von den Koordinaten der Massenpunkte in Richtung der Rotationsachse.

Starrer Körper beschrieben durch Massenverteilung

Die Formel für das Massenträgheitsmoment einer allgemeinen Massenverteilung erhält man, indem man sich die Massenverteilung aus vielen kleinen Massenelementen $\Delta m_{i}$ aufgebaut vorstellt. Die Rotationsenergie ist dann näherungsweise durch

$E_{\mathrm {rot} }\approx {\frac {1}{2}}\left(\sum _{i}^{N}\Delta m_{i}r_{i,\perp }^{2}\right)\omega ^{2}$

gegeben. Diese Gleichung wird exakt beim Grenzübergang zu unendlich vielen und unendlich kleinen solchen Massenelementen:

$E_{\mathrm {rot} }=\lim _{N\to \infty ,\,\Delta m_{i}\to 0}{\frac {1}{2}}\left(\sum _{i}^{N}\Delta m_{i}r_{i,\perp }^{2}\right)\omega ^{2}$ ,

oder auch, wenn man die Massen $\Delta m_{i}=\varrho ({\vec {r}}_{i})\Delta V_{i}$ durch die Größe $\Delta V_{i}$ des Volumenelements am Ort ${\vec {r}}_{i}$ und die dort herrschende Massendichte $\varrho ({\vec {r}}_{i})$ ausdrückt:

$E_{\mathrm {rot} }={\frac {1}{2}}\left(\lim _{N\to \infty ,\,\Delta V_{i}\to 0}\sum _{i}^{N}\varrho ({\vec {r}}_{i})\Delta V_{i}\,r_{i,\perp }^{2}\right)\,\omega ^{2}$

Die eingeklammerte Summe ist das Volumenintegral der Funktion $\varrho ({\vec {r}})\,r_{\perp }^{2}$ über das Volumen des aus den infinitesimalen Massenelementen $\mathrm {d} m=\varrho ({\vec {r}})\mathrm {d} V$ zusammengesetzten Körpers.

$E_{\mathrm {rot} }={\frac {1}{2}}\omega ^{2}\int _{V}\mathrm {d} V\,\varrho ({\vec {r}})\,r_{\perp }^{2}={\frac {1}{2}}\omega ^{2}\int _{V}\mathrm {d} m\,r_{\perp }^{2}$

Hieraus ergibt sich die oben angegebene allgemeine Definition des Trägheitsmomentes. Im Falle eines homogenen Körpers, also einer räumlich konstanten Dichte $\rho ({\vec {r}})\equiv \rho$ , vereinfacht sich das zu

$E_{\mathrm {rot} }={\frac {1}{2}}\omega ^{2}\varrho \int _{V}\mathrm {d} V\,\,r_{\perp }^{2}$ .

Zusammenhang zwischen Trägheitsmoment und Drehimpuls

Der Gesamtdrehimpuls ${\vec {L}}$ des starren Körpers zeigt i.d.R. nicht in dieselbe Richtung wie die Winkelgeschwindigkeit ${\vec {\omega }}$ . Die achsenparallele Komponente $L_{\parallel }$ jedoch ist durch $L_{\parallel }=I\omega$ gegeben. Dies lässt sich wie folgt einsehen. Der Ortsvektor eines einzelnen Massenelementes $\Delta m_{i}$ wird nach ${\vec {r}}_{i}={\vec {r}}_{i,\parallel }+{\vec {r}}_{i,\perp }$ in einen zu ${\vec {\omega }}$ parallelen und einen dazu senkrechten Anteil aufgeteilt. Zur achsenparallelen Komponente des Drehimpulses dieses Massenelements $L_{i,\parallel }$ trägt der parallele Anteil des Ortsvektors nichts bei, es bleibt:

${L}_{i,\parallel }=|{\vec {r}}_{i,\perp }\times (\Delta m_{i}{\vec {v}}_{i})|=r_{i,\perp }^{2}\Delta m_{i}\omega$ .

Die achsenparallele Komponente des Gesamtdrehimpulses ergibt sich dann zu

$L_{\parallel }=\sum _{i}L_{i,\parallel }=\omega \sum _{i}r_{i,\perp }^{2}\Delta m_{i}=\omega I$ .

Außerdem folgt daraus sofort $E_{\mathrm {rot} }={\frac {1}{2}}I\omega ^{2}={\frac {L_{\parallel }^{2}}{2I}}$ .

Formeln für wichtige Spezialfälle

Trägheitsmoment eines homogenen rotationssymmetrischen Körpers

Das Trägheitsmoment eines rotationssymmetrischen Körpers, der um seine Symmetrieachse (-Achse) rotiert, kann mit Hilfe von Zylinderkoordinaten berechnet werden.

Ist $r(z)$ der Radius des Körpers bei der Höhe , dann ist das Volumenelement durch eine Kreisscheibe der Dicke $\mathrm {d} z$ gegeben: $\mathrm {d} V=\pi r(z)^{2}\,\mathrm {d} z$ . Daher gilt für einen Körper, der von z=0 bis $z=H$ reicht:

$I={\frac {1}{2}}\pi \rho \int _{0}^{H}r(z)^{4}\,\mathrm {d} z$ .

Ist die Oberfläche des Körpers stattdessen (wie z.B. bei einem Kegel möglich) durch die beim Radius erreichte Höhe $h(r)$ gegeben, kann man das Volumenelement als Mantel eines Zylinders mit Radius so wählen: $\mathrm {d} V=2\pi r\,h(r)\mathrm {d} r$ . Zu integrieren ist dann über alle Radien von r=0 bis zum maximalen Radius r=R

$I=2\pi \rho \int _{0}^{R}r^{3}\,h(r)\,\mathrm {d} r$ .

Trägheitsmomente für zwei zueinander parallele Achsen (Steinerscher Satz)

Illustration der Steiner-Regel. Drehachse 1 geht durch den Schwerpunkt des Körpers der Masse m. Drehachse 2 ist um den Abstand d verschoben.

→ Hauptartikel: Steinerscher Satz

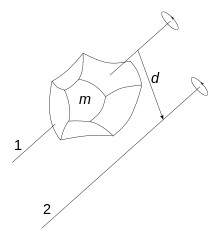
Ist das Trägheitsmoment $I_{{\mathrm {S}}}$ für eine Achse durch den Schwerpunkt eines Körpers bekannt, so ist das Trägheitsmoment $I_{\mathrm {P} }$ für eine beliebige parallel verschobene Drehachse

$\left.I_{\mathrm {P} }=I_{\mathrm {S} }+md^{2}\right.$ .

Dabei gibt den Abstand des Schwerpunkts von der parallel verschobenen Drehachse an.

Man kann den Steinerschen Satz für zwei beliebige parallele Drehachsen verallgemeinern. Dazu muss der Satz zweimal hintereinander angewendet werden: Zunächst verschiebe man die Drehachse so, dass sie durch den Schwerpunkt des Körpers geht, danach auf den gewünschten Zielort.

$I_{\mathrm {neu} }=I_{\mathrm {alt} }+m\left(d_{\mathrm {neu} }^{2}-d_{\mathrm {alt} }^{2}\right)$ .

Satz über zueinander senkrechte Achsen

Dünne Kreisscheibe mit Radius

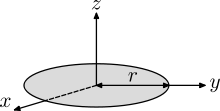
Der Satz über senkrechte Achsen behandelt den Sonderfall einer beliebig geformten Scheibe, deren Dicke im Vergleich zu ihrer Ausdehnung vernachlässigt werden kann. 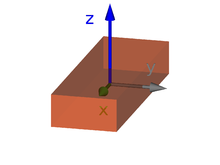Dann ist das Trägheitsmoment um eine beliebige Drehachse senkrecht zur der Scheibenebene gleich der Summe der Trägheitsmomente um zwei beliebige Drehachsen in der Scheibenebene, die zueinander senkrecht sind und deren Schnittpunkt auf der erstgenannten Drehachse liegt. Für einen Körper in der xy-Ebene bei z=0 wie im Bild heißt das:

$I_{z}=I_{x}+I_{y}$ .

Denn dann berechnet sich

$I_{z}=\int \left(x^{2}+y^{2}\right)~\mathrm {d} m=\int x^{2}~\mathrm {d} m+\int y^{2}~\mathrm {d} m=I_{x}+I_{y}$ .

Verallgemeinerung durch Trägheitstensor

→ Hauptartikel: Trägheitstensor

Der Trägheitstensor $\underline {I}$ mit Komponenten $I_{\alpha \beta }\,,\,\alpha ,\beta =1,2,3$ eines Körpers ist eine Verallgemeinerung des Trägheitsmomentes. In einem kartesischen Koordinatensystem lässt sich der Trägheitstensor als Matrix darstellen, die sich aus den Trägheitsmomenten bezüglich der drei Koordinatenachsen und den Deviationsmomenten zusammensetzt. Die drei Trägheitsmomente bilden die Hauptdiagonale der Matrix, die Deviationsmomente sind die Nebendiagonalelemente. Mit Hilfe des Trägheitstensors lässt sich z.B. das Trägheitsmoment bezüglich einer beliebigen durch den Schwerpunkt gehenden Achse berechnen. Wenn ein starrer Körper um eine solche Achse mit der Winkelgeschwindigkeit ${\vec {\omega }}$ rotiert, so ergibt sich das Trägheitsmoment zu

$I={\frac {1}{\omega ^{2}}}\sum _{i=1}^{3}\sum _{j=1}^{3}I_{ij}\;\omega _{i}\;\omega _{j}$

oder in Matrixschreibweise

$I={\frac {1}{\omega ^{2}}}\,{\vec {\omega }}^{T}\cdot {\underline {I}}\cdot {\vec {\omega }}$ .

Drehung des Koordinatensystems

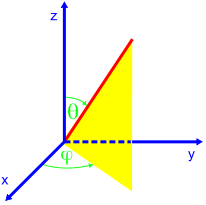
Eine Achse in beliebiger Raumrichtung wird beschrieben durch den Einheitsvektor ${\vec {e}}$ . Man kann diesen z.B. dadurch erhalten, dass man den Einheitsvektor in z-Richtung mittels einer Drehmatrix R dreht:

${\vec {e}}={\underline {R}}\cdot \left({\begin{matrix}0\\0\\1\end{matrix}}\right)$

Mit

${\underline {R}}=\left({\begin{matrix}\cos \varphi \cdot \cos \vartheta &-\sin \varphi &\cos \varphi \cdot \sin \vartheta \\\sin \varphi \cdot \cos \vartheta &\cos \varphi &\sin \varphi \cdot \sin \vartheta \\-\sin \vartheta &0&\cos \vartheta \ \end{matrix}}\right)$

erhält man

${\vec {e}}=\left({\begin{matrix}\cos \varphi \cdot \sin \vartheta \\\sin \varphi \cdot \sin \vartheta \\\cos \vartheta \end{matrix}}\right)$ .

Mit Hilfe dieser Drehmatrix kann nun der Trägheitstensor in ein Koordinatensystem transformiert werden, in dem die z-Achse in Richtung der Rotationsachse zeigt:

${\underline {I'}}={\underline {R}}^{T}\cdot {\underline {I}}\cdot {\underline {R}}$ .

Das Trägheitsmoment für die neue z-Achse ist jetzt einfach das 3. Diagonalelement des Tensors in der neuen Darstellung. Nach Ausführung der Matrizenmultiplikation und trigonometrischen Umformungen ergibt sich

${\begin{aligned}I=&(I_{xx}\cos ^{2}\varphi +I_{yy}\sin ^{2}\varphi +I_{xy}\sin 2\varphi )\sin ^{2}\vartheta \\&+I_{zz}\cos ^{2}\vartheta +(I_{yz}\sin \varphi +I_{zx}\cos \varphi )\sin 2\vartheta \end{aligned}}$ .

Beispielrechnung: Rotationssymmetrischer Körper

Wir betrachten als Beispiel dazu den Trägheitstensor eines rotationssymmetrischen Körpers. Wenn eine der Koordinatenachsen (hier die z-Achse) mit der Symmetrieachse zusammenfällt, dann ist dieser Tensor diagonal. Die Trägheitsmomente für Rotation um die x-Achse und die y-Achse sind gleich ( $I_{xx}=I_{yy}=I_{1}$ ). Für die z-Achse kann das Trägheitsmoment verschieden sein ( $I_{zz}=I_{2}$ ). Der Trägheitstensor hat damit folgende Gestalt:

${\underline {I}}=\left({\begin{matrix}I_{1}&0&0\\0&I_{1}&0\\0&0&I_{2}\end{matrix}}\right)$ .

Transformiert man diesen Tensor wie oben beschrieben in ein Koordinatensystem, das um den Winkel $\vartheta$ um die y-Achse gedreht ist, so erhält man:

${\underline {I'}}=\left({\begin{matrix}I_{1}\cos ^{2}\vartheta +I_{2}\sin ^{2}\vartheta &0&\left(I_{1}-I_{2}\right)\sin \vartheta \cos \vartheta \\0&I_{1}&0\\\left(I_{1}-I_{2}\right)\sin \vartheta \cos \vartheta &0&I_{1}\sin ^{2}\vartheta +I_{2}\cos ^{2}\vartheta \end{matrix}}\right)$ .

Daraus ergibt sich:

Für $I_{1}\neq I_{2}$ sind die Trägheitsmomente für die x- und z-Achse von $\vartheta$ abhängig.
Für $I_{1}\neq I_{2}$ ist der Trägheitstensor nicht mehr diagonal, es treten Deviationsmomente auf.
Das Trägheitsmoment für die neue z-Achse ist: $I=I_{1}\sin ^{2}\vartheta +I_{2}\cos ^{2}\vartheta$ .
Für $I_{1}=I_{2}$ hängt wegen $\sin ^{2}\vartheta +\cos ^{2}\vartheta =1$ das Trägheitsmoment nicht von der Richtung der Drehachse ab.

Besondere Trägheitsmomente

Hauptträgheitsmoment

Die Hauptträgheitsachsen des Quaders: x-Achse das Minimum und z-Achse das Maximum und senkrecht dazu die resultierende y-Achse

Betrachtet man einen beliebig geformten Körper, der um eine Achse durch seinen Massenmittelpunkt rotiert, so variiert dessen Trägheitsmoment je nach Lage dieser Drehachse. Dabei gibt es – im Allgemeinen – eine Achse, bezüglich der das Trägheitsmoment des Körpers maximal anliegt, und eine, für das es minimal anliegt. Diese beiden Achsen stehen immer senkrecht zueinander und bilden zusammen mit einer dritten, wiederum senkrecht auf den beiden anderen stehenden Achse, die Hauptträgheitsachsen oder kurz Hauptachsen des Körpers.

In einem von den Hauptträgheitsachsen aufgespannten Koordinatensystem (Hauptträgheitssystem oder Hauptachsensystem genannt) ist der Trägheitstensor diagonal. Die zu den Hauptträgheitsachsen gehörenden Trägheitsmomente sind also die Eigenwerte des Trägheitstensors, sie heißen Hauptträgheitsmomente.

Ist wie im Bild ein kartesisches Koordinatensystem im Massenmittelpunkt parallel zum Hauptträgheitssystem ausgerichtet, dann berechnen sich die Hauptträgheitsmomente zu:

${\begin{aligned}I_{1}=&\int _{V}(x_{2}^{2}+x_{3}^{2})\,\varrho \mathrm {d} V\\I_{2}=&\int _{V}(x_{3}^{2}+x_{1}^{2})\,\varrho \mathrm {d} V\\I_{3}=&\int _{V}(x_{1}^{2}+x_{2}^{2})\,\varrho \mathrm {d} V\end{aligned}}$

wenn, wie üblich, die Koordinaten nach dem Schema x→x₁, y→x₂ und z→x₃ nummeriert werden.

Mit dem Binet’schen Trägheitsmoment (nach Jacques Philippe Marie Binet)

$i_{\alpha }:=\int _{V}x_{\alpha }^{2}\,\varrho \mathrm {d} V>0\quad {\text{mit}}\quad \alpha =1,2,3$

sind die Hauptträgheitsmomente auch darstellbar als:

${\begin{aligned}I_{1}&=i_{2}+i_{3}\\I_{2}&=i_{3}+i_{1}\\I_{3}&=i_{1}+i_{2}\end{aligned}}$

Daraus ergibt sich:

${\begin{aligned}I_{1}+I_{2}&=i_{1}+i_{2}+2i_{3}=I_{3}+2i_{3}>I_{3}\\I_{2}+I_{3}&=2i_{1}+i_{2}+i_{3}=I_{1}+2i_{1}>I_{1}\\I_{3}+I_{1}&=i_{1}+2i_{2}+i_{3}=I_{2}+2i_{2}>I_{2}\,.\end{aligned}}$

Die Summe zweier Hauptträgheitsmomente ist immer größer als das dritte; sie erfüllen die Dreiecksungleichungen.

Die Hauptträgheitsachsen fallen bei homogener Massenverteilung mit eventuell vorhandenen Symmetrieachsen des Körpers zusammen.

Sind zwei Hauptträgheitsmomente gleich groß, so wird der starre Körper symmetrischer Kreisel genannt. Alle Drehachsen in der Äquatorebene, die von den zugehörigen Hauptträgheitsachsen aufgespannt wird, sind ebenfalls Hauptträgheitsachsen mit dem gleichen Trägheitsmoment. Das ist bei zylindersymmetrischen Körpern unmittelbar klar, gilt aber z.B. ebenso für einen Stab mit quadratischer oder hexagonaler Grundfläche.

Für den Fall, dass alle drei Hauptträgheitsmomente identisch sind, ist, wie oben gezeigt wurde, jede Drehachse durch den Massenmittelpunkt eine Hauptträgheitsachse mit dem gleichen Trägheitsmoment. Dies gilt für alle regelmäßigen Körper wie Kugel, gleichseitiges Tetraeder, Würfel usw.

Zwei Hauptachsen spannen eine Hauptebene auf.

Siehe auch: Trägheitsellipsoid

Trägheitsmoment zur eingespannten Achse

Wenn ein starrer Körper um eine fest eingespannte Achse mit der Winkelgeschwindigkeit ${\vec {\omega }}$ rotiert (die Richtung des Vektors ${\vec {\omega }}$ ist die Richtung der Drehachse), so lässt sich der Drehimpuls ${\vec {L}}$ aus der allgemeinen Formel ${\vec {L}}=I{\vec {\omega }}$ berechnen. Dabei ist im Gegensatz zur oben angegebenen Formel nicht das Trägheitsmoment, sondern der Trägheitstensor. Im Allgemeinen hat der Drehimpuls ${\vec {L}}$ jetzt nicht die Richtung der Drehachse ${\vec {\omega }}$ und ist zeitlich nicht konstant, so dass die Lager ständig Drehmomente aufbringen müssen (dynamische Unwucht). Nur bei Rotation um eine der Hauptträgheitsachsen ist ${\vec {L}}\parallel {\vec {\omega }}$ .

Für die Drehimpulskomponente entlang der Drehachse gilt $L=I\omega$ , dabei ist $\omega$ die Winkelgeschwindigkeit und das Trägheitsmoment bezüglich der Drehachse ${\vec {\omega }}$ . Die kinetische Energie der Rotation, auch kurz als Rotationsenergie bezeichnet, kann durch

$E_{\mathrm {rot} }={\frac {1}{2}}I\omega ^{2}={\frac {L^{2}}{2I}}$

ausgedrückt werden. Diese Formeln zeigen die Analogie zu den entsprechenden Formeln für Impuls und kinetische Energie der Translationsbewegung.

Beispiele

Trägheitsmomente von Himmelskörpern

Fast alle größeren Körper im Weltall (Sterne, Planeten) sind annähernd kugelförmig und rotieren mehr oder weniger schnell. Das Trägheitsmoment um die Rotationsachse ist immer das größte des jeweiligen Himmelskörpers.

Die Differenz dieses „polaren“ und des äquatorialen Trägheitmoments hängt mit der Abplattung des Körpers zusammen, also seiner Verformung der reinen Kugelgestalt durch die Fliehkraft der Rotation. Bei der Erde liegt die Differenz dieser zwei Hauptträgheitsmomente bei 0,3 Prozent, entspricht also etwa der Erdabplattung von 1:298,24. Beim rasch rotierenden Jupiter ist die Differenz und die Abplattung rund 20-mal größer.

Hauptträgheitsmomente einfacher geometrischer Körper mit konstanter Dichte

Wenn nicht ausdrücklich anders angegeben, liegt der Schwerpunkt der geometrischen Körper auf der Drehachse, auf die sich das Trägheitsmoment bezieht. ist die Masse des rotierenden Körpers. Das Trägheitsmoment für Drehungen um andere Achsen kann man dann mit Hilfe des Satzes von Steiner berechnen.

Abbildung	Beschreibung	Trägheitsmoment
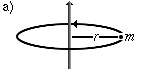	Eine Punktmasse im Abstand um eine Drehachse.	$I=m\,r^{2}$
b)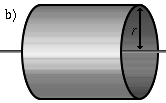	Ein Zylindermantel, der um seine Symmetrieachse rotiert, für eine Wandstärke $d\ll r$ .	$I\approx m\,r^{2}$
c)	Ein Vollzylinder, der um seine Symmetrieachse rotiert.	$I={\frac {1}{2}}m\,r^{2}$
d)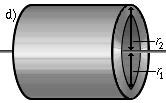	Ein Hohlzylinder, der um seine Symmetrieachse rotiert. Schließt die vorgenannten Grenzfälle Zylindermantel und Vollzylinder mit ein.	$I=m{\frac {r_{1}^{2}+r_{2}^{2}}{2}}$
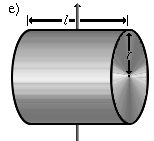	Ein Vollzylinder, der um eine Querachse (zweizählige Symmetrieachse) rotiert.	$I={\frac {1}{4}}m\,r^{2}+{\frac {1}{12}}m\,l^{2}$
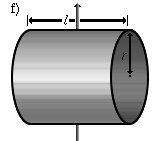	Ein Zylindermantel, der um eine Querachse (zweizählige Symmetrieachse) rotiert.	$I={\frac {1}{2}}m\,r^{2}+{\frac {1}{12}}m\,l^{2}$
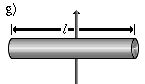	Ein dünner Stab, der um eine Querachse (zweizählige Symmetrieachse) rotiert. Diese Formel ist eine Näherung für einen Zylinder mit $r\ll l$ .	$I={\frac {1}{12}}m\,l^{2}$
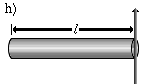	Dünner Stab, der um eine Querachse durch ein Ende rotiert. Diese Formel ist die Anwendung der Steiner-Regel auf den Fall g).	$I={\frac {1}{3}}m\,l^{2}$
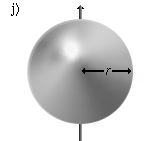	Eine massive Kugel, die um eine Achse durch den Mittelpunkt rotiert.	$I={\frac {2}{5}}m\,r^{2}$
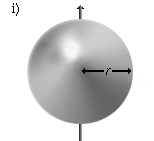	Eine Kugelschale, die um eine Achse durch den Mittelpunkt rotiert, für eine Wandstärke $d\ll r$ .	$I\approx {\frac {2}{3}}m\,r^{2}$
	Eine Hohlkugel, die um eine Achse durch den Mittelpunkt rotiert, für wesentliche Wandstärke mit $d=r_{a}-r_{i}$	$I={\frac {2}{5}}m\,{\frac {r_{a}^{5}-r_{i}^{5}}{r_{a}^{3}-r_{i}^{3}}}$
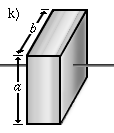	Ein Quader, der um eine Achse durch den Mittelpunkt rotiert, die parallel zu seinen Kanten c liegt.	$I={\frac {1}{12}}m\,(a^{2}+b^{2})$
	Ein massiver Kegel, der um seine Achse rotiert.	$I={\frac {3}{10}}m\,r^{2}$
	Ein Kegelmantel, der um seine Achse rotiert. Die Gleichheit mit dem Trägheitsmoment eines Vollzylinders kann man sich so vorstellen, dass man jeden Kegelmantel zu einer Kreisscheibe „plattdrücken“ kann, ohne sein Trägheitsmoment zu verändern.	$I={\frac {1}{2}}m\,r^{2}$
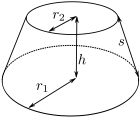	Ein massiver Kegelstumpf, der um seine Achse rotiert.	$I={\frac {3}{10}}m\,{\frac {(r_{1}^{5}-r_{2}^{5})}{(r_{1}^{3}-r_{2}^{3})}}$
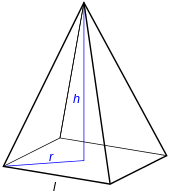	Eine vierseitige, regelmäßige, massive Pyramide, die um ihre Symmetrieachse rotiert.	$I={\frac {1}{5}}m\,r^{2}={\frac {1}{10}}ml^{2}$
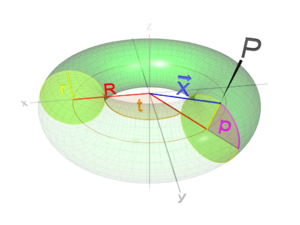	Volltorus mit dem Radius (rot) und der halben Dicke (gelb), der um die Symmetrieachse rotiert. (Der Radius ist so gemeint, dass der Außenradius des Torus ergibt)	$I=m\left({\frac {3}{4}}\,r^{2}+R^{2}\right)$

Beispielrechnung: Trägheitsmoment der homogenen Vollkugel

Zum Verständnis dieses Abschnittes sind grundlegende Kenntnisse der Integralrechnung und Koordinatentransformation hilfreich.

Um das Trägheitsmoment einer massiven homogenen Kugel bezüglich einer Drehachse durch den Kugelmittelpunkt zu berechnen, wird das im Abschnitt „Berechnung“ angegebene Integral verwendet. Der Einfachheit halber soll der Kugelmittelpunkt im Ursprung eines kartesischen Koordinatensystems liegen und die Drehachse entlang der -Achse verlaufen. Um das Integral

$I=\rho \int _{V}(x^{2}+y^{2})\,\mathrm {d} V$

auszuwerten, empfiehlt es sich statt kartesischen lieber Kugelkoordinaten zu verwenden. Beim Übergang müssen dabei die kartesischen Koordinaten x, y, z und das Volumenelement dV durch die Kugelkoordinaten $r,\vartheta ,\varphi$ ausgedrückt werden. Das geschieht mithilfe der Ersetzungsregeln

$x=r\sin \vartheta \cos \varphi$

$y=r\sin \vartheta \sin \varphi$

$z=r\cos \vartheta$

und der Funktionaldeterminanten

$\mathrm {d} V=r^{2}\sin \vartheta \,\mathrm {d} r\,\mathrm {d} \vartheta \,\mathrm {d} \varphi$ .

Einsetzen in den Ausdruck für das Trägheitsmoment liefert

$I=\rho \int _{0}^{R}\!\mathrm {d} r\,\int _{0}^{\pi }\!\mathrm {d} \vartheta \,\int _{0}^{2\pi }\!\mathrm {d} \varphi \;\;r^{4}\sin ^{3}\vartheta$ .

Hier zeigt sich der Vorteil der Kugelkoordinaten: Die Integralgrenzen hängen nicht voneinander ab. Die beiden Integrationen über r und $\varphi$ lassen sich daher elementar ausführen. Das verbleibende Integral in

$I={\frac {2}{5}}\pi \rho R^{5}\int _{0}^{\pi }\sin ^{3}\vartheta \,\mathrm {d} \vartheta$

kann durch Substitution $u=\cos \vartheta ,~du=-\sin \vartheta d\vartheta$ gelöst werden:

$\int _{0}^{\pi }\sin ^{3}\vartheta \,\mathrm {d} \vartheta ={\frac {4}{3}}$ .

Für das Trägheitsmoment ergibt sich schließlich:

$I={\frac {2}{5}}\cdot {\frac {4}{3}}\pi \rho R^{5}={\frac {2}{5}}\rho VR^{2}={\frac {2}{5}}mR^{2}$ .

Messung

Zur Messung eines Trägheitsmoments eines Körpers verwendet man einen Drehtisch. Dieser besteht aus einer Kreisscheibe, die um ihre Symmetrieachse drehbar ist und einer Schneckenfeder (Spiralfeder). Sie bewirkt bei einer Drehung der Scheibe ein rücktreibendes Drehmoment , das direkt proportional zum Auslenkwinkel $\varphi$ ist: $D=-D_{r}\varphi$ . Die Proportionalitätskonstante $D_{r}$ nennt man Direktionsmoment oder Richtmoment. Ihr Wert hängt von der Stärke der Feder ab. Die Scheibe führt nun harmonische Schwingungen mit der Schwingungsdauer

$T_{0}=2\pi {\sqrt {\frac {I_{0}}{D_{r}}}}$ ,

aus, wobei $I_{0}$ das Trägheitsmoment der Scheibe ist. Legt man nun zusätzlich einen Körper mit bekanntem Trägheitsmoment $I_{1}$ auf die Scheibe, so ändert sich die Schwingungsdauer zu

$T_{1}=2\pi {\sqrt {\frac {I_{0}+I_{1}}{D_{r}}}}$ .

Aus der Differenz der Quadrate der jeweiligen Schwingungsdauer

$T_{1}^{2}-T_{0}^{2}=4\pi ^{2}{\frac {I_{1}}{D_{r}}}$

lässt sich das Direktionsmoment $D_{r}$ des Drehtisches bestimmen und aus obiger Formel für $T_{0}$ erhält man dann das Trägheitsmoment $I_{0}$ des Drehtisches. Legt man nun einen beliebigen Körper auf den Drehtisch, so kann man sein Trägheitsmoment bezüglich der Rotationsachse aus der gemessenen Schwingungsdauer

$T=2\pi {\sqrt {\frac {I_{0}+I}{D_{r}}}}$

berechnen.

Moment (Integration)

Momente sind in Naturwissenschaften und Technik Kenngrößen einer Verteilung, welche die Lage und Form dieser Verteilung beschreiben. Sie werden durch Integration über die mit einem potenzierten Abstand gewichtete Verteilung berechnet. In diesem Sinne ist das Massenträgheitsmoment mit dem Flächenträgheitsmoment verwandt.

Anmerkungen

↑ Das Trägheitsmoment wird erstmals dort in Band 1 (§165, S. 70) von Euler explizit definiert, um einen einfachen Ausdruck für die Momentenwirkung träger Massenelemente bei Drehungen um eine feste Achse zu erhalten. Die Vorstellung, dass Materie eine Momentenwirkung hat, die zum Produkt aus der Masse des jeweiligen Körperelementes und zu dem zur Drehachse senkrechten Abstandsquadrat proportional ist, geht allerdings weiter zurück. Sie ist sowohl in früheren Schriften Eulers als auch in denen seiner Vorgänger zu finden, die sich mit Problemen des Schwingungsmittelpunktes zusammengesetzter Körperelemente beschäftigten. Eine erste umfassende Theorie der starren Körper und ihrer Trägheitsmomente publizierte Euler 1765 in Theoria motus corporum solidorum seu rigidorum. Siehe dazu Paul Stäckel: Elementare Dynamik der Punktsysteme und starren Körper. In: F. Klein, C. Müller (Hrsg.): Encyklopädie der Mathematischen Wissenschaften, Band 4 (Mechanik), Heft 4, Leipzig 1908. S. 542–547.

Literatur

Paul A. Tipler: Physik. 3. korrigierter Nachdruck der 1. Auflage 1994, Spektrum Akademischer Verlag Heidelberg Berlin, 2000, ISBN 3-86025-122-8.
Torsten Fließbach: Mechanik. 3. Auflage. Spektrum Akademischer Verlag, Heidelberg 1999, ISBN 3-8274-0546-7.
Wolfgang Demtröder: Experimentalphysik 1. 5. neu bearbeitete und aktualisierte Auflage, Springer-Verlag Berlin Heidelberg, 2008, ISBN 978-3-540-79294-9.

Basierend auf einem Artikel in:

Wikipedia.de