Trägheitsellipsoid

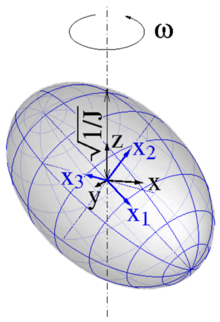
Abb. 1: Trägheitsellipsoid (blaues Netz) und Hauptträgheitsachsen (blau gestrichelt) eines Körpers (nicht dargestellt) und eine Drehachse in globaler -Richtung (schwarz strichpunktiert)

Das Trägheitsellipsoid eines starren Körpers ist eine geschlossene Fläche in Form eines Ellipsoids, die vom Mittelpunkt aus in jeder Richtung einen Abstand hat, der ein Maß für das Trägheitsmoment des Körpers bei Drehung um diese Richtung ist: Das Trägheitsmoment ist gleich dem Kehrwert des Quadrats des Abstands (siehe Abb. 1). Infolgedessen sind die drei Halbachsen des Trägheitsellipsoids zu den Hauptträgheitsachsen des Körpers parallel, und ihre Längen sind durch den Kehrwert der Wurzel aus den entsprechenden Hauptträgheitsmomenten gegeben.

Das Trägheitsellipsoid ist nützlich bei der Betrachtung der Trägheitseigenschaften des Körpers bei Drehbewegungen um eine beliebige Achse. In einem körperfesten Koordinatensystem bleibt es konstant, d.h., es dreht sich immer mit dem Körper mit.

Berechnung

Wie jedem symmetrischen Tensor 2. Stufe in drei Dimensionen kann dem Trägheitstensor Θ eine Fläche zugeordnet werden. Sie wird durch die Endpunkte der Vektoren ${\vec {x}}$ gebildet, die folgende Gleichung erfüllen:

${\begin{aligned}1={\vec {x}}\cdot \mathbf {\Theta } \cdot {\vec {x}}=&{\begin{pmatrix}x\\y\\z\end{pmatrix}}\cdot {\begin{pmatrix}\Theta _{xx}&\Theta _{xy}&\Theta _{xz}\\\Theta _{xy}&\Theta _{yy}&\Theta _{yz}\\\Theta _{xz}&\Theta _{yz}&\Theta _{zz}\end{pmatrix}}\cdot {\begin{pmatrix}x\\y\\z\end{pmatrix}}\\=&\Theta _{xx}x^{2}+\Theta _{yy}y^{2}+\Theta _{zz}z^{2}+2\Theta _{xy}xy+2\Theta _{xz}xz+2\Theta _{yz}yz\end{aligned}}$

Darin bezeichnen x, y und z die Komponenten des Vektors ${\vec {x}}$ und Θ_{xx, xy, …} die Komponenten des Trägheitstensors bezüglich einer beliebig orientierten Orthonormalbasis. Im Hauptträgheitsachsensystem, kurz Hauptachsensystem, wird der Trägheitstensor diagonal und es entsteht:

${\begin{aligned}1={\vec {x}}\cdot \mathbf {\Theta } \cdot {\vec {x}}=&{\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix}}\cdot {\begin{pmatrix}\Theta _{1}&0&0\\0&\Theta _{2}&0\\0&0&\Theta _{3}\end{pmatrix}}\cdot {\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix}}\\=&\Theta _{1}x_{1}^{2}+\Theta _{2}x_{2}^{2}+\Theta _{3}x_{3}^{2}={\frac {x_{1}^{2}}{{\sqrt {\tfrac {1}{\Theta _{1}}}}^{2}}}+{\frac {x_{2}^{2}}{{\sqrt {\tfrac {1}{\Theta _{2}}}}^{2}}}+{\frac {x_{3}^{2}}{{\sqrt {\tfrac {1}{\Theta _{3}}}}^{2}}}\end{aligned}}$

Die Komponenten x_1,2,3 und die Hauptträgheitsmomente Θ_1,2,3 beziehen sich auf das körperfeste Hauptachsensystem. Der Trägheitstensor ist positiv definit, denn die Rotationsenergie ${\tfrac {1}{2}}{\vec {\omega }}\cdot \mathbf {\Theta } \cdot {\vec {\omega }}$ ist für ${\vec {\omega }}\neq {\vec {0}}$ immer positiv. Daher ist die Fläche ein dreiachsiges Ellipsoid.

In einem Bezugssystem, in dem sich der Körper dreht, sind die Komponenten des Trägheitstensors Θ_{xx, xy,...} von der Zeit abhängig. Das Trägheitsellipsoid bleibt mit dem Körper ausgerichtet. Die sechs unabhängigen Komponenten des Trägheitstensors entsprechen den drei Hauptträgheitsmomenten und der Orientierung der Hauptträgheitsachsen, also der Form und Ausrichtung des Ellipsoids.

Mit dem Trägheitstensor berechnen sich die Trägheitsmomente J bezüglich einer beliebigen Drehachse durch das Ellipsoidzentrum in Richtung des Einheitsvektors ${\hat {e}}$ (der Länge eins und deshalb mit Hut geschrieben) gemäß $J={\hat {e}}\cdot \mathbf {\Theta } \cdot {\hat {e}}$ . Für einen Vektor ${\vec {x}}=x{\hat {e}}$ , der vom Ellipsoidzentrum zum Schnittpunkt der Drehachse mit dem Trägheitsellipsoid weist und den Betrag x hat, ergibt sich

$1={\vec {x}}\cdot \mathbf {\Theta } \cdot {\vec {x}}=x^{2}{\hat {e}}\cdot \mathbf {\Theta } \cdot {\hat {e}}=x^{2}J\quad \rightarrow \quad x={\sqrt {\frac {1}{J}}}\,.$

Die Drehachse schneidet das Ellipsoid also im Abstand ${\sqrt {\tfrac {1}{J}}}$ vom Zentrum des Ellipsoids.

Die Hauptträgheitsmomente Θ_1,2,3 erfüllen die Dreiecksungleichungen. Damit ein Ellipsoid mit den Achsen a, b und c ein Trägheitsellipsoid sein kann, muss sich also aus Strecken der Längen 1/a², 1/b² und 1/c² ein Dreieck formen lassen.

Spezielle Körper

Die Länge der Halbachsen des Trägheitsellipsoids sind umgekehrt proportional zur Wurzel aus den Hauptträgheitsmomenten. Anschaulich entspricht einem in einer Richtung gestreckten Trägheitsellipsoid ein Körper, der in dieser Richtung gestaucht ist, und umgekehrt. Bei homogener Dichteverteilung und Drehung um den Massenmittelpunkt gilt:

Unsymmetrische Kreisel besitzen ein „echtes“ Ellipsoid als Trägheitsellipsoid, da Θ₁ ≠ Θ₂ ≠ Θ₃ ≠ Θ₁. Beispiele sind der Quader mit drei ungleichen Seiten oder gewinkelte Moleküle wie das Wassermolekül H₂O. Das Trägheitsellipsoid eines Ziegelsteins hat die Form eines stark abgerundeten Stücks Seife, das quer zum Ziegelstein liegt (kürzeste Mittelpunktsachse des Ellipsoids parallel zur längsten Symmetrieachse des Körpers, und umgekehrt).
Symmetrische Kreisel besitzen ein Rotationsellipsoid als Trägheitsellipsoid, da zwei Hauptträgheitsmomente gleich sind, z.B. Θ₁ = Θ₂. Bei rotationssymmetrischen Körpern ist die Symmetrieachse stets eine Hauptträgheitsachse, die beiden Hauptträgheitsmomente um beliebige dazu senkrechte Achsen sind gleich. Beispiele: Kreiszylinder, lineare Moleküle.
Auch Körper mit n-zähliger Drehsymmetrie haben ab ein Rotationsellipsoid als Trägheitsellipsoid, denn ein Ellipsoid kann keine Drehsymmetrie höher als wiedergeben. Beispiele: Säulen oder Pyramiden mit gleichseitig-dreieckigem oder quadratischem Querschnitt, also auch Tetraeder etc.
- Beim gestreckten oder prolaten Kreisel ist Θ₁ = Θ₂ > Θ₃ und deshalb ist sein Trägheitsellipsoid ein in der Symmetrieachse ${\hat {e}}_{3}$ langgestrecktes, zigarrenförmiges Rotationsellipsoid.
- Beim abgeplatteten oder oblaten Kreisel ist Θ₁ = Θ₂ < Θ₃ und deshalb ist sein Trägheitsellipsoid ein in der Symmetrieachse ${\hat {e}}_{3}$ gestauchtes Rotationsellipsoid. Beispiele: Puck, näherungsweise die abgeplattete Erde.
Kugelkreisel oder sphärische Kreisel besitzen eine Kugel als Trägheitsellipsoid, da Θ₁ = Θ₂ = Θ₃. Hat ein Körper bezüglich dreier verschiedener Achsen gleiche Trägheitsmomente, so ist das Trägheitsellipsoid eine Kugel. Dies hat zur Folge, dass das Trägheitsmoment bezüglich jeder Achse gleich ist. Die Form des Körpers muss jedoch nicht der einer Kugel entsprechen: bei homogener Dichteverteilung reicht bereits eine Punktsymmetrie wie beim Würfel oder den anderen regelmäßigen Körpern. Zudem können auch unregelmäßig geformte Körper Kugelkreisel sein.

Bei inhomogener Dichteverteilung kann von der äußeren Form nicht ohne Weiteres auf die Form des Trägheitsellipsoids geschlossen werden.

Weitere mit der Drehbewegung verknüpfte Ellipsoide

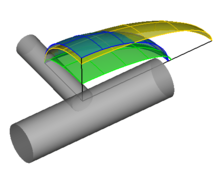
Abb. 2: Starrer Körper (grau) mit Trägheits-, Drall- und Massenellipsoid (blau, gelb bzw. grün), die hier alle auf gleichlange 2-Achsen skaliert sind

Neben dem Trägheitsellipsoid sind noch weitere Ellipsoide für die Drehbewegung bedeutsam, siehe Abb. 2:

Das Energieellipsoid, das auch „Poinsotellipsoid“ oder „Poinsotfläche“ nach Louis Poinsot genannt wird, beinhaltet alle Winkelgeschwindigkeiten, die bei einem gegebenen Körper derselben Rotationsenergie entsprechen. Das Energieellipsoid geht aus dem Trägheitsellipsoid durch zentrische Streckung hervor. Die Bewegung kräftefrei drehender, starrer Körper kann mit der Poinsot’schen Konstruktion anhand des Energieellipsoids visualisiert werden.
Das Drallellipsoid ist der geometrische Ort aller Winkelgeschwindigkeiten, die demselben Drehimpulsbetragsquadrat entsprechen. Das Drallellipsoid ist in jeder Hinsicht schlanker als das Trägheitsellipsoid und skaliert mit dem Drehimpulsbetrag. Bei gegebener Rotationsenergie ist die Größe des Drallellipsoids nach unten und oben beschränkt.
Das MacCullagh-Ellipsoid ist der geometrische Ort aller Drehimpulse, die derselben Rotationsenergie entsprechen. Das MacCullagh-Ellipsoid ist in gewisser Weise reziprok zum Energieellipsoid, denn einander entsprechende Achsen haben einander reziproke Längen. Ein abgeplattetes MacCullagh-Ellipsoid gehört zu einem gestreckten Energieellipsoid und umgekehrt.
Das Massenellipsoid ist ein homogener, ellipsoidförmiger Körper, der die gleiche Masse und das gleiche Trägheitsellipsoid wie ein vorgegebener Körper besitzt.

Trägheits- und Massenellipsoid sind im körperfesten System von eventuell auftretenden Bewegungen unbeeinflusste Eigenschaften eines (starren) Körpers allein, sind sich aber ansonsten im Allgemeinen nicht ähnlich. Alle diese Ellipsoide sind mit dem Körper ausgerichtet mit seinen Hauptträgheitsachsen als Symmetrieachsen.

Energieellipsoid

Das Energieellipsoid für eine gegebene Rotationsenergie hat die gleiche geometrische Gestalt und Orientierung wie das Trägheitsellipsoid, wobei der Abstand der Punkte auf dem Energieellipsoid vom Mittelpunkt nun durch den Betrag der Winkelgeschwindigkeit gegeben ist, die zu dieser Rotationsenergie gehört. Diese Fläche wird durch die Endpunkte der Vektoren ${\vec {\omega }}$ gebildet, die bei festgehaltener Rotationsenergie E_rot folgender Gleichung genügen:

$E_{\text{rot}}={\frac {1}{2}}{\vec {\omega }}\cdot \mathbf {\Theta } \cdot {\vec {\omega }}$

Diese Fläche stimmt mit einem um den Faktor ${\sqrt {2E_{\text{rot}}}}$ gestreckten Trägheitsellipsoid überein, denn die definierenden Formeln gehen ineinander über, wenn ${\vec {\omega }}={\sqrt {2E_{\text{rot}}}}{\vec {x}}$ eingesetzt wird.

In einem kartesischen Koordinatensystem mit xyz-Achsen komponentenweise ausgeschrieben lautet die Gleichung

${\begin{aligned}E_{\text{rot}}=&{\frac {1}{2}}{\begin{pmatrix}\omega _{x}\\\omega _{y}\\\omega _{z}\end{pmatrix}}\cdot {\begin{pmatrix}\Theta _{xx}&\Theta _{xy}&\Theta _{xz}\\\Theta _{xy}&\Theta _{yy}&\Theta _{yz}\\\Theta _{xz}&\Theta _{yz}&\Theta _{zz}\end{pmatrix}}\cdot {\begin{pmatrix}\omega _{x}\\\omega _{y}\\\omega _{z}\end{pmatrix}}\\=&{\frac {1}{2}}(\Theta _{xx}\omega _{x}^{2}+\Theta _{yy}\omega _{y}^{2}+\Theta _{zz}\omega _{z}^{2}+2\Theta _{xy}\omega _{x}\omega _{y}+2\Theta _{xz}\omega _{x}\omega _{z}+2\Theta _{yz}\omega _{y}\omega _{z})\\=:&f({\vec {\omega }})\,.\end{aligned}}$

Im Hauptachsensystem vereinfacht sich diese quadratische Form (wobei ω_1,2,3} die Komponenten der Winkelgeschwindigkeit ${\vec {\omega }}$ im Hauptträgheitssystem sind) zu

$E_{\text{rot}}={\frac {1}{2}}(\Theta _{1}\omega _{1}^{2}+\Theta _{2}\omega _{2}^{2}+\Theta _{3}\omega _{3}^{2})$

oder umgeformt zu

$1={\frac {\omega _{1}^{2}}{{\sqrt {\tfrac {2E_{\text{rot}}}{\Theta _{1}}}}^{2}}}+{\frac {\omega _{2}^{2}}{{\sqrt {\tfrac {2E_{\text{rot}}}{\Theta _{2}}}}^{2}}}+{\frac {\omega _{3}^{2}}{{\sqrt {\tfrac {2E_{\text{rot}}}{\Theta _{3}}}}^{2}}}\,.$

Poinsotsche Konstruktion der Richtung des Drehimpulses

Betrachtet man die Rotationsenergie E_rot als Funktion im dreidimensionalen Raum der Winkelgeschwindigkeiten ${\vec {\omega }}$ , dann ist der Drehimpuls ${\vec {L}}$ gerade der Gradient dieser Funktion. Im Hauptachsensystem mit den Basisvektoren ${\hat {e}}_{k}$ gilt nämlich

$\operatorname {grad} _{\vec {\omega }}(E_{\text{rot}})\,=\,{\begin{pmatrix}{\frac {\partial E_{\text{rot}}}{\partial \omega _{1}}}&{\frac {\partial E_{\text{rot}}}{\partial \omega _{2}}}&{\frac {\partial E_{\text{rot}}}{\partial \omega _{3}}}\end{pmatrix}}\,=\,\Theta _{1}\omega _{1}{\hat {e}}_{1}+\Theta _{2}\omega _{2}{\hat {e}}_{2}+\Theta _{3}\omega _{3}{\hat {e}}_{3}\ =\,{\vec {L}}\ .$

Da der Gradient einer Funktion an jedem Punkt senkrecht auf der Fläche konstanten Funktionswerts steht, ist der zu einer Winkelgeschwindigkeit ${\vec {\omega }}$ gehörende Drehimpuls parallel zur Senkrechten auf dem Energieellipsoid an der Stelle ${\vec {\omega }}$ .

Abb. 3: Schnitt durch ein Energieellipsoid entlang zweier Hauptträgheitsachsen, mit den Hauptträgheitsmomenten Θ₁ und Θ₂

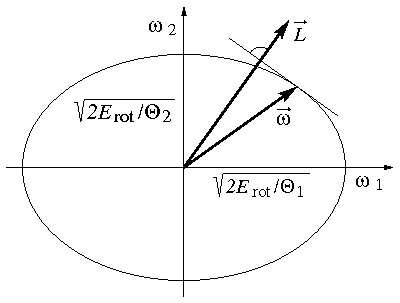
Der Drehimpuls ist also parallel zur Normalen des Energieellipsoids in dem Punkt, an dem die Spitze des Winkelgeschwindigkeitsvektors das Ellipsoid berührt (siehe Abb. 3). Damit ist ersichtlich, dass

${\vec {\omega }}$ und ${\vec {L}}$ nur entlang der Hauptträgheitsachsen parallel sind,
Drehimpuls und Winkelgeschwindigkeit immer einen spitzen Winkel (< 90°) einschließen, denn $2E_{\text{rot}}={\vec {\omega }}\cdot {\vec {L}}>0$ , und
der Zuwachs an Rotationsenergie maximal ist, wenn die Winkelgeschwindigkeit in Richtung des Drehimpulses zunimmt, denn $\mathrm {d} E_{\text{rot}}={\vec {L}}\cdot \mathrm {d} {\vec {\omega }}$ .

Im kräftefreien Fall sind der Drehimpuls und die Rotationsenergie konstant und wegen $2E_{\text{rot}}={\vec {\omega }}\cdot {\vec {L}}$ ist auch die Komponente der Winkelgeschwindigkeit in Richtung des Drehimpulses konstant. Die Tangentialebene an das Energieellipsoid am Ort der aktuellen Winkelgeschwindigkeit ist damit fest und die Winkelgeschwindigkeit bewegt sich auf sogenannten Herpolhodien in dieser Ebene. Im körperfesten Hauptträgheitssystem zeichnet die Winkelgeschwindigkeit „Polhodien“ genannte Kurven nach, die die Schnittmenge von Drehimpuls- und Energieellipsoid sind.

Drallellipsoid

Die Winkelgeschwindigkeiten, die alle dasselbe Drehimpulsbetragsquadrat $L^{2}:={\vec {L}}\cdot {\vec {L}}$ zu einem bestimmten Zeitpunkt liefern, definieren ebenfalls ein Ellipsoid, das Drallellipsoid:

$L^{2}={\vec {\omega }}\cdot \mathbf {\Theta } \cdot \mathbf {\Theta } \cdot {\vec {\omega }}=\Theta _{1}^{2}\omega _{1}^{2}+\Theta _{2}^{2}\omega _{2}^{2}+\Theta _{3}^{2}\omega _{3}^{2}\quad \rightarrow \quad 1={\frac {\omega _{1}^{2}}{\left({\frac {L}{\Theta _{1}}}\right)^{2}}}+{\frac {\omega _{2}^{2}}{\left({\frac {L}{\Theta _{2}}}\right)^{2}}}+{\frac {\omega _{3}^{2}}{\left({\frac {L}{\Theta _{3}}}\right)^{2}}}\,.$

Das Drallellipsoid ist also schlanker als das Trägheitsellipsoid, siehe Abb. 2: $l_{L,i}={\frac {L}{\Theta _{i}}}.$

Die Winkelgeschwindigkeit liegt zu einem bestimmten Zeitpunkt sowohl auf diesem Ellipsoid als auch auf dem Energieellipsoid. Damit beide Ellipsoide gemeinsame Punkte haben können, muss zu jedem Zeitpunkt

$2\Theta _{1}E_{\text{rot}}\leq L^{2}\leq 2\Theta _{3}E_{\text{rot}}$ oder ${\frac {L^{2}}{2\Theta _{3}}}\leq E_{\text{rot}}\leq {\frac {L^{2}}{2\Theta _{1}}}$

gelten, wenn wie üblich die Hauptträgheitsmomente gemäß Θ₁ < Θ₂ < Θ₃ angeordnet sind. Denn ein Punkt, der auf beiden Ellipsoiden liegt, muss die Bedingungen

${\begin{aligned}1=&{\frac {1}{L^{2}}}(\Theta _{1}^{2}\omega _{1}^{2}+\Theta _{2}^{2}\omega _{2}^{2}+\Theta _{3}^{2}\omega _{3}^{2})={\frac {1}{2E_{\text{rot}}}}(\Theta _{1}\omega _{1}^{2}+\Theta _{2}\omega _{2}^{2}+\Theta _{3}\omega _{3}^{2})\\\rightarrow 0=&(2E_{\text{rot}}\Theta _{1}-L^{2})\Theta _{1}\omega _{1}^{2}+(2E_{\text{rot}}\Theta _{2}-L^{2})\Theta _{2}\omega _{2}^{2}+(2E_{\text{rot}}\Theta _{3}-L^{2})\Theta _{3}\omega _{3}^{2}\\=&2\left(E_{\text{rot}}-{\frac {L^{2}}{2\Theta _{1}}}\right)\Theta _{1}^{2}\omega _{1}^{2}+2\left(E_{\text{rot}}-{\frac {L^{2}}{2\Theta _{2}}}\right)\Theta _{2}^{2}\omega _{2}^{2}+2\left(E_{\text{rot}}-{\frac {L^{2}}{2\Theta _{3}}}\right)\Theta _{3}^{2}\omega _{3}^{2}\end{aligned}}$

erfüllen. In den letzten beiden Gleichungen sind alle Faktoren bis auf die Klammerausdrücke null oder positiv. Damit eine nichttriviale Lösung existiert, darf in beiden Gleichungen der kleinste Klammerausdruck nicht positiv und der größte nicht negativ sein. Mit den angenommenen Größenverhältnissen der Hauptträgheitsmomente stellt dies die obigen Schranken für das Drehimpulsbetragsquadrat und die Rotationsenergie sicher. Dann sind die Rotationsenergie und der Drehimpulsbetrag mit einer Drehbewegung des betrachteten Körpers verträglich.

Bei gegebener Rotationsenergie hat eine Drehung um die Hauptträgheitsachse mit dem kleinsten Hauptträgheitsmoment den kleinsten und eine Drehung um die Hauptträgheitsachse mit dem größten Hauptträgheitsmoment den größten Drehimpulsbetrag.

Umgekehrt hat bei gegebenem Drehimpulsbetrag eine Drehung um die Hauptträgheitsachse mit dem kleinsten Hauptträgheitsmoment die größte und eine Drehung um die Hauptträgheitsachse mit dem größten Hauptträgheitsmoment die kleinste Rotationsenergie. Deswegen wird die Drehachse bei dissipativen Vorgängen (Luftwiderstand, Reibung) in Richtung der 3-Achse wandern.

MacCullagh-Ellipsoid

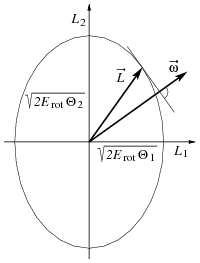
Abb. 4: Schnitt durch ein MacCullagh-Ellipsoid entlang zweier Hauptträgheitsachsen mit den Hauptträgheitsmomenten Θ₁ und Θ₂

Das nach James MacCullagh benannte MacCullagh-Ellipsoid ist der geometrische Ort aller Endpunkte des Drehimpulses ${\vec {L}}$ , die zur selben Rotationsenergie führen. Das MacCullagh-Ellipsoid ist also das Analogon zum Energieellipsoid im Drehimpulsraum:

$E_{\text{rot}}={\frac {1}{2}}{\vec {L}}\cdot \mathbf {\Theta } ^{-1}\cdot {\vec {L}}={\frac {L_{1}^{2}}{2\Theta _{1}}}+{\frac {L_{2}^{2}}{2\Theta _{2}}}+{\frac {L_{3}^{2}}{2\Theta _{3}}},$

wobei in der rechten Gleichung die Hauptachsendarstellung des Drehimpulses benutzt wurde. In diesem System hat das Ellipsoid folglich die Gleichung

$1={\frac {L_{1}^{2}}{{\sqrt {2E_{\text{rot}}\Theta _{1}}}^{2}}}+{\frac {L_{2}^{2}}{{\sqrt {2E_{\text{rot}}\Theta _{2}}}^{2}}}+{\frac {L_{3}^{2}}{{\sqrt {2E_{\text{rot}}\Theta _{3}}}^{2}}}.$

Es ist wie die anderen Ellipsoide körperfest und entlang der Hauptachsen ausgerichtet. Das MacCullagh-Ellipsoid ist gewissermaßen reziprok zum Energieellipsoid, denn das Produkt der Halbachsen des Energieellipsoids $l_{E,i}={\sqrt {\tfrac {2E_{\text{rot}}}{\Theta _{i}}}}$ und des MacCullagh-Ellipsoids $l_{C,i}={\sqrt {2E_{\text{rot}}\Theta _{i}}}$ ist auf allen Hauptachsen gleich:

$l_{E,1}l_{C,1}=l_{E,2}l_{C,2}=l_{E,3}l_{C,3}=2E_{\text{rot}}.$

Bei abgeplattetem Energieellipsoid ist das MacCullagh-Ellipsoid gestreckt und umgekehrt.

Bei der kräfefreien Bewegung eines Starrkörpers ist der Drehimpuls und die Rotationsenergie konstant. Dem Körper sind dann nur solche Drehungen um den Ursprung erlaubt, bei denen der fixe Endpunkt des Drehimpulses sein MacCullagh-Ellipsoid und die Drallkugel mit dem Radius $|{\vec {L}}|$ berührt. Analog zur Poinsot’schen Konstruktion ergibt sich die Winkelgeschwindigkeit als Gradient im Drehimpulsraum:

$\operatorname {grad} _{\vec {L}}(E_{\text{rot}})\,=\,{\begin{pmatrix}{\frac {\partial E_{\text{rot}}}{\partial L_{1}}}&{\frac {\partial E_{\text{rot}}}{\partial L_{2}}}&{\frac {\partial E_{\text{rot}}}{\partial L_{2}}}\end{pmatrix}}\,=\,{\frac {L_{1}}{\Theta _{1}}}{\hat {e}}_{1}+{\frac {L_{2}}{\Theta _{2}}}{\hat {e}}_{2}+{\frac {L_{3}}{\Theta _{3}}}{\hat {e}}_{3}\ =\,{\vec {\omega }}$

Massenellipsoid

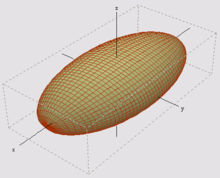
Abb. 5: Ellipsoid mit drei ungleichen Halbachsen

Zu jedem starren Körper gibt es einen ellipsoidförmigen Körper wie in Abb. 5, das Massenellipsoid, das die gleichen Trägheitseigenschaften (Masse und Trägheitstensor) besitzt wie der Körper selbst. Das Massenellipsoid und das Trägheitsellipsoid haben gleiche Symmetrieachsen, sind sich aber ansonsten zumeist nicht ähnlich. Wenn sich nämlich die mittellangen Halbachsen nach geeigneter Skalierung decken, wird die größte Halbachse des Trägheitsellipsoids kleiner, die kleinste aber größer als die entsprechende des Massenellipsoids sein, siehe Abb. 2.

Denn bei homogener Dichteverteilung hat ein ellipsoidförmiger Körper mit Masse sowie den Halbachsen , und in -, - bzw. -Richtung die Hauptträgheitsmomente

${\begin{aligned}\Theta _{x}=&{\frac {m}{5}}(b^{2}+c^{2})\\\Theta _{y}=&{\frac {m}{5}}(a^{2}+c^{2})\\\Theta _{z}=&{\frac {m}{5}}(a^{2}+b^{2})\end{aligned}}$

oder bei gegebenen Hauptträgheitsmomenten die Halbachsen

${\begin{aligned}a=&{\sqrt {{\frac {5}{2m}}(\Theta _{y}+\Theta _{z}-\Theta _{x})}}\\b=&{\sqrt {{\frac {5}{2m}}(\Theta _{x}+\Theta _{z}-\Theta _{y})}}\\c=&{\sqrt {{\frac {5}{2m}}(\Theta _{x}+\Theta _{y}-\Theta _{z})}}\,.\end{aligned}}$

Weil die Hauptträgheitsmomente die Dreiecksungleichungen erfüllen, besitzt jeder Körper ein Massenellipsoid. Anders als beim Trägheitsellipsoid können die Halbachsen des Massenellipsoids jedes Verhältnis zueinander aufweisen, brauchen also nicht die Dreiecksungleichungen zu erfüllen. Die Halbachsen des Trägheitsellipsoids verhalten sich wie

${\frac {1}{\sqrt {\Theta _{z}}}}:{\frac {1}{\sqrt {\Theta _{y}}}}:{\frac {1}{\sqrt {\Theta _{x}}}}={\frac {1}{\sqrt {a^{2}+b^{2}}}}:{\frac {1}{\sqrt {a^{2}+c^{2}}}}:{\frac {1}{\sqrt {b^{2}+c^{2}}}}=\underbrace {\sqrt {\frac {1+{\frac {a^{2}}{c^{2}}}}{1+{\frac {a^{2}}{b^{2}}}}}} _{=:p}c:b:\underbrace {\sqrt {\frac {1+{\frac {c^{2}}{a^{2}}}}{1+{\frac {c^{2}}{b^{2}}}}}} _{=:q}a\,.$

Wenn a>b>c ist, dann ist ${\tfrac {a^{2}}{c^{2}}}>{\tfrac {a^{2}}{b^{2}}}$ und ${\tfrac {c^{2}}{a^{2}}}<{\tfrac {c^{2}}{b^{2}}}$ und daher $p>1>q>0$ . Die größte Halbachse des Trägheitsellipsoids ist folglich verhältnismäßig kleiner, die kleinste aber verhältnismäßig größer als die entsprechende des Massenellipsoids, siehe auch Abb. 2.

Siehe auch

Euler-Kreisel

Basierend auf einem Artikel in:

Wikipedia.de