
Tangentialebene
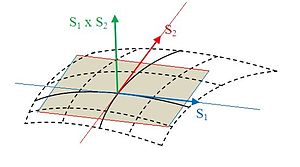
Die Tangentialebene in einem Punkt
an eine Fläche
im dreidimensionalen Raum ist diejenige Ebene, die die Fläche in der Umgebung
des Punktes
am besten annähert (berührt). Sie ist damit die zweidimensionale Entsprechung
zur Tangente einer Kurve. Wie im Fall
der Kurve existiert eine Tangentialebene nur, wenn die Fläche hinreichend
„glatt“ ist. Dies gilt zum Beispiel für die Graphen
von differenzierbaren Funktionen von zwei Variablen. Eine Fläche, die einen
Knick oder eine Spitze hat – zum Beispiel ein Kegel – besitzt in
diesen Punkten keine Tangentialebene.
Eine Ebene ist durch einen Punkt (in diesem Fall der Berührpunkt )
und zwei linear unabhängige Richtungsvektoren
oder durch einen Punkt und einen Normalenvektor
bestimmt. Je nachdem, wie eine gegebene Fläche beschrieben wird (implizit,
explizit oder parametrisiert, s.u.) wird man entweder Richtungsvektoren
oder einen Normalenvektor bestimmen.
Die Tangentialebene bildet den zweidimensionalen Spezialfall eines Tangentialraums einer Untermannigfaltigkeit
des .
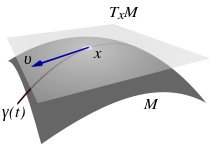
Formale Definition
Es sei
eine reguläre
Fläche und
ein Punkt.
Die Tangentialebene an
im Punkt
ist die Ebene durch
,
die von den Geschwindigkeitsvektoren von durch
verlaufenden Wegen aufgespannt wird: Ist die Funktion
ein Weg
mit
,
so ist
ein Punkt der Tangentialebene. Da die Tangentialebene zweidimensional ist,
genügen zwei solcher Wege (in verschiedene Richtungen), um die Tangentialebene
aufzuspannen.
Tangentialebene an den Graphen einer Funktion
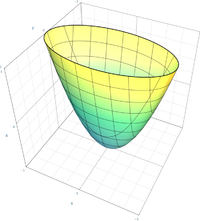
Die Fläche
ist als Graph
einer Funktion
von zwei Veränderlichen
gegeben. Gesucht ist die Tangentialebene an die Fläche in einem Punkt
.
Falls die Funktion
an der Stelle
differenzierbar
ist mit den partiellen
Ableitungen
,
liefert das Taylorpolynom
erster Ordnung
eine Gleichung der gesuchten Tangentialebene. Die Tangentialebene ist somit der Graph der affin-linearen Funktion
.
Beispiel: Die Fläche
(ein Paraboloid) ist gegeben als Graph der Funktion
mit
.
Es sei
.
Mit
und
ergibt sich
bzw.
als Gleichung der gesuchten Tangentialebene im Flächenpunkt .
Tangentialebene an eine implizit gegebene Fläche
In diesem Fall ist die Fläche als Niveaufläche
einer Funktion
von 3 Variablen gegeben. Zum Beispiel ist die Einheitskugel durch die Gleichung
gegeben. Es sei
ein Punkt der Fläche d.h. es ist
.
Falls
im Punkt
differenzierbar ist und
gilt, so wird die Tangentialebene im Punkt
durch die Gleichung
dargestellt. Begründung: Der Vektor
zeigt in die Richtung der stärksten Zunahme von
und muss damit ein Normalenvektor der gesuchten Tangentialebene sein.
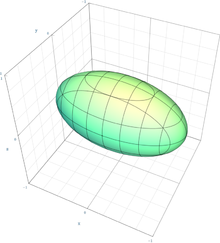
Beispiel: Die Fläche
ist ein Ellipsoid mit der Gleichung
,
gesucht ist die Tangentialebene von
im Punkt
.
Es gilt
und die gesuchte Tangentialebene hat die Koordinatengleichung
bzw.
.
Tangentialebene einer parametrisierten Fläche
.png)
In diesem Fall ist die Fläche durch eine Parameterdarstellung
gegeben. Ist die Parameterdarstellung
in einem Parameterpunkt
differenzierbar und sind die Ableitungsvektoren
linear
unabhängig, so ist
eine Parameterdarstellung der Tangentialebene im Punkt .
Beispiel:
ist eine Parameterdarstellung des Affensattels.
Mit
und
ergibt sich für die Tangentialebene in einem beliebigen Punkt
.
Bemerkung: Das Beispiel des Affensattels zeigt, dass eine Fläche
durchaus auf mehrere Möglichkeiten dargestellt werden kann: 1) parametrisiert
wie hier eingeführt, 2) als Graph der Funktion
und schließlich 3) implizit durch
.
Schnitt einer Tangentialebene mit der Fläche
Es gibt Flächen, die in der Nähe eines Punktes auf einer Seite der Tangentialebene in diesem Punkt liegen. Z.B.: Paraboloid und Ellipsoid (s.o.) oder Zylinder. Allerdings ist es auch möglich, dass die Fläche in der Nähe eines Punktes auf beiden Seiten der Tangentialebene in diesem Punkt liegt. Z.B. Affensattel oder hyperbolisches Paraboloid. Ist die Gauß-Krümmung in einem Flächenpunkt nicht Null, so gilt: bei positiver Gaußkrümmung tritt der erste Fall (Fläche auf einer Seite) und bei negativer Gaußkrümmung der zweite Fall (Fläche auf beiden Seiten) ein. Ist die Gaußkrümmung Null, so sind beide Fälle möglich. Z.B.: Zylinder überall oder Affensattel im Nullpunkt.
Anwendungen
Überall, wo die Beschreibung einer Fläche für Berechnungen zu kompliziert ist, verwendet man Tangentialebenen als Ersatz für die gegebene Fläche, z.B. bei
- der Bestimmung von Punkten der Schnittkurve zweier Flächen (Newton-Verfahren),
- der Bestimmung von Umrisspunkten einer Fläche: Die Projektionsrichtung liegt in der Tangentialebene eines Umrisspunktes,
- Abbildungen (Projektionen von Flächen auf eine Ebene, wie es etwa für Karten notwendig ist).
Literatur
- Meyberg & Vachenauer: Höhere Mathematik 1. Springer-Verlag, Berlin 1995, ISBN 3-540-59188-5, S. 380, 392, 468
- Do Carmo: Differentialgeometrie von Kurven und Flächen, Vieweg-Verlag, 1983


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 28.08. 2022