Exakte Differentialgleichung
ΦEine exakte (oder vollständige) Differentialgleichung ist eine gewöhnliche Differentialgleichung der Form
,
bei der es eine stetig
differenzierbare Funktion
gibt, so dass gilt
und
.
Eine solche Funktion
heißt dann Potentialfunktion des Vektorfelds
.
Einführung
Die Differentialgleichung
wird durch die Trennung
der Variablen gerne in der Darstellung
angegeben. Der Vorteil dieser Darstellung liegt darin begründet, dass die
linke Seite der Differentialgleichung – also
– als Bestandteil eines totalen
Differentials aufgefasst werden kann, mit
.
Hierbei übernimmt die Funktion
die Bedeutung eines Skalarpotentials
mit der Bedingung
sowie
.
Demnach muss es ein Vektorfeld
geben, welches aus dem Gradienten des Skalarpotentials gebildet werden kann,
also
.
Sind
und
stetig partiell
differenzierbar und ist der Definitionsbereich von
und
ein einfach zusammenhängendes
Gebiet
,
so gibt es genau dann ein Skalarpotential
,
wenn die sogenannte Integrabilitätsbedingung
erfüllt ist. Demzufolge muss für die zweifach stetig partiell
differenzierbare Funktion
gelten:
.
Der Sachverhalt, dass
ist, wird im Satz
von Schwarz behandelt. Zudem bedeutet die angegebene
Integrabilitätsbedingung auch, dass wenn die Rotation
des Vektorfeldes
auf einem einfach zusammenhängenden Gebiet verschwindet, also
gilt, ein Skalarpotential
existiert.
Wird andererseits die rechte Seite der Differentialgleichung
mit dem totalen
Differential der Funktion
verknüpft, so ergibt sich eine Pfaffsche
Form in der Darstellung
und nach einer beidseitigen Integration der Gleichung folgt
.
Somit wird anschaulich, dass es eine Konstante
geben muss, die für alle
die Funktion
erfüllt. Die Lösung
ist daher die Anfangsbedingung der Differentialgleichung und stellt eine Äquipotentiallinie
dar.
wird im Zusammenhang mit der exakten Differentialgleichung auch als Erstes Integral bezeichnet.
Definition
In einem einfach zusammenhängenden Gebiet
ist eine exakte Differentialgleichung gegeben durch
wenn folgende Voraussetzungen gelten:
- Die Funktionen
sind stetig partiell differenzierbar.
- Die Integrabilitätsbedingung
ist erfüllt.
- Es existiert ein zweifach stetig partiell differenzierbares
Skalarpotential
, so dass
sowie
gilt.
- Es ist ein Anfangswert
vorgegeben.
Lösungsmethode
Um die exakte Differentialgleichung zu lösen, ist es erforderlich, das Skalarpotential
wie folgt zu ermitteln :
- Integrabilitätsbedingung: Die Differentialgleichung ist exakt, wenn die Integrabilitätsbedingung
- erfüllt ist. Falls dies nicht der Fall ist, kann die Differentialgleichung eventuell mittels eines integrierenden Faktors gelöst werden.
- Erstes Integral: Wenn eine exakte Differentialgleichung vorliegt, wird mittels Integration aus der Beziehung
- das Skalarpotential zu
- bestimmt. Dabei ist
eine von
unabhängige Integrationskonstante, die jedoch bzgl.
variabel ist. Insofern ist das Skalarpotential bis auf eine unbekannte Funktion
bestimmt. Um nun die noch unbekannte Funktion
zu ermitteln, wird die Integrabilitätsbedingung in der Integraldarstellung genutzt. Durch Integration von
- erhält man
- wobei die rechte Seite der Gleichung
liefert. Nach Umformen folgt
- Durch nochmalige Integration ergibt sich
- und somit lautet eine Lösung des gesuchten Skalarpotentials
- Die Stammfunktion
wird auch als Erstes Integral der exakten Differentialgleichung bezeichnet.
- Anfangsbedingung: Bei allen zuvor durchgeführten Integrationen
blieb die Integrationskonstante unberücksichtigt, da diese aus dem Anfangswert
berechnet wird. Da neben der exakten Differentialgleichung für die Lösung ein
Anfangswert nötig ist, kann nun mit
das Skalarpotential
ermittelt werden.
-
- Ohne Anfangswert: Ist der Anfangswert
nicht bekannt, so ergibt die Differentialgleichung
die Lösung
. Diese Anfangsbedingung liefert dann, eingesetzt in das Erste Integral, die gewünschte Lösung der exakten Differentialgleichung
- Ohne Anfangswert: Ist der Anfangswert
-
- Mit Anfangswert: Ist ein Anfangswert
vorgegeben, so muss die Gleichung
erfüllt sein. Dieser Anfangswert liefert dann, eingesetzt in das Erste Integral, die gewünschte Lösung der exakten Differentialgleichung
- Mit Anfangswert: Ist ein Anfangswert
- einfach zusammenhängendes Gebiet: Schlussendlich ist zu prüfen, ob die Lösung ein einfach zusammenhängendes Gebiet abdeckt. Falls dies nicht der Fall ist, muss geprüft werden, ob durch geeignete Restriktionen die Lösung auf ein einfach zusammenhängendes Gebiet reduziert werden kann.
- Beispiel
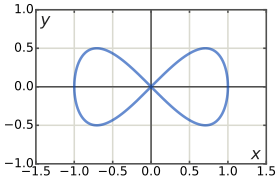
Es soll die exakte Differentialgleichung der Lemniskate von Gerono berechnet werden. Es wird also die Differentialgleichung
mit dem Anfangswert
betrachtet. Demnach ist
und die Integrabilitätsbedingung ergibt
.
Die Differentialgleichung ist also exakt und das Erste Integral kann sofort
bestimmt werden. Dazu wird zunächst
berechnet
Somit ist
und das zweite Integral verschwindet, da der Integrand nicht von
abhängig ist. Die Integrationskonstanten werden, wie zuvor ausgeführt, nicht
berücksichtigt. Unter dieser Voraussetzung lässt sich das Erste Integral
bestimmen zu
Mit
und dem Anfangswert
ergibt sich als Lösung der impliziten
Kurve
.
Integrierende Faktoren
Für eine gewöhnliche Differentialgleichung der Form ,
welche die Integrabilitätsbedingung
nicht erfüllt, lässt sich gelegentlich eine nullstellenfreie stetig
differenzierbare Funktion
derart bestimmen, dass
eine exakte Differentialgleichung wird. In diesem Fall wird
als integrierender Faktor oder eulerscher Multiplikator
bezeichnet. Da
nach Definition niemals Null wird, hat die exakte Differentialgleichung
dieselben Lösungen wie vor der Multiplikation mit
Dabei ist
genau dann ein integrierender Faktor, wenn die Integrabilitätsbedingung in der
Darstellung
erfüllt wird.
Es ist normalerweise schwierig, diese partielle Differentialgleichung
allgemein zu lösen. Da man aber nur eine spezielle Lösung
benötigt, wird man versuchen, mit speziellen Ansätzen für
eine Lösung zu finden. Solche Ansätze könnten beispielsweise lauten:
.
Integrierender Faktor  und
und 
Ein einfaches Beispiel für einen integrierenden Faktor
ist dann gegeben, wenn dieser nur von einer Variablen
oder
abhängt.
Zunächst wird der Fall betrachtet bei dem der integrierende Faktor nur von
abhängig ist und infolge dessen
ist. Unter dieser Voraussetzung ergibt die Integrabilitätsbedingung
im Zusammenhang mit der Produktregel folgende Darstellung
und nach Umformen folgt
was sich auch schreiben lässt als
Die Kettenregel für die logarithmische Ableitung liefert schließlich
Beidseitige Integration dieser Gleichung ergibt unter Auslassung der Integrationskonstanten
oder
Demnach ist der integrierende Faktor
nur von
abhängig, wenn folgender Ausdruck nur eine Funktion von
ist:
Auf die gleiche Weise lässt sich zeigen, dass der integrierende Faktor
nur von
abhängt, wenn
nur eine -Abhängigkeit
hat und der integrierende Faktor lautet dann
- Beispiel
Ausgehend von der Differentialgleichung
mit
und
wird erkennbar, dass die Integrabilitätsbedingung nicht erfüllt ist. Da
nur von
abhängt, ist es sinnvoll den integrierenden Faktor so zu wählen, dass
nur von
abhängig ist und somit
Also lautet der integrierende Faktor
Integrierender Faktor 
Hängt
von
ab, so lautet der integrierende Faktor
- Beweis
Es ist
und auf die gleiche Weise ergibt sich
Wird nun die Integrabilitätsbedingung in die Darstellung
gebracht, so folgt
Literatur
- Harro Heuser: Gewöhnliche Differentialgleichungen, Vieweg+Teubner 2009 (6. Auflage), Seite 91–102, ISBN 978-3-8348-0705-2


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 18.06. 2021