Bézierkurve
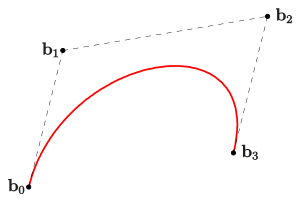
Die Bézierkurve [be'zje…] ist eine parametrisch modellierte Kurve, die ein wichtiges Werkzeug bei der Beschreibung von Freiformkurven und -flächen darstellt.
In der Computergrafik finden Bézierkurven wegen ihrer optischen Eleganz und der verhältnismäßig leichten mathematischen Handhabbarkeit häufig Anwendung. Sie werden zur Definition von Kurven und Flächen in Vektorgrafiken genutzt. Mögliche Anwendungsfälle finden sich z.B. im Computer Aided Design, bei der Erstellung von Illustrationen oder der Beschreibung von Schrifttypen (z.B. Postscript, Type1, TrueType und CFF-OpenType).
Die Bézierkurve wurde Anfang der 1960er Jahre unabhängig voneinander von Pierre Bézier bei Renault und Paul de Casteljau bei Citroën für Computer-Aided Design (computerunterstützte Konstruktion) entwickelt. Paul de Casteljau gelang zwar die Entdeckung früher, Citroën hielt seine Forschungen jedoch bis zum Ende der 1960er Jahre als Betriebsgeheimnis zurück.
Verallgemeinerungen des Konzepts der Bézierkurven führen zu den Bézierflächen.
Motivation, Definition
Numerisch einfache Kurven in der Ebene sind solche, die mit Hilfe einer
Parameterdarstellung
beschrieben werden, wobei
und
Polynome in
sind. Ist
,
und setzt man ,
so lässt sich die Kurve übersichtlicher durch
beschreiben.
Im Allgemeinen sagen die Koeffizienten-Punkte
nicht viel über den Kurvenverlauf aus. Nur
(Punkt der Kurve) und
(Tangentenvektor) haben konkrete geometrische Bedeutungen. Dies ändert sich,
wenn man die Polynome
nicht in der Monom-Basis
,
sondern in der folgenden Bernsteinbasis
darstellt:
Es sei nun
festgewählt und die Vektoren
beschreiben ein ebenes oder räumliches Polygon. Dann heißt
eine Bezierkurve
vom (maximalen) Grad .
Die Punkte
nennt man Kontrollpunkte der Bezierkurve.
Eigenschaften der Bernsteinpolynome:
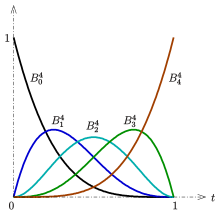
für
für
- Das Bernsteinpolynom
hat genau ein Maximum und zwar an der Stelle
D.h. eine leichte Veränderung des Punktes
hat nur eine wesentliche Veränderung der Kurve in der Umgebung von
zur Folge.
Eigenschaften einer Bézierkurve:
ist der Anfangs-,
der Endpunkt
ist die Richtung der Tangente im Punkt
ist die Richtung der Tangente im Punkt
- Das Polygon
gibt einen ungefähren Verlauf der Kurve an.
Weitere Eigenschaften der Bernsteinbasis
Für Untersuchungen von Bezierkurven sind die folgenden Eigenschaften nützlich:
- Beziehung zwischen der Bernstein- und der Monom-Basis
- (MB)
- Rekursion
- (R)
- Skalierung
- (S)
- Ableitung
- (A)
- (Man beachte, dass
ist.)
- Produkt
- (P)
Weitere Eigenschaften einer Bézierkurve
In der Literatur werden noch weitere Eigenschaften einer Bézierkurve aufgelistet:
- Die Kurve liegt innerhalb der konvexen
Hülle des Kontrollpolygons. Dies folgt daraus, dass die Bernsteinpolynome
vom Grad
eine Zerlegung der Eins sind:
- Die ersten Summanden des Taylorpolynoms bei
bzw. bei
lauten für
:
- Eine Gerade schneidet eine Bézierkurve höchstens so oft, wie sie ihr Kontrollpolygon schneidet (die Kurve ist variationsreduzierend, bzw. hat eine beschränkte Schwankung).
- Eine affine Transformation (Verschiebung, Skalierung, Rotation, Scherung) kann auf die Bézierkurve durch Transformation des Kontrollpolygons angewendet werden („affine Invarianz“).
- Liegen alle Kontrollpunkte auf einer Geraden, so wird die Bézierkurve zu einer Strecke (Vorteil gegenüber der Polynominterpolation).
- Der Einfluss eines Kontrollpunktes auf die Kurve ist global. Das heißt: Verschiebt man einen Punkt, verändert sich die gesamte Kurve. Daher verwendet man in der Praxis meist Splines, zusammengesetzte Kurven festen Grades, die stetig ineinander übergehen.
- Eine Bézierkurve kann immer in zwei Bézierkurven gleicher Ordnung geteilt werden, wobei sich die neuen Kontrollpunkte aus den alten mit Hilfe des De-Casteljau-Algorithmus ergeben (s. Abschnitt Teilung einer Bezierkurve).
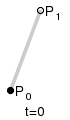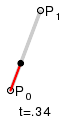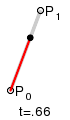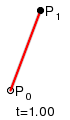
Der De-Casteljau-Algorithmus
Höhere Potenzen von
auszurechnen ist numerisch instabil. Der folgende Algorithmus führt deshalb die
Berechnung eines Kurvenpunktes auf wiederholte lineare Interpolation zurück. In
jedem Schritt wird mittels linearer Interpolation ein neues um 1 kürzeres
Polygon berechnet (s. Bild). Bei der letzten Interpolation entsteht schließlich
der Kurvenpunkt:
Für das Polygon
im
(oder
)
und einem
definiert man rekursiv für jedes
das Polygon
erzeugt. Dabei sei
.
Das Polygon der Stufe
ist identisch mit dem Ausgangspolygon, das Polygon der Stufe
ist ein Punkt, der Kurvenpunkt.
Aus der Rekursionseigenschaft (R) der Bernsteinpolynome folgt
- für
(Beweis mit Hilfe vollständiger Induktion über r.) Also ist
die Bezierkurve mit dem Kontrollpolygon .
Diese Methode, einen Punkt der Bezierkurve durch lineare Interpolationen zu
bestimmen, heißt De-Casteljau-Algorithmus.
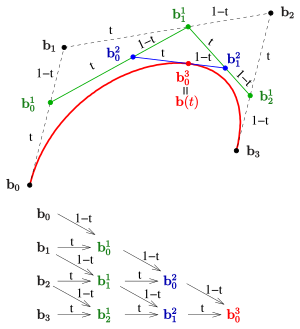
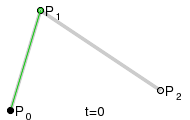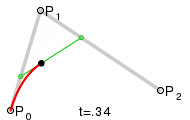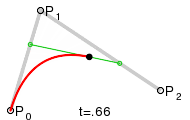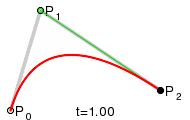
Wie für ein
mit Hilfe des Casteljau-Algorithmus aus dem Kontrollpolygon die Zwischenpolygone
und schließlich der Punkt der Bezierkurve entsteht, zeigt die Abbildung für
.
Die neuen Punkte teilen immer die alten Strecken, auf denen sie liegen, im
gleichen Verhältnis
.
Bézierkurven bis zum dritten Grad
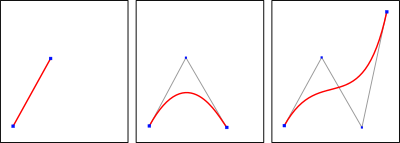
Lineare Bézierkurven (n=1):
Zwei Kontrollpunkte
und
bestimmen eine gerade Strecke zwischen diesen beiden Punkten. Der Verlauf dieser
linearen Bézier„kurve“ wird beschrieben durch
Quadratische Bézierkurven (n=2):
Eine quadratische Bézierkurve ist der Pfad, der durch die Funktion
für die Punkte
,
und
beschrieben wird:
Die letzte Zeile zeigt: Eine quadratische Bézierkurve ist eine Parabel.
Mit Hilfe des De-Casteljau-Algorithmus ausgedrückt:
Kubische Bézierkurven (n=3):
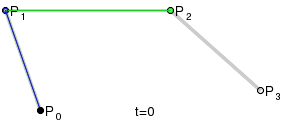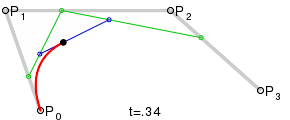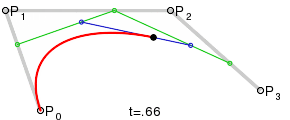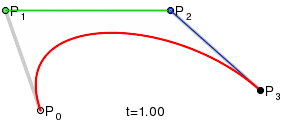
Kubische Bézierkurven sind in der Praxis von großer Bedeutung, da sowohl B-Spline-Kurven als auch NURBS stückweise in kubische Bézierkurven umgewandelt werden, um dann effizient mit dem De-Casteljau-Algorithmus gezeichnet zu werden. Selbiges gilt für hermitesche Splines, die in ihrer kubischen Form vor allem in der Computeranimation zur Interpolation zwischen Keyframes verwendet werden.
Mit Hilfe des De-Casteljau-Algorithmus ausgedrückt:
Vergleich der Kurvendarstellungen

Polynomiale Kurven (d.h. die Koordinaten sind Polynome bzgl. )
lassen sich in der Monom-Basis, der Bernsteinbasis und mit Hilfe
des De-Casteljau-Algorithmus (fortgesetzte lineare Interpolation) beschreiben.
Da die Koeffizientenpunkte der Monom-Basis nicht viel über den Kurvenverlauf
aussagen, entstanden die Darstellungen mit der Bernstein-Basis (Bezier-Kurven)
und mit dem De-Casteljau-Algorithmus. Die letzten beiden haben allerdings auch
Vor- und Nachteile. Der De-Casteljau-Algorithmus hat gegenüber der
Bezierdarstellung bei der Berechnung der Punkte (Numerik) Vorteile. Bezierkurven
lassen sich dafür durch die vielen formalen Eigenschaften (s.o.) der
Bernstein-Polynome leichter theoretisch (z.B. Krümmung) untersuchen. Der
numerische Nachteil der Bezier-Kurven (Auswertung der Bernstein-Polynome) lässt
sich durch eine dem Horner-Schema
ähnlichen Methode ausgleichen:
function bezier_comp(degree: integer; coeff : r_array; t: real) : real;
{Berechnet eine Komponente einer Bezier-Kurve. (Aus FARIN: Curves and Surfaces...)}
var i,n_choose_i : integer; fact,t1,aux : real;
begin
t1:= 1-t; fact:=1; n_choose_i:= 1;
aux:= coeff[0]*t1;
for i:= 1 to degree-1 do
begin
fact:= fact*t;
n_choose_i:= n_choose_i*(degree-i+1) div i;
aux:= (aux + fact*n_choose_i*coeff[i])*t1;
end;
aux:= aux + fact*t*coeff[degree] ;
bezier_comp:= aux;
end; {bezier_comp}
Ableitungen einer Bézier-Kurve
Mit Hilfe der Ableitungen der Bernsteinpolynome ergibt sich für die 1.
Ableitung der Bézierkurve :
Lässt man die Tangentenvektoren alle im Nullpunkt des Koordinatensystems
beginnen, so beschreiben sie eine weitere Bézierkurve mit den Kontrollpunkten
.
Speziell gilt:
und
Um höhere Ableitungen übersichtlich schreiben zu können, führt man folgenden Differenzenoperator ein:
Es ist
Die -te
Ableitung der Bézierkurve
lässt sich jetzt wie folgt schreiben:
Speziell für
und
erhält man
und
Graderhöhung einer Bézierkurve
Eine wichtige Manipulation der Darstellung einer vorgegebenen Bézierkurve ist
die sog. Graderhöhung. Sie ist vergleichbar mit dem Anfügen von Termen
an ein Polynom
.
Dabei ändert sich das Polynom nicht und der (scheinbare) Grad wird erhöht.
Analog stellt man eine fest vorgegebene Bézierkurve
in der Form
mit geeigneten neuen Kontrollpunkten
dar. Um die neuen Kontrollpunkte zu bestimmen, multipliziert man die
ursprüngliche Darstellung mit dem Faktor
:
Die neuen Kontrollpunkte sind also:
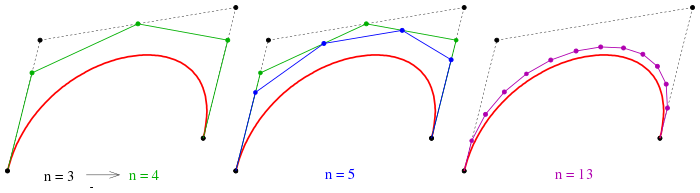
Kontrollpolygone bei ein-, zwei- und 10-maliger Graderhöhung}
Wesentliche Eigenschaften der Graderhöhung sind:
- Wiederholte Graderhöhung führt zu einer Approximation der Bézierkurve durch das Kontrollpolygon.
- Die größere Anzahl von Kontrollpunkten bietet mehr Freiheitsgrade, die Kurve zu verändern.
- Mehrere Bézierkurven lassen sich auf einen einheitlichen Grad bringen. Dies ist wichtig bei Tensorprodukt-Bézierflächen.
- Damit lassen sich auch dann quadratische Bézierkurven als kubische darstellen, falls ein Vektorzeichenprogramm (z.B. Inkscape) bzw. eine Grafikbibliothek (z.B. Cairo) nur kubische unterstützt.
Teilung einer Bézierkurve
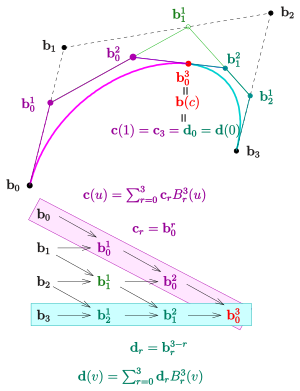
Eine Bezierkurve
ist normalerweise definiert für
.
Sei nun
.
Dann ist
mit
ein Teil der gegebenen Bézierkurve. Es soll nun die Teilkurve
als Bézierkurve
mit
vom (selben) Grad
mit geeigneten Kontrollpunkten
dargestellt werden. Setzt man
,
so muss die folgende Gleichung erfüllt sein:
für
Dies gilt für
(s. Casteljau-Alg. und Abbildung)
Denn
-
-
-
wegen
(s. Eigensch. (S) der Bernst.-Pol.)
-
-
-
Der restliche Bogen ist die Bézierkurve
mit den Kontrollpunkten
(s. Abbildung)
Rationale Bezierkurven
Rationale Kurven und projektive Kurven
Bézierkurven sind parametrisierte Kurven, deren Parameterdarstellungen nur Polynome verwenden. Leider lassen sich so wichtige und geometrisch einfache Kurven wie Kreise nicht durch polynomiale Parameterdarstellungen beschreiben. Dieser Nachteil ist u.a. das Motiv für die Erweiterung der als Parameterfunktionen zulässigen Funktionen auf rationale Funktionen. Denn jeder Kegelschnitt hat eine rationale Darstellung. Da eine Kurve mit einer rationalen Darstellung
wobei die Funktionen
und
Polynome sind, in homogenen Koordinaten die polynomiale Darstellung
besitzt, lassen sich ebene Kurven mit rationalen Koeffizientenfunktionen als
Zentralprojektion
einer Bézierkurve im
auf die Einbettungsebene
auffassen.
Die analoge Aussage gilt für Kurven im .
Sie lassen sich als Zentralprojektion einer Bézierkurve im
auf den Einbettungsraum
auffassen. Damit lassen sich die Vorteile der Bézier-Darstellung einer
polynomialen Kurve auch für rationale Kurven nutzen.
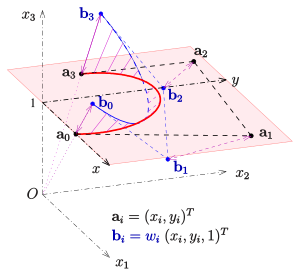
Ebene rationale Bézierkurven
Es sei nun
festgewählt und die Vektoren
beschreiben ein Polygon im
.
Dann ist
eine (räumliche) Bézier-Kurve vom Grad .
Die Punkte
sind die Kontrollpunkte der (räumlichen) Bézierkurve. Fasst man die
1-dimensionalen Unterräume
als Punkte der reellen projektiven
Ebene mit der Ferngerade
auf, so bezeichnet man den affinen Anteil (Projektion vom Nullpunkt aus auf die
Ebene
)
dieser projektiven Kurve als rationale Bézierkurve.
Die Kontrollpunkte der Bézierkurve im
lassen sich folgendermaßen beschreiben:
falls
nicht auf der Ferngerade
und
falls
auf der Ferngerade liegt.
Beim Übergang zu inhomogenen Koordinaten wird ein Kontrollpunkt entweder auf
den affinen Punkt
oder auf den Fernpunkt in Richtung
abgebildet. Der Punkt
heißt eigentlicher bzw. uneigentlicher Kontrollpunkt der
rationalen Bezierkurve und die Zahl
heißt das Gewicht des Kontrollpunktes
wobei
für eigentliche und
für uneigentliche Kontrollpunkte zu setzen ist.
Die rationalen Bezierkurven haben (u.a.) die folgenden Eigenschaften:
Sind
eigentliche Kontrollpunkte bzw. die Gewichte einer rationalen Bezierkurve
,
so gilt
- Die Kurve
enthält die Kontrollpunkte
(erster bzw. letzter Punkt des Kontrollpolygons).
- Die Tangente im Punkt
bzw.
hat die Richtung
bzw.
.
- Eine Erhöhung des Gewichts
bewirkt eine Veränderung der Kurve auf den Kontrollpunkt
zu. (s. Abbildung)
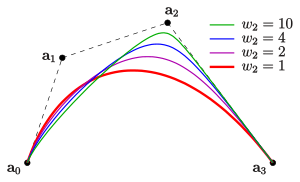
Zusammenfassung:
Eine ebene rationale Bezierkurve besitzt neben dem
Kontrollpolygon noch die Gewichte
als Designparameter. Will man eine Kurve erzeugen, legt man zunächst die
Kontrollpunkte
und die Gewichte
fest. Dadurch wird dann auch eine räumliche (gewöhnliche) Bezierkurve mit den
Kontrollpunkten
definiert. Die Projektion dieser Kurve (vom Nullpunkt aus) auf die x-y-Ebene
(
)
liefert dann die ebene rationale Bezierkurve. Eine Variation der Gewichte ändert
nicht die Kontrollpunkte
,
aber die (räumlichen) Kontrollpunkte
und damit die zugehörige räumliche Bezierkurve und schließlich auch die (ebene)
rationale Bézierkurve. Erhöht man ein Gewicht
,
so entfernt sich der zugehörige Kontrollpunkt
vom Nullpunkt und zieht die räumliche Bezierkurve mit. Der zugehörige
Kontrollpunkt
dagegen bleibt unverändert. Die rationale Bezierkurve bewegt sich auf ihn zu (s.
Bild). Verringert man das Gewicht, bewegt sich die Kurve von dem Kontrollpunkt
weg. Falls alle Gewichte 1 sind, ist die rationale Bézierkurve eine gewöhnliche
Bézierkurve mit den Kontrollpunkten
.
Kegelschnitte als rationale Bézierkurven
Parabel:
Eine Bézierkurve vom Grad zwei mit nicht kollinearen
Kontrollpunkten
im
ist immer eine Parabel (s. oben). Um eine Parabel als (ganz-)rationale
Bezierkurve darzustellen, wählt man drei nicht kollineare Kontrollpunkte
und setzt
und
.
Letzteres bedeutet: Die Kontrollpunkte sind alle eigentlich.
Ellipsen und Hyperbeln lassen sich durch Zentralprojektion von Parabeln im
,
deren Ebenen nicht den Nullpunkt enthalten, auf die Einbettungsebene
erzeugen.
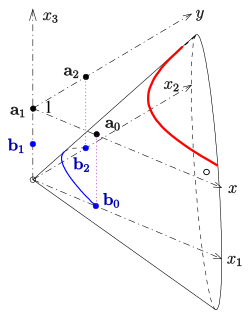
Hyperbel:
Für die Kontrollpunkte
beschreibt
eine Parabel, die auf dem Kegel mit der Gleichung
liegt (s. Bild). Die Kontrollpunkte und Gewichte der zugehörigen (ebenen)
rationalen Bezierkurve sind:
bzw. :
.
sind uneigentliche Kontrollpunkte. Damit ist
und der Nenner (s.o.) der rationalen Komponenten ist
.
Also ist die zugehörige rationale Bézierkurve
Dies ist eine rationale Parameterdarstellung eines Astes der Hyperbel mit der
Gleichung .
Die Änderung
liefert eine rationale Bézierdarstellung der Hyperbel
.
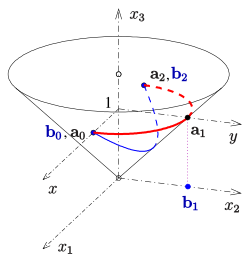
Kreis:
In dem folgenden Beispiel sind die Kontrollpunkte der
(räumlichen) Parabel:
.
Die Bézierkurve
liegt in diesem Fall auf dem Kegel mit der Gleichung
(s. Abbildung). Die Kontrollpunkte und Gewichte der zu gehörigen rationalen
Bezierkurve sind:
bzw.
.
ist uneigentlicher Kontrollpunkt. Damit ist
und der Nenner (s.o.) der rationalen Komponenten ist
.
Also ist die zugehörige rationale Bezierkurve
Für
ist dies eine rationale Parameterdarstellung eines halben Einheitskreises.
Setzt man
erhält man eine rationale Bézierdarstellung der Ellipse mit der Gleichung
.
Anwendung: Kreisapproximation durch kubische Bézierkurven
Kreise bzw.
Kreisbögen lassen sich durch
Bézierkurven nicht exakt, sondern nur genähert darstellen. Eine solche Näherung
ist z.B. für die Gestaltung einer Typ-1-PostScript-Schrift
nötig, da hier nur Strecken und Bézierkurven dritten Grades erlaubt sind.
(Jedoch verläuft auch für größere
keine Bézierkurve
-ten
Grades in einem noch so kleinen Kreisbogen mit Radius
zum Mittelpunkt
,
denn
liegt genau dann auf dem Kreisbogen, wenn
Nullstelle der Polynomfunktion
vom Grad
ist, was höchstens
Male vorkommt.)
Teilt man einen Kreis in nur zwei (gleich große) Segmente und nähert die Halbkreise durch kubische Bézierkurven, zeigen sich größere Abweichung von der Kreisgestalt. Durch eine feinere Unterteilung in mehr Segmente lässt sich ein Kreis besser nähern. Je geringer der überstrichene Winkelbereich des Kreissegments ist, desto genauer ist die Näherung durch die Bézierkurve. Eine oft verwendete, einfache Realisierung eines Kreises verwendet vier Viertelkreisbögen, die als kubische Bézierkurven dargestellt werden. Um die Verbesserung der Näherung durch Verfeinerung der Unterteilung zu demonstrieren, werden in der Folge die Fehler der Halbkreisapproximation und der Viertelkreisapproximation miteinander verglichen.
Notation: Wir untersuchen Approximationen eines Kreises
mit folgenden Parametern:
ist der Radius von
ist der Mittelpunkt von
- die Kontrollpunkte
und
liegen vom Mittelpunkt
im Abstand
entfernt (also auf der Kreislinie von
)
ist eine reelle Zahl zwischen 0 und 1 (
entspräche einer quadratischen Bézierapproximation).
Die zusätzlichen Kontrollpunkte
und
werden so gewählt, dass
zu
und
zu
den Abstand
hat.
Beispielkoordinaten Viertelkreis:
Als einfaches Beispiel einer Viertelkreisapproximation wählen wir:
- den Mittelpunkt
des Kreises
als
,
- den Kontrollpunkt
auf der Kreislinie als
,
- den Kontrollpunkt
auf der Kreislinie als
– die Strecke
steht also senkrecht auf
, so dass beide Strecken einen Viertelkreissektor bilden –,
- den Kontrollpunkt
als
(auf der Strecke
),
- den Kontrollpunkt
als
(auf der Strecke
).
Die vier Kontrollpunkte liegen also auf dem Rand des Quadrats mit den
Eckpunkten ,
,
und
.
Dies gewährleistet immerhin, dass die Näherungskurve und die Kreislinie in
und
dieselbe Tangente haben. So ist auch
die aus den Viertelkreisapproximationen zusammengesetzte Kurve in den
Knotenpunkten „glatt“.
Die kubische Bézierkurve
(
)
hat mit diesen Kontrollpunkten folgende Form:
Eine recht gute Approximation des oberen rechten Viertelkreisbogens erhält
man mit ,
wie die nachfolgende Betrachtung zeigt.
Fehleranalyse:
Die Abweichung der gerade angegebenen Bézierkurve
vom darzustellenden Kreis
lässt sich folgendermaßen quantifizieren:
Ein Punkt
der Bézierkurve
liegt genau dann auf der vorgegebenen Kreislinie mit Radius
um den Mittelpunkt
,
wenn
(„Koordinatengleichung“)
gilt. Definiert man
so ist das äquivalent zu .
ist ein Maß für die Abweichung der Approximation
von der Kreisgestalt.
Fordert man dann die Übereinstimmung der Bézierkurve
mit dem Kreis
bei der Winkelhalbierenden, erhält man
Der Fehler ist Null bei ,
sonst überall positiv, d.h. die Bézierkurve liegt stets auf oder außerhalb
des Kreisbogens. Der maximale Fehler beträgt
bei
und bei
.
Fordert man, dass die aufsummierten Fehler über die gesamte Kurve
verschwinden (
kann sowohl positiv als auch negativ sein – die Bézierkurve verläuft teils
außerhalb, teils innerhalb der Kreislinie – und das Integral darüber kann Null
ergeben), erhält man
Die größten Abweichungen liegen bei etwa
und bei
.
Beide Approximationen sind somit für viele Anwendungsbereiche ausreichend.
Beispielkoordinaten Halbkreis:
Bei einer Halbkreisnäherung mit ,
,
,
und
,
mit
beträgt die maximale Abweichung
.
Dies ist bzgl. der maximalen Abweichung etwa 50 mal schlechter als die
Viertelkreisapproximation.
Literatur
- Gerald Farin: Curves and Surfaces for CAGD. A practical guide. 5. Auflage. Academic Press, San Diego 2002, ISBN 1-55860-737-4
- J. Hoschek, D. Lasser: Grundlagen der geometrischen Datenverarbeitung. Vieweg+Teubner Verlag, 1989, ISBN 978-3-519-02962-5
- Boaswan Dzung Wong: Bézierkurven: gezeichnet und gerechnet. Orell Füssli Verlag, Zürich 2003, ISBN 3-280-04021-3


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 19.04. 2023