Steifes Anfangswertproblem

Ein steifes Anfangswertproblem ist in der Numerik gewöhnlicher Differentialgleichungen ein Anfangswertproblem

$y'(t)=f(t,y(t)),\ t\geq t_{0},\quad y(t_{0})=y_{0}$

bei dem explizite Einschrittverfahren oder Mehrschrittverfahren wegen ihres beschränkten Stabilitätsgebiets erhebliche Schwierigkeiten haben. Dies ist dann der Fall, wenn die Konstante in der Lipschitzbedingung (vgl. Satz von Picard-Lindelöf)

$\|f(t,y_{1})-f(t,y_{2})\|\leq L\|y_{1}-y_{2}\|$

große Werte $L\gg 1$ annimmt, die Lösung y(t) aber recht glatt verläuft. In diesem Fall könnten numerische Verfahren diese Lösung mit relativ großen Schrittweiten genau approximieren, explizite Verfahren werden aber wegen des beschränkten Stabilitätsgebiets gezwungen, kleine Schrittweiten zu verwenden. Typischerweise treten steife Anfangswertprobleme bei der numerischen Approximation von parabolischen partiellen Differentialgleichungen auf nach erfolgter Diskretisierung im Ortsbereich. Ein Beispiel ist das Crank-Nicolson-Verfahren, bei dem im Ort eine Finite-Differenzen-Methode und in Zeitrichtung die implizite Trapez-Methode eingesetzt wird.

Beispiel

Die Problematik wird mit dem expliziten und impliziten Eulerverfahren und Schrittweite h>0 anhand des linearen Anfangswertproblems

$y'(t)=\lambda {\big (}y(t)-2{\big )},\quad y(0)=1,$

mit $\lambda =-4$ erläutert. Die exakte Lösung ist $y(t)=2-e^{{-4t}}$ und für große ist die Lösung beinahe konstant, also sehr glatt.

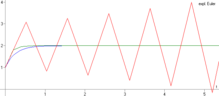
Explizites Euler-Verfahren im Beispiel

Das explizite Eulerverfahren berechnet mit $y_{0}=1$ die Näherungen

$y_{k+1}=(1+h\lambda )y_{k}-2h\lambda ,\ k=1,2,3,\ldots .$ Diese liefern aber nur dann brauchbare Werte, wenn der Betrag des Vorfaktors von $y_{k}$ kleiner eins ist, $|1+h\lambda |<1$ , hier also für h<1/2

. Für

liegt dagegen das Produkt $h\lambda =-4h$ außerhalb des Stabilitätsgebiets, das bei endet, siehe Eulersches Polygonzugverfahren. Für solche, zu großen Schrittweiten wachsen die Lösungen unbegrenzt an, vgl. Grafik.

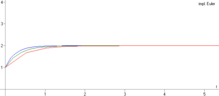
Implizites Euler-Verfahren im Beispiel

Das implizite Eulerverfahren berechnet dagegen von $y_{0}=1$ ausgehend die Näherungen

$y_{k+1}={\frac {y_{k}-2h\lambda }{1-h\lambda }},\ k=1,2,3,\ldots .$ Für jede positive Schrittweite ist hier der Vorfaktor von $y_{k}$ , der Bruch $1/(1-h\lambda )<1$ , da $\lambda =-4$ negativ ist. Denn das Stabilitätsgebiet des impliziten Eulerverfahrens umfasst die ganze linke komplexe Halbebene, das Verfahren ist A-stabil.

Die beiden Diagramme zeigen jeweils die exakte Lösung in blau, eine Näherungslösung mit kleiner Schrittweite $h=0{,}2$ in grün und die Näherungslösungen mit $h=0{,}52$ in rot.

Beim expliziten Eulerverfahren wachsen die roten Näherungen immer weiter an, während auch diese groben Näherungen beim impliziten Eulerverfahren in der Nähe der exakten Lösung bleiben.

Erweiterte Stabilitätsbegriffe

Für eine genauere Klassifikation numerischer Verfahren bei steifen Anfangswertproblemen wurden in der Literatur verschiedene Stabilitätsbegriffe eingeführt, die sich in der Regel an unterschiedlichen Testgleichungen orientieren. Dazu gehören die

Gleichung von Dahlquist $y'(t)=\lambda y(t)$ mit $\operatorname {Re} (\lambda )<0$ . Ihre Lösungen $y(t)=e^{{\lambda (t-t_{0})}}y_{0}$ gehen alle gegen null für $t\to \infty$ .
Prothero-Robinson-Gleichung $y'(t)=\lambda {\big (}y(t)-g(t){\big )}+g'(t)$ mit $\operatorname {Re} (\lambda )<0$ und einer glatten Funktion . Die Lösung dieser Gleichung ist $y(t)=g(t)+e^{{\lambda (t-t_{0})}}(y_{0}-g(t_{0}))$ . Für sehr kleine Realteile $\operatorname {Re} (\lambda )\ll -1$ nähern sich alle Lösungen sehr schnell der Funktion an.
Die nichtlineare dissipative Gleichung $y'(t)=f{\big (}t,y(t){\big )}$ , bei der die rechte Seite eine einseitige Lipschitzbedingung erfüllt, $(y-v)^{T}{\big (}f(t,y)-f(t,v){\big )}\leq \mu \|y-v\|_{2}^{2},\quad y,v\in \mathbb{R} ^{n}.$ Im Unterschied zur obigen Lipschitzbedingung sind bei der Konstanten $\mu$ auch negative Werte möglich. Eine Folge der einseitigen Lipschitzbedingung ist, dass für die Differenz von zwei Lösungen der Differentialgleichung die Schranke $\|y(t)-v(t)\|_{2}\leq e^{{\mu (t-t_{0})}}\|y(t_{0})-v(t_{0})\|_{2}$ gilt, und sich diese für $\mu<0$ und wachsendes $t\to \infty$ also immer weiter annähern.

Bei numerischen Verfahren ist es vorteilhaft, wenn sich die numerischen Approximationen bei Testgleichungen im Wesentlichen so wie die exakten Lösungen verhalten. Dementsprechend fordert der Begriff

A-Stabilität, dass Näherungslösungen bei der ersten Testgleichungen gegen Null gehen für $t\to \infty$ ,
B-Stabilität, dass sich zwei Näherungslösungen der dritten Testgleichung mit $\mu =0$ nicht voneinander entfernen für $t\to \infty$ .

Für implizite Runge-Kutta-Verfahren gibt es mit dem Begriff Algebraische Stabilität ein hinreichendes Kriterium für B-Stabilität.

Numerische Verfahren für steife Anfangswertprobleme

Für steife Anfangswertprobleme sind implizite Verfahren effizienter als explizite (das kann man quasi auch als Definition des Begriffs "steif" ansehen). Spezielle Klassen sind

implizite Runge-Kutta-Verfahren
Rosenbrock-Wanner-Verfahren
BDF-Verfahren

Da bei impliziten Verfahren die Auflösung der nichtlinearen Gleichungssysteme einen hohen Aufwand erfordert, wurden auch linear-implizite Einschrittverfahren entwickelt wie die genannten Rosenbrock-Wanner-Verfahren (ROW-Methoden).

Basierend auf einem Artikel in:

Wikipedia.de