Gauß-Quadratur
Die Gauß-Quadratur (nach Carl
Friedrich Gauß) ist ein Verfahren zur numerischen
Integration, das bei gegebenen Freiheitsgraden eine optimale Approximation
des Integrals liefert. Bei diesem Verfahren wird die zu integrierende Funktion
aufgeteilt in
,
wobei
eine Gewichtsfunktion ist und
durch ein spezielles Polynom
mit speziell gewählten Auswertungspunkten
approximiert wird. Dieses Polynom lässt sich exakt integrieren. Das Verfahren
ist also von der Form
.
Die Gewichtsfunktion
ist größer gleich Null, hat endlich viele Nullstellen und ist integrierbar.
ist eine stetige Funktion. Der
Integrationsbereich
ist nicht auf endliche Intervalle beschränkt. Weiterhin werden
als Knoten, Abszissenwerte oder Stützstellen und die Größen
als Gewichte bezeichnet.
Das Verfahren wurde 1814 von Gauß veröffentlicht, in der heutigen Form mit orthogonalen Polynomen von Carl Gustav Jacobi 1826.
Eigenschaften
Um optimale Genauigkeit zu erreichen, müssen die Abszissenwerte
einer Gauß-Quadraturformel vom Grad
genau den Nullstellen des
-ten
orthogonalen
Polynoms
vom Grad
entsprechen. Die Polynome
,
,
…,
müssen dabei orthogonal bezüglich des mit
gewichteten Skalarprodukts
sein,
Für die Gewichte gilt:
Die Gauß-Quadratur stimmt für polynomiale Funktionen ,
deren Grad maximal
ist, mit dem Wert des Integrals exakt überein. Es lässt sich zeigen, dass keine
Quadraturformel existiert, die alle Polynome vom Grad
exakt integriert. In dieser Hinsicht ist die Ordnung des Quadraturverfahrens
optimal.
Ist die zu integrierende Funktion
hinreichend glatt, d.h. ist sie
mal stetig
differenzierbar in
,
so kann für den Fehler
der Gaußquadratur mit
Stützstellen gezeigt werden:
für ein
.
Anwendung
Die gaußsche Quadratur findet Anwendung bei der numerischen Integration.
Dabei werden für eine gegebene Gewichtsfunktion und einen gegebenen Grad n, der
die Genauigkeit der numerischen Integration bestimmt, einmalig die Stützpunkte
und Gewichtswerte
berechnet und tabelliert. Anschließend kann für beliebige
die numerische Integration durch einfaches Aufsummieren von gewichteten
Funktionswerten erfolgen.
Dieses Verfahren ist damit potentiell vorteilhaft
- wenn viele Integrationen mit derselben Gewichtsfunktion durchgeführt werden müssen und
- wenn
hinreichend gut durch ein Polynom approximierbar ist.
Für einige spezielle Gewichtsfunktionen sind die Werte für die Stützstellen und Gewichte fertig tabelliert.
Gauß-Legendre-Integration
Dies ist die bekannteste Form der Gauß-Integration auf dem Intervall ,
sie wird oft auch einfach als Gauß-Integration bezeichnet. Es gilt
.
Die resultierenden orthogonalen Polynome sind die Legendre-Polynome
erster Art. Wir erhalten mit den Stützpunkten
und den zugehörige Gewichten
die Approximation
.
Die Erweiterung auf beliebige Intervalle
erfolgt durch eine Variablentransformation:
.
Die Stützpunkte (auch Gaußpunkte genannt) und Gewichte der Gauß-Legendre-Integration sind:
| n=1 | ||
| 1 | 0 | 2 |
| n=2 | ||
| 1 | 1 | |
| 2 | 1 | |
| n=3 | ||
| 1 | ||
| 2 | 0 | |
| 3 | ||
| n=4 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| n=5 | ||
| 1 | ||
| 2 | ||
| 3 | 0 | |
| 4 | ||
| 5 |
Gauß-Tschebyschow-Integration
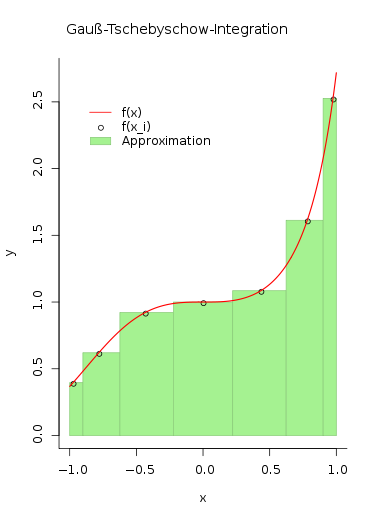
Eine Variante der Gauß-Integration auf dem Intervall
ist jene mit der Gewichtsfunktion
.
Die dazugehörigen orthogonalen Polynome sind die Tschebyschow-Polynome,
deren Nullstellen und damit auch die Stützpunkte der Quadraturformel direkt in
analytischer Form vorliegen:
während die Gewichte nur von der Anzahl der Stützpunkte abhängen:
.
Die Erweiterung auf beliebige Intervalle
erfolgt durch eine Variablentransformation (siehe unten). Das gesuchte Integral
kann umgeformt werden in
.
Zur numerischen Berechnung wird das Integral nun durch die Summe
approximiert. Durch Einsetzen der Stützpunkte in analytischer Form erhält man
,
was der n-fachen Anwendung der Mittelpunktsregel über dem Intervall 0 bis Pi entspricht. Der Fehler kann für einen geeigneten Wert für t zwischen 0 und Pi abgeschätzt werden über
Gauß-Hermite-Integration
Gauß-Integration auf dem Intervall .
Es gilt
.
Die resultierenden orthogonalen Polynome sind die Hermite-Polynome. Das
gesuchte Integral
kann umgeformt werden in
.
Zur numerischen Berechnung wird es nun durch die Summe
approximiert.
Stützpunkte und Gewichte der Gauß-Hermite-Integration:
| n=1 | |||
| 1 | 0 | 1,7724538509055159 | |
| n=2 | |||
| 1 | 1,46114118266 | ||
| 2 | 1,46114118266 | ||
| n=3 | |||
| 1 | 1,32393117521 | ||
| 2 | 0 | 1,1816359006 | |
| 3 | 1,32393117521 | ||
| n=4 | |||
| 1 | −1,65068012389 | 0,0813128354472 | 1,2402258177 |
| 2 | −0,524647623275 | 0,804914090006 | 1,05996448289 |
| 3 | 0,524647623275 | 0,804914090006 | 1,05996448289 |
| 4 | 1,65068012389 | 0,0813128354472 | 1,2402258177 |
Gauß-Laguerre-Integration
Gauß-Integration auf dem Intervall .
Es gilt
.
Die resultierenden orthogonalen Polynome sind die Laguerre-Polynome.
Das gesuchte Integral
kann umgeformt werden in
.
Zur numerischen Berechnung wird es nun durch die Summe
approximiert.
Stützpunkte und Gewichte der Gauß-Laguerre-Integration:
| n=1 | |||
| 1 | 1 | 1 | 2,7182818284590451 |
| n=2 | |||
| 1 | 1,53332603312 | ||
| 2 | 4,45095733505 | ||
| n=3 | |||
| 1 | 0,415774556783 | 0,711093009929 | 1,07769285927 |
| 2 | 2,29428036028 | 0,278517733569 | 2,7621429619 |
| 3 | 6,28994508294 | 0,0103892565016 | 5,60109462543 |
| n=4 | |||
| 1 | 0,322547689619 | 0,603154104342 | 0,832739123838 |
| 2 | 1,74576110116 | 0,357418692438 | 2,04810243845 |
| 3 | 4,53662029692 | 0,038887908515 | 3,63114630582 |
| 4 | 9,3950709123 | 0,000539294705561 | 6,48714508441 |
Gauß-Lobatto-Integration
Mit dieser nach Rehuel Lobatto benannten Version wird auf dem Intervall
integriert, wobei zwei der
Stützstellen an den Enden des Intervalls liegen. Die Gewichtsfunktion ist
.
Polynome
bis zum Grad
werden exakt integriert.
Dabei ist ,
und
bis
sind die Nullstellen der ersten Ableitung des Legendre-Polynoms
.
Die Gewichte sind
| n | Stützstellen |
Gewichte |
|---|---|---|
Variablentransformation bei der Gauß-Quadratur
Ein Integral über
wird auf ein Integral über
zurückgeführt, bevor man die Methode der Gauß-Quadratur anwendet. Dieser
Übergang kann durch
mit
und
sowie
und Anwendung der Integration
durch Substitution mit
auf folgende Weise geschehen:
Seien nun
die Stützstellen und
die Gewichte der Gauß-Quadratur über dem Intervall
,
bzw.
.
Deren Zusammenhang ist also durch
gegeben.
Adaptives Gauß-Verfahren
Da der Fehler bei der Gauß-Quadratur, wie oben erwähnt, abhängig von der
Anzahl der gewählten Stützstellen ist und sich mit einer größeren Anzahl
Stützstellen gerade der Nenner erheblich vergrößern kann, legt dies nahe,
bessere Näherungen mit größerem
zu erhalten. Die Idee ist, zu einer vorhandenen Näherung
eine bessere Näherung, beispielsweise
,
zu berechnen, um die Differenz zwischen beiden Näherungen zu betrachten. Sofern
der geschätzte Fehler
eine gewisse absolute Vorgabe
überschreitet, ist das Intervall aufzuteilen, sodass auf
und
die
-Quadratur
erfolgen kann. Jedoch ist die Auswertung einer
Gauß-Quadratur ziemlich kostspielig, da insbesondere für
im Allgemeinen
neue Stützstellen berechnet werden müssen, sodass sich für die Gauß-Quadratur
mit Legendre-Polynomen die adaptive Gauß-Kronrod-Quadratur anbietet.
Adaptive Gauß-Kronrod-Quadratur
Die präsentierte Kronrod-Modifikation, welche nur für die
Gauß-Legendre-Quadratur existiert, basiert auf der Verwendung der bereits
gewählten
Stützstellen und der Hinzunahme von
neuen Stützstellen.
Während die Existenz optimaler Erweiterungen für die Gauß-Formeln von Szegö
belegt wurde, leitete Kronrod (1965) für die Gauß-Legendre-Formeln optimale
Punkte her, die den Präzisionsgrad
sicherstellen.
Wenn die mithilfe der erweiterten Knotenzahl von
berechnete Näherung als
definiert wird, lautet die Fehlerschätzung:
Diese kann dann mit einem
verglichen werden, um dem Algorithmus ein Abbruchkriterium zu geben. Die
Kronrod-Knoten und -Gewichte zu den
Gauß-Legendre-Knoten und -Gewichten sind für
in der folgenden Tabelle festgehalten. Die Gauß-Knoten wurden mit einem (G)
markiert.
| n=3 | ||
| 1 | ~0,960491268708020283423507092629080 | ~0,104656226026467265193823857192073 |
| 2 | ~0,774596669241483377035853079956480 (G) | ~0,268488089868333440728569280666710 |
| 3 | ~0,434243749346802558002071502844628 | ~0,401397414775962222905051818618432 |
| 4 | 0 (G) | ~0,450916538658474142345110087045571 |
| 5 | ~-0,434243749346802558002071502844628 | ~0,401397414775962222905051818618432 |
| 6 | ~-0,774596669241483377035853079956480 (G) | ~0,268488089868333440728569280666710 |
| 7 | ~-0,960491268708020283423507092629080 | ~0,104656226026467265193823857192073 |
| n=7 | ||
| 1 | ~0,991455371120812639206854697526329 | ~0,022935322010529224963732008058970 |
| 2 | ~0,949107912342758524526189684047851 (G) | ~0,063092092629978553290700663189204 |
| 3 | ~0,864864423359769072789712788640926 | ~0,104790010322250183839876322541518 |
| 4 | ~0,741531185599394439863864773280788 (G) | ~0,140653259715525918745189590510238 |
| 5 | ~0,586087235467691130294144838258730 | ~0,169004726639267902826583426598550 |
| 6 | ~0,405845151377397166906606412076961 (G) | ~0,190350578064785409913256402421014 |
| 7 | ~0,207784955007898467600689403773245 | ~0,204432940075298892414161999234649 |
| 8 | 0 (G) | ~0,209482141084727828012999174891714 |
| 9 | ~-0,207784955007898467600689403773245 | ~0,204432940075298892414161999234649 |
| 10 | ~-0,405845151377397166906606412076961 (G) | ~0,190350578064785409913256402421014 |
| 11 | ~-0,586087235467691130294144838258730 | ~0,169004726639267902826583426598550 |
| 12 | ~-0,741531185599394439863864773280788 (G) | ~0,140653259715525918745189590510238 |
| 13 | ~-0,864864423359769072789712788640926 | ~0,104790010322250183839876322541518 |
| 14 | ~-0,949107912342758524526189684047851 (G) | ~0,063092092629978553290700663189204 |
| 15 | ~-0,991455371120812639206854697526329 | ~0,022935322010529224963732008058970 |


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 26.02. 2021