Laguerre-Polynome
Laguerre-Polynome (benannt nach Edmond
Laguerre) sind spezielle Polynome,
die auf dem Intervall
ein orthogonales
Funktionensystem bilden. Sie sind die Lösungen der laguerreschen
Differentialgleichung. Eine wichtige Rolle spielen die Laguerre-Polynome in
der theoretischen
Physik, insbesondere in der Quantenmechanik.
Differentialgleichung und Polynome
Laguerresche Differentialgleichung
Die laguerresche Differentialgleichung
,
ist eine gewöhnliche lineare Differentialgleichung zweiter Ordnung für
und
Sie ist ein Spezialfall der Sturm-Liouville-Differentialgleichung
Erste Polynome
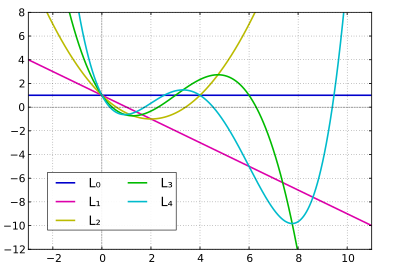
Die ersten fünf Laguerre-Polynome lauten
In der Physik wird üblicherweise eine Definition verwendet, nach der die
Laguerre-Polynome um einen Faktor
größer sind.
Eigenschaften
Rekursionsformeln
Das Laguerre-Polynom
lässt sich mit den ersten beiden Polynomen
über die folgende Rekursionsformel berechnen
Des Weiteren gelten folgende Rekursionsformeln:
,
,
.
Eine explizite Formel für die Laguerre-Polynome lautet
.
- Beispiel
Es wird das Polynom
für
berechnet. Also
.
Um dieses Polynom zu erhalten, ist es notwendig, das Polynom
für
zu bestimmen. Es ergibt sich
Somit lautet das Polynom
Rodrigues-Formel
Das -te
Laguerre-Polynom lässt sich mit der Rodrigues-Formel
wie folgt darstellen
und
Aus der ersten Gleichung berechnet sich das Laguerre-Polynom mit der Produktregel
für höhere Ableitungen und den Identitäten ,
sowie
gemäß
Aus der zweiten Gleichung ergibt sich das Laguerre-Polynom mit dem binomischen
Lehrsatz und der Identität
wie folgt
Orthogonale Polynome
Da die Laguerre-Polynome für
und/oder
divergent sind, bilden sie keinen Prähilbertraum
und keinen Hilbertraum.
Deshalb wird eine Gewichtsfunktion eingeführt welche die Lösung der
Differentialgleichung ungeändert lässt und welche dafür sorgt, dass die
Laguerre-Polynome quadratintegrierbar
werden. Unter diesen Voraussetzungen bilden die Eigenfunktionen
eine Orthonormalbasis
im Hilbertraum
der quadratintegrierbaren Funktionen mit der Gewichtsfunktion
.
Demzufolge gilt
Hierbei bedeutet
das Kronecker-Delta.
- Beweis
Teil 1: Zunächst wird gezeigt, dass die Laguerre-Polynome mit dem
Gewicht
orthogonal sind, für
gilt demnach
Mit dem Sturm-Liouville-Operator
ergeben sich für die Laguerre-Polynome
folgende Ausgangsgleichungen:
- (1)
und
- (2)
.
Wird Gleichung (1) von links mit
multipliziert und von Gleichung (2), welche ebenfalls von links mit
multipliziert wird, subtrahiert, so ergeben sich die beiden Gleichungen:
- (3)
und
- (4)
.
Zunächst wird Gleichung (3) zusammengefasst. Mit der Produktregel
für Ableitungen, der Term
bleibt hierbei unberücksichtigt, ergeben sich folgende Darstellungen
und
.
Auf diese Weise wird erkennbar, dass der zweite Term in beiden Ableitungen gleich ist und bei der Differenzenbildung verschwindet, also:
- (5)
wobei
die Wronski-Determinante
der Funktionen
bedeutet.
Zur Berechnung der Wronski-Determinante mittels der Abelschen
Identität wird die Differentialgleichung
oder
betrachtet, so dass eine hebbare
Singularität bei
entsteht. Die Koeffizientenmatrix des Fundamentalsystems
lautet dann
und deren Spur
ist
.
Somit lautet die Abelsche Identität:
.
Da
und
linear unabhängig sind, ist
– bei genauer Betrachtung ist
– und es ergibt sich folgendes Resultat:
Die Integrationskonstante wird
gewählt und Gleichung (5) wird mit
multipliziert, so dass folgt:
Nach Umformen und Trennung der Variablen lautet die Gleichung nun:
Auf beiden Seiten der Gleichung stehen nun eindimensionale Pfaffsche Formen und da
eine konstante Funktion ist, gilt
.
Für die Berechnung der verbleibenden Pfaffschen Form ist eine geeignete
Parametrisierung
zu wählen. Das Integral lautet nun:
.[1]
Demnach verschwindet das Integral längs dem Intervall ,
so dass unter Verwendung von Gleichung (4) gilt:
Diese Bedingung kann nur erfüllt werden, wenn:
.
Teil 2: Im Folgenden wird gezeigt, dass die Laguerre-Polynome mit
dem Gewicht
beschränkt
sind,[2]
für
gilt demnach
,
oder abkürzend
.
Für den Beweis wird einerseits die Reihendarstellung
und anderseits die Rodrigues-Formel
benutzt. Es gilt:
.
Für
mit
ergibt sich:
.
Wird nun für
das Laguerre-Polynom zerlegt, so folgt:
Durch diese Zerlegung wird der Grad des Polynoms in der Summe um 1 reduziert
und in der Folge gilt ,
wie in Teil 1 gezeigt. Es verbleibt somit lediglich der zweite Term, der
mit partieller
Integration berechnet wird, also:
Die Stammfunktion wurde mithilfe der Produktregel berechnet und es ergibt
sich im Grenzwert .
Dasselbe Resultat wird im Grenzwert
erhalten. Da dieses Ergebnis für alle
partiellen Integrationen gilt, folgt:
Mittels weiterer -facher
partieller Integration oder Integrationstabelle folgt
und somit:
.
Aus Teil 1 und Teil 2 ergibt sich:
Erzeugende Funktion
Eine erzeugende Funktion für das Laguerre-Polynom lautet
Zugeordnete Laguerre-Polynome
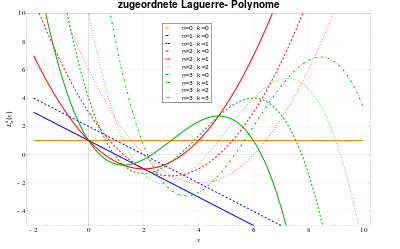
Die zugeordneten (verallgemeinerten) Laguerre-Polynome hängen mit den gewöhnlichen Laguerre-Polynomen über
zusammen. Ihre Rodrigues-Formel lautet
Die zugeordneten Laguerre-Polynome erfüllen die zugeordnete Laguerre-Gleichung
Die ersten zugeordneten Laguerre-Polynome lauten:
Zur Berechnung lässt sich die Rekursionsformel
verwenden.
Der Sturm-Liouville-Operator lautet
und mit der Gewichtsfunktion
gilt:
Zugeordnete Laguerre-Polynome lassen sich als Wegintegrale ausdrücken:
Dabei ist
ein Weg, der den Ursprung einmal im Gegenuhrzeigersinn umrundet und die
wesentliche Singularität bei 1 nicht einschließt.
Wasserstoffatom
Die Laguerre-Polynome haben eine Anwendung in der Quantenmechanik bei der Lösung der Schrödinger-Gleichung für das Wasserstoffatom bzw. im allgemeinen Fall für ein Coulomb-Potential. Mittels der zugeordneten Laguerre-Polynome lässt sich der Radialanteil der Wellenfunktion schreiben als
(Normierungskonstante ,
charakteristische Länge
,
Hauptquantenzahl
,
Bahndrehimpulsquantenzahl
).
Die zugeordneten Laguerre-Polynome haben hier also eine entscheidende Rolle. Die
normierte Gesamtwellenfunktion ist durch
gegeben, mit der Hauptquantenzahl
,
der Bahndrehimpulsquantenzahl
,
der magnetischen Quantenzahl
,
dem bohrschen
Radius
und der Kernladungszahl
.
Die Funktionen
sind die zugeordneten Laguerre-Polynome,
die Kugelflächenfunktionen.
Anmerkungen
- ↑
Wegen der linearen Parametrisierung kann o.B.d.A.
das Differential
gewählt werden.
- ↑ In der Physik wird statt beschränkt üblicherweise der Begriff normiert verwendet.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 25.03. 2021