Bohrscher Radius

Physikalische Konstante
Name	Bohrscher Radius
Formelzeichen	$\,a_0$
Größenart	Länge
Wert
SI	5.291 772 109 03(80) • 10^-11 m
Unsicherheit (rel.)	1.5 • 10^-10
Gauß	5.291 772 109 03(80) • 10^-9 cm
Bezug zu anderen Konstanten
$a_0 = {{4\pi\varepsilon_0\hbar^2}\over{m_{\mathrm{e}} e^2}}$
Quellen und Anmerkungen
Quelle SI-Wert: CODATA 2018

Der bohrsche Radius $\,a_0$ bezeichnet den Radius des Wasserstoffatoms im niedrigsten Energiezustand und somit auch den Radius seiner ersten und kleinsten Elektronenschale im Rahmen des bohrschen Atommodells; dabei bleibt die kleine Korrektur, die der Mitbewegung des Atomkerns um den Schwerpunkt entspricht, noch unberücksichtigt.

Eine quantenmechanische Betrachtung ergibt, dass im niedrigsten Energiezustand die radiale Wahrscheinlichkeitsdichte, das Elektron zu messen, beim bohrschen Radius maximal wird. Der experimentell relevantere Erwartungswert für den Radius ist jedoch das 1,5-fache des bohrschen Radius.

Formeln und Zahlenwert

Der bohrsche Radius errechnet sich gemäß der Formel:

$a_0 = {{4\pi\varepsilon_0\hbar^2}\over{m_{\mathrm{e}} e^2}}\,.$

Dabei ist

$\,\varepsilon_0$ die elektrische Feldkonstante im Vakuum,
$\,\hbar$ die durch $2\pi$ geteilte Plancksche Konstante,
$\,m_{\mathrm{e}}$ die Masse des Elektrons und
$\,e$ die Ladung des Elektrons.

Ebenso wird der bohrsche Radius beschrieben durch

$a_0 = \frac{\lambda_{\mathrm{e}}}{2 \pi \alpha}$

mit

der Compton-Wellenlänge $\lambda_{\mathrm{e}} = \frac{2 \pi \hbar}{m_{\mathrm{e}} c}$ des Elektrons und
der Feinstrukturkonstante $\alpha = \frac{e^2}{4 \pi \varepsilon_0 \hbar c}.$

Der Wert beträgt nach derzeitiger Messgenauigkeit der in die Rechnung einfließenden Naturkonstanten:

$a_{0}=0{,}529\,177\,210\,903(80)\cdot 10^{-10}\,\mathrm {m} ,$

wobei die eingeklammerten Ziffern die geschätzte Standardabweichung von 0,000 000 000 080 · 10⁻¹⁰ m angeben.

Mit dieser Definition gilt der bohrsche Radius als eine Naturkonstante. Zum Beispiel in der Atomphysik wird sie oft als Längeneinheit benutzt, wobei als Näherungen 52,9 pm oder ein halbes Ångström (= 50 pm) verwendet werden.

Berücksichtigt man die endliche Masse $M_\mathrm{K}$ des Kerns und damit seine Mitbewegung um den gemeinsamen Schwerpunkt, muss man in den mechanischen Formeln die Elektronenmasse $m_{\mathrm {e} }$ durch die reduzierte Masse $\mu = \tfrac{m_\mathrm{e}}{(1+\frac{m_\mathrm{e}}{M_\mathrm{K}})}$ ersetzen. Der Bahnradius wird dann $\left(1+\tfrac{m_\mathrm{e}}{M_\mathrm{K}}\right) a_0$ . Die Korrektur beträgt beim H-Atom nur ca. 0,05 %, beim He⁺-Ion, das ebenfalls nur ein Elektron besitzt, ca. 0,01 %. Mit entsprechenden Werten für die Masse wird der Begriff des bohrschen Radius auch für andere Systeme verwendet, z.B. Exzitonen.

Herleitung

Siehe auch: „Bohrsches Atommodell“ für eine vollständige Herleitung.

Schon mithilfe einer einfachen Abschätzung und unter Berücksichtigung der Unschärferelation lässt sich der bohrsche Radius ermitteln.

Es wird angenommen, dass der Abstand des im Wasserstoffatom gebundenen Elektrons zum Kern für gewöhnlich beträgt.

Der Unschärferelation wegen lässt sich der Impuls des Elektrons grob mit

$p=\hbar / a$

angeben, wobei die Ortsobservable hier durch den Abstand ersetzt wird.

Die kinetische Energie beträgt demnach

$E_\mathrm{kin}(a) = \frac 12 m_\mathrm{e} v^2 = \frac 12 \frac{p^2}{m_\mathrm{e}} = \frac 12 \frac{1}{m_\mathrm{e}} \left( \frac{\hbar}{a} \right)^2. \!\,$

Die potentielle Energie ist gemäß dem Coulombschen Gesetz

$V(a)=-\frac{1}{4 \pi \varepsilon_0} \frac{e^2}{a}, \!\,$

woraus sich die Gesamtenergie ergibt:

$E(a)=E_\mathrm{kin}(a)+V(a)=\frac{\hbar^2}{2m_\mathrm{e}a^2}-\frac{1}{4 \pi \varepsilon_0} \frac{e^2}{a} \!\, .$

Je weiter sich das Elektron vom Kern entfernt, desto kleiner wird seine kinetische Energie. Wegen des negativen Vorzeichens wächst damit aber seine potentielle Energie.

Kinetische, potentielle und gesamte Energie des Elektrons in Abhängigkeit vom Abstand (in bohrschen Radien) des Elektrons vom Atomkern für das Wasserstoffatom im Grundzustand

Im Grundzustand realisiert sich eine Art „Kompromiss“, der die Gesamtenergie minimal macht; der zugehörige Radius ergibt sich, indem man die Energie nach differenziert und die Ableitung gleich null setzt (Extremwertermittlung):

$\frac{\mathrm{d}E}{\mathrm{d}a} = 0 \Rightarrow a_0 = \frac{4 \pi \hbar^2 \varepsilon_0}{m_\mathrm{e} e^2}.$

Dies ist genau der bohrsche Radius.

Setzt man nun $a_{0}$ in E(a) ein, so erhält man die Rydberg-Energie, die Ionisierungsenergie des Wasserstoffs:

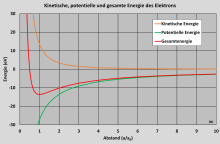
$E(a_0) = - \frac{1}{2} \frac{m_\mathrm{e} \, e^4}{(4 \pi)^2 \, \varepsilon_0^2 \, \hbar^2} = - \frac{1}{2} \frac{e^2}{4 \pi \, \varepsilon_0 \, a_0} = -13{,}6 \, \mathrm{eV}.$

Die Abbildung zeigt den Verlauf von kinetischer, potentieller und Gesamtenergie in Abhängigkeit vom Abstand (in bohrschen Radien). Setzt man $a_{0}$ in die Formel für $E_{\mathrm {kin} }(a)$ bzw. V(a) ein, so ergeben sich

$E_{\mathrm {kin} }(a_{0})=-E(a_{0})$

bzw.

$V(a_{0})=2\cdot E(a_{0})$ .

Der Betrag der potentiellen Energie $|V(a_{0})|$ wird als Hartree-Energie bezeichnet und ist eine weitere Einheit des Systems atomarer Einheiten der Atomphysik.

Historisches

Niels Bohr erwähnt in seinem Aufsatz den österreichischen Physiker Arthur Erich Haas, der die Formel für $\,a_0$ schon 1910/11 gefunden und damit erstmals die Rolle erkannt hatte, die die Plancksche Konstante $\,h$ in der Atomphysik, insbesondere in ihren mechanischen Aspekten, spielen könnte. In seinem Modell läuft ein Elektron auf der Oberfläche einer mit $\,1 e$ positiv geladenen Kugel um, was nach dem Gaußschen Gesetz der Elektrostatik dieselbe Anziehungskraft ergibt wie ein punktförmiger Kern. Dieses Modell fand damals keine Beachtung, u.a. weil man vielfach auch beim Wasserstoff noch von einer viel größeren Anzahl von Elektronen ausging, also entsprechend auch von einer größeren positiven Ladung des Rests des insgesamt neutralen Atoms. Auch hielt man es weithin für ausgeschlossen, dass $\,h$ außerhalb des Themas harmonische Schwingungen eine Bedeutung haben könnte.

Anfangs lagen die mit dem bohrschen Radius $a_{0}$ berechneten Energien bzw. Wellenlängen des Wasserstoffspektrums um 0,05 % neben den damals bekannten Messwerten, beim Helium-Ion um 0,01 %. Doch dass die kleinen Korrekturen wegen der Mitbewegung des Kerns in beiden Fällen volle Übereinstimmung erbrachten, sicherte dem bohrschen Modell rasch große Anerkennung.

Literatur

R. P. Feynman: Vorlesungen über Physik. Quantenmechanik. Oldenbourg Wissenschaftsverlag, München 2007, ISBN 978-3-486-58109-6.
L. M. Brown, A. Pais, Sir B. Pippard (Hrsg.): Twentieth Century Physics. Band 1, Inst. of Phys. Publishing, Bristol 1995, ISBN 0-7503-0353-0.
Max Jammer: The Conceptual Development of Quantum Mechanics. MCGraw-Hill, New York 1966.

Basierend auf einem Artikel in:

Wikipedia.de