Aufenthaltswahrscheinlichkeit

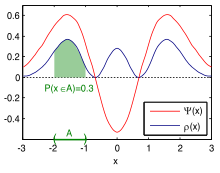
Wellenfunktion (in rot), Wahrscheinlichkeitsdichte (blau) und Aufenthaltswahrscheinlichkeit (grün) des zweiten angeregten Zustandes (n=2) eines eindimensionalen harmonischen Oszillators.
Die Wahrscheinlichkeit, ein Teilchen im Intervall A (grüner Bereich: -2< x< -1) zu finden, ist ungefähr 30 Prozent.

Die Aufenthaltswahrscheinlichkeit kennzeichnet in der Quantenphysik die Wahrscheinlichkeit, mit der ein Teilchen in einem bestimmten Bereich des (Orts-) Raumes anzutreffen ist. Sie wird durch Integration der Wahrscheinlichkeitsdichte $\rho ({\vec {r}})$ über diesen Bereich bestimmt:

$P({\vec {r}}\in A)=\int _{A}\rho ({\vec {r}})\,{{\rm {d^{3}}}}{\vec {r}}$

Nach der Kopenhagener Deutung der Quantenmechanik errechnet sich die Wahrscheinlichkeitsdichte als Betragsquadrat aus der Wellenfunktion $\Psi :$

$\rho ({\vec {r}})=|\Psi ({\vec {r}})|^{2}=\Psi ^{*}({\vec {r}})\cdot \Psi ({\vec {r}})$

mit der komplex konjugierten Wellenfunktion $\Psi ^{*}$ .

Integriert man die Wahrscheinlichkeitsdichte in Kugelkoordinaten über die Winkel und nicht zusätzlich über den Radius, so erhält man (unter Berücksichtigung der Jacobi-Determinante) die radiale Wahrscheinlichkeitsdichtefunktion.

Im Gegensatz zur Wellenfunktion selbst ist die Wahrscheinlichkeitsdichte der Beobachtung zugänglich.

Das Orbitalmodell des Atombaus stützt sich maßgeblich auf Aufenthaltswahrscheinlichkeiten: die Positionen der Elektronen (in diesem Fall als Quantenobjekte anzusehen) sind unbestimmt; es gibt lediglich Bereiche, in denen die Wahrscheinlichkeit größer ist, dort ein Elektron anzutreffen; dies sind die Orbitale.

Basierend auf einem Artikel in:

Wikipedia.de