Harmonischer Oszillator (Quantenmechanik)

Der harmonische Oszillator in der Quantenmechanik beschreibt analog zum harmonischen Oszillator in der klassischen Physik das Verhalten eines Teilchens in einem Potential der Form

$V(x)=\frac 1 2 k x^2 = \frac 1 2 m \omega^2 x^2$ .

Ein solches quadratisches Potential bezeichnet man auch als harmonisches Potential. Klassisch erhält man dieses Potential für ein System, dessen Rückstellkraft proportional zur Auslenkung aus der Ruhelage ist.

Da ein beliebiges Potential in der Nachbarschaft einer stabilen Gleichgewichtslage näherungsweise als harmonisches Potential beschrieben werden kann, ist dies eines der wichtigsten Modellsysteme in der Quantenmechanik. Zudem ist es eines der wenigen quantenmechanischen Systeme, für die eine genaue analytische Lösung bekannt ist.

Hamilton-Operator und Eigenzustände im eindimensionalen Fall

Der Hamilton-Operator, der in der Quantenmechanik die Gesamtenergie (kinetische Energie + potentielle Energie) beschreibt, ist für den harmonischen Oszillator

$\hat H = \frac{\hat{p}^2}{2 m} + \frac{m \omega^2 \hat{x}^2}{2} = -\frac{\hbar^2}{2 m}\Delta + \frac{m \omega^2 \hat x ^2}{2} .$

Dabei ist die Teilchenmasse und $\omega$ die Eigenkreisfrequenz des Oszillators. In der Ortsdarstellung ist der Ortsoperator $\hat x = x$ und der Impulsoperator $\hat p = -\mathrm i\hbar\nabla$ . Die quadrierte Ortsableitung ist durch den Laplace-Operator $\nabla^2 = \Delta$ ausgedrückt.

Die stationäre Schrödinger-Gleichung

$\hat H \psi_n(x)=E_n\psi_n(x)$

lautet damit für den eindimensionalen harmonischen Oszillator

$- \frac{\hbar^2}{2 m}\Delta \psi_n(x) + \frac{1}{2}m \omega^2 x^2\psi_n(x)=E_n\psi_n(x).$

Orts-Wellenfunktionen eines Teilchens im harmonischen Potential in den Zuständen n=0…7

Zu den Orts-Wellenfunktionen gehörende Aufenthaltswahrscheinlichkeit.

Die Eigenfunktionen $\psi_n(x)$ des harmonischen Oszillators ergeben sich durch Lösen dieser linearen Differentialgleichung. Es sind die Hermite-Funktionen

$\psi_n(x)= \left(\frac{m\omega}{\pi\hbar}\right)^\frac{1}{4}\frac{1}{\sqrt{2^nn!}} H_n\left(\sqrt{\frac{m\omega}{\hbar}} x \right) e^{-\frac{1}{2}\frac{m\omega}{\hbar}x^2}$ .

Dabei sind H_n(x) die Hermite-Polynome:

$H_n(x)=(-1)^n e^{x^2}\frac{\mathrm d^n}{\mathrm dx^n}\left(e^{-x^2}\right)$

also

$\begin{align} H_0(x)&=1\\ H_1(x)&=2x\\ H_2(x)&= (2x)^2 - 2 = 4x^2-2\\ H_3(x)&= (2x)^3 - 6 (2x) = 8x^3-12x\\ H_4(x)&= (2x)^4 - 12 (2x)^2 + 12 = 16x^4-48x^2+12\\ \ldots \end{align}$

Der Term $e^{-\frac{1}{2}\frac{m\omega}{\hbar}x^2}$ beschreibt den exponentiellen Abfall außerhalb des Oszillatorpotentials.

Der Grundzustand n=0 hat die Form einer Gauß-Kurve

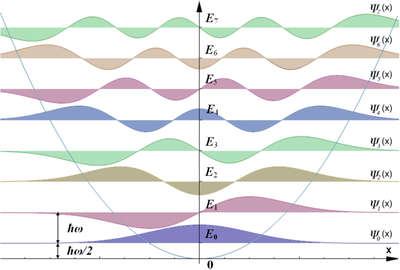
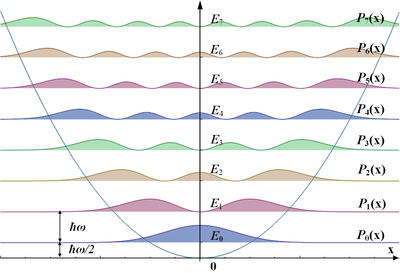
$\psi_0(x)=\left(\frac{m\omega}{\pi\hbar}\right)^\frac{1}{4} e^{-\frac{1}{2}\frac{m\omega}{\hbar}x^2}$ .

Die nebenstehende obere Grafik zeigt die ersten acht Lösungen $\psi_n(x)$ . Neben den Wellenfunktionen ist darunter auch deren Betragsquadrat dargestellt, welches die Aufenthaltswahrscheinlichkeit eines Teilchens im gegebenen harmonischen Potential angibt (jeweils blaue Parabel in den Diagrammen rechts).

Die korrespondierenden Energieniveaus ergeben sich als

$E_n=\hbar\omega\left( n+\frac{1}{2}\right)$

mit ganzzahlig positiv oder null.

Nullpunktenergie

Vergleich zwischen klassischem und quantenmechanischem Oszillator

→ Hauptartikel: Nullpunktenergie

Der Zustand mit der niedrigsten Energie liegt somit $E_0=\frac{1}{2}\hbar\omega$ über dem Potentialminimum. Dadurch ist das Teilchen in Übereinstimmung mit der heisenbergschen Unschärferelation nicht exakt bei x=0, p=0 lokalisiert, wie man es von einem klassischen Oszillator erwarten würde. Man spricht hier von einer Nullpunktenergie bzw. Nullpunktsschwingung. In den Quantenfeldtheorien führt dies zu Vakuumfluktuationen.

Die Leiteroperatormethode

Das Problem des harmonischen Oszillators in der Quantenmechanik lässt sich mittels Erzeugungs- und Vernichtungsoperatoren behandeln. Die Methode wurde von Paul Dirac, basierend auf Arbeiten von Niels Bohr und Otto Wiener, entwickelt. Dieser Lösungsweg wird auch algebraische Methode genannt.

Für diesen Lösungsweg definiert man zwei Operatoren $\hat a$ und $\hat a^\dagger$ , die einem Oszillator jeweils ein Energiequant $\hbar\omega$ entziehen oder hinzufügen. Man nennt sie deswegen Vernichtungs- und Erzeugungsoperator. Andere gebräuchliche Bezeichnungen sind Leiteroperator und Aufsteige-/Absteigeoperator. Die Notation $\psi_n(x)$ wird hierfür in die einfachere Schreibweise $\left|n\right\rangle$ (siehe auch Bra-Ket-Notation) überführt. Ein solcher Zustand heißt Fock-Zustand oder Besetzungszahlzustand, weil er die Anzahl der Energiequanten im Oszillator angibt. Man definiert diese Operatoren so, dass sie folgende Beziehungen erfüllen:

$\begin{align}\hat a\left|n\right\rangle&:=\sqrt{n}\,\left|n-1\right\rangle\\ \hat a^\dagger\left|n\right\rangle&:=\sqrt{n+1}\,\left|n+1\right\rangle \end{align}$

Die Anwendung von $\hat a$ führt somit von einem Eigenzustand $\left|n\right\rangle$ in den Eigenzustand $\left|n-1\right\rangle$ mit niedrigerem Energieniveau, die Anwendung von $\hat a^\dagger$ transformiert in die umgekehrte Richtung. Aus diesen Operatoren lässt sich noch der Besetzungszahloperator $\hat n=\hat a^\dagger\hat a$ zusammensetzen, der die Anzahl der Energiequanten in einem Zustand (also die Zahl ) liefert:

$\hat n\left|n\right\rangle=n\left|n\right\rangle$

Nun lässt sich der Hamilton-Operator mit diesen neuen Operatoren umschreiben, zu:

$\hat H=\hbar\omega\left(\hat a^\dagger\hat a+\frac{1}{2}\right) =\hbar\omega\left(\hat n+\frac{1}{2}\right)$

Die Operatoren $\hat a$ und $\hat a^\dagger$ lassen sich durch die kanonischen Operatoren $\hat x$ und $\hat p$ darstellen:

Vernichtungsoperator: $\hat a = \sqrt{\frac{m {\omega}}{2 \hbar}} \left(\hat x+\frac{\mathrm i \hat p}{m{\omega}}\right)$
Erzeugungsoperator: $\hat a^{\dagger}= \sqrt{\frac{m {\omega}}{2 \hbar}} \left(\hat x-\frac{\mathrm i\hat p}{m \omega}\right)$

Daraus folgt direkt die Darstellung von $\hat x$ sowie $\hat p$ :

$\hat x = \sqrt{\frac{\hbar}{2m\omega}}\left(\hat a^{\dagger} + \hat a\right)$

$\hat p = \mathrm i\sqrt{\frac{m \omega\hbar}{2}}\left(\hat a^{\dagger} - \hat a\right).$

Zur Bestimmung der Eigenfunktionen lässt sich die Schrödingergleichung für den niedrigsten Zustand $\left|0\right\rangle$ explizit lösen (dies ist eine einfache Differentialgleichung) und erhält so dessen Ortsdarstellung. Alle weiteren Zustände erhält man dann über die rekursive Anwendung des Erzeugungsoperators auf diesen Grundzustand:

$\left|n\right\rangle=\frac{1}{\sqrt{n!}}\left(\hat a^\dagger\right)^n\left|0\right\rangle$

Auf die gleiche Art lassen sich quantenmechanisch Teilchen bzw. Felder beschreiben. Stellt man sich etwa elektromagnetische Strahlung aus Photonen zusammengesetzt vor, so lassen sich für Photonen ebenfalls Erzeugungs- und Vernichtungsoperatoren aufstellen. Es zeigt sich, dass das elektromagnetische Feld als Ansammlung von harmonischen Oszillatoren beschrieben werden kann. Dabei steht jeder Oszillator für eine Lichtwelle bestimmter Frequenz $\omega$ . Dabei gibt die Anzahl der Photonen in dieser „Mode“ des Lichtfeldes an. Allgemein nennt man ein solches Vorgehen zweite Quantisierung Eine detaillierte Berechnung der Eigenwerte des (eindimensionalen) Oszillators ist im Artikel Erzeugungs- und Vernichtungsoperator unter bosonische Kletteroperatoren zu finden.

Klassischer Grenzfall

Im Grenzfall großer Quantenzahlen geht die Aufenthaltswahrscheinlichkeit in die klassische Aufenthaltswahrscheinlichkeit über. Diese klassische Wahrscheinlichkeitsdichte ist proportional zur inversen Geschwindigkeit 1/v . Je kleiner die Geschwindigkeit des klassischen Teilchens im Potential ist, desto länger verweilt es an einem entsprechenden Ort. Die Geschwindigkeit kann man direkt aus dem Energiesatz ableiten. Die folgende Abbildung zeigt die klassische und die quantenmechanische Aufenthaltswahrscheinlichkeitsdichte. Je größer wird, desto ähnlicher werden sich die Kurven:

Vergleich zwischen der Aufenthaltswahrscheinlichkeit eines QM-Oszillators (blau) bei n = 70 und der eines klassischen Oszillators (lila).

Quasiklassische Zustände

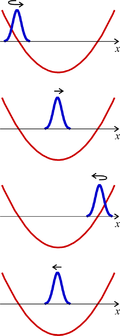
Zeitentwicklung eines quasiklassischen Zustandes im harmonischen Potential

Bringt man ein lokalisiertes Wellenpaket in ein harmonisches Potential (siehe Abbildung rechts), so verhält es sich wie ein klassisches Teilchen in diesem Potential (daher quasiklassischer Zustand). Trifft es auf die Potentialränder, so wird es umdrehen und zurücklaufen. Effektiv führt es dann eine Schwingung im Potential aus.

Mathematisch entsprechen diese Zustände kohärenten Zuständen. Sie werden durch eine komplexe Zahl $\alpha$ charakterisiert und lassen sich als Linearkombination der Zustände $\left|n\right\rangle$ darstellen:

$\left|\alpha\right\rangle=e^{-{|\alpha|^2\over2}}\sum_{n=0}^{\infty}{\alpha^n\over\sqrt{n!}}\left|n\right\rangle$

Wichtig sind solche Zustände bei der Beschreibung von kohärenter Strahlung, da man zeigen kann, dass sich das Lichtfeld in der Quantenfeldtheorie auf harmonische Oszillatoren (einer für jede Mode des Feldes) zurückführen lässt (siehe auch kohärente Strahlung). Die Wahrscheinlichkeitsverteilung der Besetzungszahlen kohärenter Zustände folgt (wie die Photonenstatistik von kohärentem Licht) der Poisson-Verteilung:

$P(n)= \left|\left\langle n|\alpha \right\rangle\right|^2 = \frac{|\alpha|^{2n}}{n!}e^{-|\alpha|^2}$

Ein dem quasiklassischen Zustand ähnlicher Zustand wird erzeugt, wenn man ein zweiatomiges Molekül (z.B. Wasserstoff H₂) mit Hilfe von intensiven Femtosekundenlasern anregt. Oben wurde bereits erläutert, dass man für die Schwingung zweiatomiger Moleküle den harmonischen Oszillator als Näherung verwenden kann. In der folgenden Abbildung ist das Geschehen gezeigt:

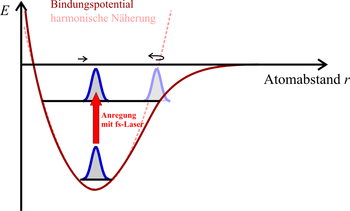
Zunächst wird mit einem Laserpuls eine tiefliegende schmale Wellenfunktion in einen höheren Energiezustand angehoben. Dort bleibt sie weiter lokalisiert und beginnt sich als „quasiklassischer Zustand“ im Potential zu bewegen. Zur Messung wird dann ein zweiter Puls eingestrahlt, der das Molekül ionisiert. Die Position der Wellenfunktion gibt den Abstand der Atome im Molekül an. Aus der kinetischen Energie der Bruchstücke kann auf diesen Abstand und die Form des Wellenpakets geschlossen werden.

N-dimensionaler harmonischer Oszillator

Der eindimensionale harmonische Oszillator kann leicht auf den N-dimensionalen Fall erweitert werden. Der Hamilton-Operator in N Dimensionen ist

$\hat H = \left( {\hat p^2 \over 2m} + {1\over 2} m \omega^2 \hat r^2 \right) = \sum_{i=1}^N \left( {\hat p_i^2 \over 2m} + {1\over 2} m \omega^2 \hat x_i^2 \right)$ .

Daraus wird deutlich, dass der N-dimensionale harmonische Oszillator genau N unabhängigen eindimensionalen harmonischen Oszillatoren mit der gleichen Masse und Rückstellkraft entspricht, denn eine Summe aus N unabhängigen Eigenfunktionen für jede Koordinate nach dem obigen eindimensionalen Schema löst die Schrödingergleichung. Dies ist eine vorteilhafte Eigenschaft des $r^2 = x_1^2 + x_2^2 + \dots + x_N^2$ Potentials (vgl. Satz des Pythagoras), welches es ermöglicht die potentielle Energie in Terme zu trennen, die nur von jeweils einer Koordinate abhängen.

Die möglichen Energieniveaus ergeben sich entsprechend zu

$E_n = \hbar \omega \left[(n_1 + \cdots + n_N) + {N\over 2}\right]= \hbar \omega \left[n + {N\over 2}\right]$ .

Zu beachten ist jedoch, dass die Energieniveaus E_n des N-dimensionalen Oszillators entsprechend der kombinatorischen Möglichkeiten zur Realisierung der Niveaus g_n -fach entartet sind wie folgt:

$g_n = \binom{N+n-1}{n}$

Gekoppelte harmonische Oszillatoren

Betrachtet man im einfachsten Fall ein System aus zwei eindimensionalen Teilchen, welche nur durch eine harmonische Kraft F=-k(x_2-x_1) aneinandergekoppelt sind, so ergibt sich dafür der Hamilton-Operator

$H = \frac{p_1^2 + p_2^2}{2m} + \frac{1}{2} \, k (x_2 - x_1)^2.$

Da (x_2 - x_1)^2 = x_1^2 + x_2^2 - 2 x_1 x_2 eine einfache Separation der Schrödingergleichung zunächst verhindert, bietet sich eine Transformation in Schwerpunkt-Koordinaten x_1', x_2' an:

$\begin{align}x_1' :=& x_1+x_2 &\qquad x_2' :=& x_2-x_1\\ x_1 =& \frac{x_1'-x_2'}{2} &\qquad x_2 =& \frac{x_1'+x_2'}{2} \end{align}$

Die Impulse lassen sich durch die Impulse der Schwerpunktkoordinaten ausdrücken als

$p_1^2+p_2^2 = \frac{p_1'^2 + p_2'^2}{2}$ .

Damit gelingt die Separation des Hamiltonoperators

$H = \frac{p_1'^2 + p_2'^2}{4m} + \frac{1}{2} k x_2'^2.$

Dies entspricht einem einzelnen harmonischen Oszillator bzgl. der Differenzschwingung x_2', p_2' der 2 Teilchen (mit doppelter reduzierter Masse), wobei sich das System als Ganzes (x_1',p_1') zusätzlich wie ein freies Teilchen bewegt. Die Lösung der Schrödingergleichung führt entsprechend zu den harmonischen Energieniveaus

$E_n = \hbar \omega_{2m} \left(n + \frac{1}{2}\right) + E_\text{translation}$ .

Bei einer Kette aus N derart paarweise harmonisch hintereinander gekoppelter Teilchen (eindimensionales Gitter) findet man ähnlich eine Koordinatentransformation $\vec x'=M\vec x$ derart, dass N-1 voneinander unabhängige kollektive harmonische Schwingungen (plus eine kommunale Schwerpunktsbewegung) resultieren.

Bei dreidimensionalen Kristallgittern in der Festkörperphysik führt diese Betrachtung dann zu den Phononen.

Anwendungen

Der harmonische Oszillator ist ein wichtiges Modellsystem der Quantenphysik, da es eines der wenigen geschlossen (also ohne Näherungen und numerische Methoden) lösbaren Systeme der Quantenmechanik ist. Mit ihm können eine Reihe physikalischer Sachverhalte näherungsweise beschrieben werden:

In der Molekülphysik erlaubt er eine Näherung der Bindungsverhältnisse zwischen Atomen und ermöglicht so z.B. eine Vorhersage über Schwingungsspektren. Dies lässt sich verdeutlichen, indem eine Bindung durch zwei über eine Feder (harmonisches Potential) miteinander verbundene Massepunkte (die Atome), die gegeneinander schwingen, dargestellt wird:

Die lineare Rückstellkraft F(x)

einer solchen Feder führt auf ein harmonisches Potential V(x)

(proportional x^2

) und somit auf den harmonischen Oszillator. In realen Molekülen sieht das Potential etwas anders aus (Morse-Potential), aber der harmonische Oszillator ist, zumindest für niedrige Schwingungsenergien, eine gute Näherung.

Ein weiteres Beispiel ist die Torsionsschwingung des Ethenmoleküls, die in der folgenden Zeichnung dargestellt ist:

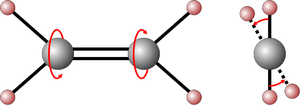
Dabei verdrillt sich sozusagen die Doppelbindung und jeweils zwei Wasserstoff-Atome schwingen drehend gegeneinander.

In der modernen Atomphysik werden zu untersuchende Atome und Ionen in optischen Fallen bzw. Ionenfallen gefangen und gekühlt, um z.B. bei Messungen eine höhere Auflösung zu erhalten. Außerdem kann man in solchen Fallen neue Zustände der Materie untersuchen (z.B. Bose-Einstein-Kondensate, Fermi-Kondensate). Solche Fallen weisen ein, in erster Näherung, parabolisches Potential auf. Somit können Teilchen in diesen Fallen ebenfalls mit dem Modell des quantenmechanischen harmonischen Oszillators beschrieben werden.
In der Festkörperphysik beschreibt das Einstein-Modell (nach Albert Einstein) eine Methode, um den Beitrag der Gitterschwingungen (Phononen) zur Wärmekapazität eines kristallinen Festkörpers zu berechnen. Grundlage ist die Beschreibung des Festkörpers als aus N quantenharmonischen Oszillatoren bestehend, die jeweils in drei Richtungen unabhängig schwingen können. Außerdem können Phononen auch durch eine Ansammlung gekoppelter harmonischer Oszillatoren beschrieben werden. Dabei ist jedes Atom im Kristallgitter ein Oszillator, der an seine Nachbaratome gekoppelt ist.

Basierend auf einem Artikel in Wikipedia.de