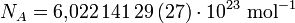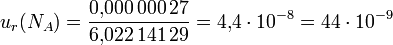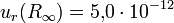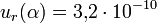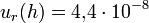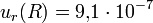Committee on Data for Science and Technology
Das Committee on Data for Science and Technology (CODATA) ist eine in Paris ansässige Organisation mit dem Ziel der Verbesserung von Qualität, Zuverlässigkeit und Zugänglichkeit von interessanten Daten aus allen Feldern der Wissenschaft und Technologie. CODATA wurde 1966 vom Internationalen Wissenschaftsrat (International Council for Science) gegründet.
CODATA-Empfehlungen für physikalische Konstanten
1969 wurde die CODATA Task Group on Fundamental Constants gegründet. Das Sekretariat der Arbeitsgruppe wird im Fundamental Constants Data Center des National Institute of Standards and Technology (NIST) geführt. Ihr Ziel ist die periodische Publikation eines optimal geschätzten Satzes von Werten physikalischer Konstantenund der zugehörigen Standardunsicherheiten. Die Optimierung erfolgt im Grundsatz nach der Methode der kleinsten Quadrate auf Basis der bis zum Stichtag verfügbaren international ermittelten relevanten Messwerte, die zur Berücksichtigung ihrer unterschiedlichen Genauigkeiten mit dem Kehrwert der Quadrate ihrer jeweiligen Standardunsicherheiten gewichtet werden. Seit 1998 werden diese Empfehlungen alle vier Jahre mit Stichtag 31. Dezember ermittelt, bei Bedarf durch neue Messwerte mit signifikantem Einfluss auch öfter. Die derzeit aktuelle Publikation wurde von Peter J. Mohr, Barry N. Taylor und David Newell herausgegeben.
Insgesamt wurden bis heute sechs Datensätze publiziert:
- CODATA 1973, E. Richard Cohen, Barry N. Taylor
- CODATA 1986 (Web Version 1.0 1994-10-06), E. Richard Cohen, Barry N. Taylor
- CODATA 1998 (Web Version 3.0 1999-07-23), Peter J. Mohr, Barry N. Taylor
- CODATA 2002 (Web Version 4.0 2003-12-09), Peter J. Mohr, Barry N. Taylor
- CODATA 2006 (Web Version 5.0 2007-03-07), Peter J. Mohr, Barry N. Taylor, David B. Newell
- CODATA 2010 (Web Version 6.0 2011-06-02)
Seit 1994 sind die CODATA-Empfehlungen im Internet verfügbar.
Details zu den CODATA-Werten sowie den zugrunde liegenden Messwerten und Berechnungsverfahren werden von den Autoren in der Regel anschließend im Journal Reviews of Modern Physics veröffentlicht. So wurden von Mohr und Taylor im Jahr 2000 die Details zu den CODATA 1998-Werten, 2005 die Details zu den Werten von CODATA 2002 und 2008 die von CODATA 2006 veröffentlicht.
Standardunsicherheiten von CODATA-Werten
CODATA-Werte werden mit einer Standardunsicherhei (en: standard uncertainty) angegeben. Das bedeutet, dass diese Art der Unsicherheit rechnerisch wie eine Standardabweichung behandelt werden kann. Die Unsicherheit u wird üblicherweise auf 2 signifikante Stellen gerundet angegeben.
u kann mit einem Erweiterungsfaktor (auch Abdeckungsfaktor genannt; en: coverage factor) k > 1 multipliziert werden, um den Vertrauensbereich zu erhöhen. Dieses Produkt wird dann als erweiterte Unsicherheit U bei einem bestimmten Erweiterungsfaktor bezeichnet:
- U = k · u
Allgemein werden erweiterte Unsicherheiten meist mit k = 2 angegeben; bei den CODATA-Werten ist in der Regel k = 1.
Die Unsicherheiten werden in einer statistischen Ausgleichsrechnung ermittelt, wobei man sich größtenteils an die Richtlinien des vom Joint Committee for Guides in Metrologyherausgegebenen Guide to the Expression of Uncertainty in Measurement (GUM) hält. Die CODATA verwendet für ihr Ausgleichsrechnungs-Verfahren den (englischen) Begriff least-squares adjustment (LSA).
In den CODATA-Tabellen ist die (absolute) Standardunsicherheit in kompakter Schreibweise gemäß den SI-Empfehlungen zur Darstellung von Größen in Klammern nach dem Zahlenwert angegeben. Beispielsweise ist die Angabe der Avogadro-Konstante nach CODATA 2010 in der Kurzform
gleichbedeutend zur langen Schreibweise der Form
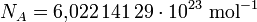 ;
;
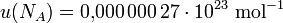
und sagt aus, dass die Standardunsicherheit 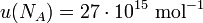 beträgt.
beträgt.
Daraus ergibt sich die relative Standardunsicherheit 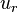 als Quotient von absoluter Standardunsicherheit und dem Betrag des Schätzwertes
der Größe. In oben genanntem Beispiel beträgt demnach
als Quotient von absoluter Standardunsicherheit und dem Betrag des Schätzwertes
der Größe. In oben genanntem Beispiel beträgt demnach
Die relativen Standardunsicherheiten des CODATA 2010-Datensatzes bewegen
sich in der Größenordnung von 10-12 (im besten Fall) bis
10-4 (im schlechtesten Fall). Die am besten schätzbare fundamentale
Konstante ist die Rydberg-Konstante
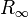 .
Diese nimmt daher in den CODATA-Ausgleichsrechnungen die zentrale Rolle ein,
sodass zunächst nur ihr Wert – unabhängig von den Unsicherheiten aller anderen
Konstanten – ermittelt wird. Weitere Schlüsselrollen in CODATA's least-squares
adjustment haben die Feinstrukturkonstante
α, das Plancksche Wirkungsquantum h und die universelle
Gaskonstante R, mit
.
Diese nimmt daher in den CODATA-Ausgleichsrechnungen die zentrale Rolle ein,
sodass zunächst nur ihr Wert – unabhängig von den Unsicherheiten aller anderen
Konstanten – ermittelt wird. Weitere Schlüsselrollen in CODATA's least-squares
adjustment haben die Feinstrukturkonstante
α, das Plancksche Wirkungsquantum h und die universelle
Gaskonstante R, mit
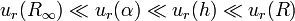 :
:
Die am schlechtesten schätzbare fundamentale Konstante ist die Newtonsche
Gravitationskonstante
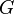 mit der hohen relativen Standardunsicherheit von
mit der hohen relativen Standardunsicherheit von 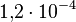 .
Diese wird daher gar nicht in CODATA's least-squares adjustment mit
einbezogen.
.
Diese wird daher gar nicht in CODATA's least-squares adjustment mit
einbezogen.
Abhängigkeiten zwischen Konstanten
Der Wert und die Standardunsicherheit vieler von der CODATA angegebener Größen ergibt sich durch mathematisch-statistische Umrechnung aus anderen von der CODATA angegebenen Größen. Sind alle Ausgangsgrößen voneinander unabhängig, so ergibt sich die Standardunsicherheit einer abgeleiteten Größe (Konstante) nach den Regeln des Gauß'schen Fehlerfortpflanzungsgesetzes. Bei einer Abhängigkeit (Korrelation) zwischen zwei (oder mehr) Konstanten muss das Fehlerfortpflanzungsgesetz um die Kovarianzen oder die Korrelationskoeffizienten r erweitert werden.
Allgemein kann die Korrelation zwischen zwei Größen bei einem Betrag ihres Korrelationskoeffizienten von | r | < 0,10 als fehlend und bei | r | > 0,90 als vollkommen betrachtet werden. Die meisten von der CODATA angegebenen Korrelationskoeffizienten zwischen zwei Konstanten fallen in eine dieser beiden Kategorien.
Auf der CODATA-Website ist zwar keine Liste von Korrelationskoeffizienten zu finden, doch ist es möglich, den Korrelationskoeffizienten (en: correlation coefficient) zwischen zwei beliebigen Konstanten gemäß der CODATA 2006-Anpassung online abzufragen.

Datum der letzten Änderung: Jena, den: 05.12. 2017