
Korrelationskoeffizient
Der Korrelationskoeffizient (auch: Korrelationswert) oder die
Produkt-Moment-Korrelation,
entwickelt von Auguste Bravais und Karl Pearson – daher auch
Bravais-Pearson-Korrelation oder Pearson-Korrelation genannt –,
ist ein dimensionsloses Maß
für den Grad des linearen Zusammenhangs zwischen zwei mindestens intervallskalierten
Merkmalen. Er
kann Werte zwischen
und
annehmen. Bei einem Wert von
(bzw.
)
besteht ein vollständig positiver (bzw. negativer) linearer Zusammenhang
zwischen den betrachteten Merkmalen. Wenn der Korrelationskoeffizient den Wert 0
aufweist, hängen die beiden Merkmale überhaupt nicht linear voneinander ab.
Allerdings können diese ungeachtet dessen in nichtlinearer Weise
voneinander abhängen. Damit ist der Korrelationskoeffizient kein geeignetes Maß
für die (reine) stochastische
Abhängigkeit von Merkmalen.
Je nachdem, ob der lineare Zusammenhang zwischen zeitgleichen Messwerten zweier verschiedener Merkmale oder derjenige zwischen zeitlich verschiedenen Messwerten eines einzigen Merkmals betrachtet wird, spricht man entweder von der Kreuzkorrelation oder von der Kreuzautokorrelation (siehe auch Zeitreihenanalyse).
Korrelationskoeffizienten wurden mehrfach – so schon von Ferdinand Tönnies – entwickelt, heute wird allgemein der von Karl Pearson verwendet.
Definitionen
Korrelationskoeffizient für Zufallsvariablen
Für zwei quadratisch integrierbare Zufallsvariablen
und
mit jeweils positiver Standardabweichung
bzw.
und Kovarianz
ist der Korrelationskoeffizient (Pearsonscher Maßkorrelationskoeffizient)
definiert durch:
Durch die Definitionen der stochastischen Varianz und Kovarianz lässt sich der Korrelationskoeffizient für Zufallsvariablen auch wie folgt darstellen
wobei
den Erwartungswert
darstellt. Weitere übliche Schreibweisen sind
und
.
Ferner heißen
unkorreliert, falls
gilt. Für positive
und
ist das genau dann der Fall, wenn
ist. Sind
unabhängig,
so sind sie auch unkorreliert, die Umkehrung gilt im Allgemeinen nicht.
Empirischer Korrelationskoeffizient
Für eine Messreihe von gepaarten Ausprägungen
wird der empirische Korrelationskoeffizient analog zum
Korrelationskoeffizienten für Zufallsvariablen berechnet, nur dass man nun die
empirische
Kovarianz und die empirischen
Varianzen der jeweiligen Zufallsvariablen verwendet:
Dabei sind
und
die empirischen Mittelwerte anhand der Messreihe.
Im Rahmen der induktiven
Statistik ist man an einer erwartungstreuen
Schätzung
der wahren, unbekannten Korrelation
in der Grundgesamtheit interessiert. Daher werden in die Formel der Korrelation
erwartungstreue
Schätzer der Varianzen und der Kovarianz eingesetzt. Dies führt zur
Formel:
Sind diese Messreihenwerte z-transformiert,
also ,
wobei
die erwartungstreue
Schätzung der Streuung bezeichnet, gilt auch:
Da man in der deskriptiven Statistik nur den Zusammenhang zwischen zwei Variablen als normierte mittlere gemeinsame Streuung in der Stichprobe beschreiben will, wird die Korrelation auch berechnet als
.
Da sich die Faktoren
bzw.
aus den Formeln herauskürzen, ergibt sich in beiden Fällen der gleiche Wert des
Koeffizienten.
Eine Vereinfachung der obigen Formel zur leichteren Berechnung einer Korrelation lautet wie folgt:
Beispiel
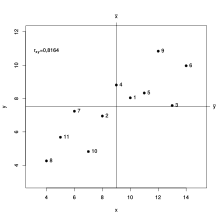
Für die elf Beobachtungspaare
sind die Werte in der unten stehenden Tabelle in der zweiten und dritten Spalte
gegeben. Die Mittelwerte ergeben sich zu
und
und damit können die vierte und fünfte Spalte der Tabelle berechnet werden. Die
sechste Spalte enthält das Produkt der vierten mit der fünften Spalte und damit
ergibt sich
.
Die beiden letzten Spalten enthalten jeweils die Quadrate der vierten und
fünften Spalte und es ergibt sich
und
.
Damit ergibt sich für die Korrelation .
| 1 | 10,00 | 8,04 | 1,00 | 0,54 | 0,54 | 1,00 | 0,29 |
| 2 | 8,00 | 6,95 | −1,00 | −0,55 | 0,55 | 1,00 | 0,30 |
| 3 | 13,00 | 7,58 | 4,00 | 0,08 | 0,32 | 16,00 | 0,01 |
| 4 | 9,00 | 8,81 | 0,00 | 1,31 | 0,00 | 0,00 | 1,71 |
| 5 | 11,00 | 8,33 | 2,00 | 0,83 | 1,66 | 4,00 | 0,69 |
| 6 | 14,00 | 9,96 | 5,00 | 2,46 | 12,30 | 25,00 | 6,05 |
| 7 | 6,00 | 7,24 | −3,00 | −0,26 | 0,78 | 9,00 | 0,07 |
| 8 | 4,00 | 4,26 | −5,00 | −3,24 | 16,20 | 25,00 | 10,50 |
| 9 | 12,00 | 10,84 | 3,00 | 3,34 | 10,02 | 9,00 | 11,15 |
| 10 | 7,00 | 4,82 | −2,00 | −2,68 | 5,36 | 4,00 | 7,19 |
| 11 | 5,00 | 5,68 | −4,00 | −1,82 | 7,28 | 16,00 | 3,32 |
| 99,00 | 82,51 | 55,01 | 110,00 | 41,27 | |||
| Alle Werte in der Tabelle sind auf zwei Stellen nach dem Komma gerundet! | |||||||
Eigenschaften
Mit der Definition des Korrelationskoeffizienten gilt unmittelbar
-
bzw.
.
.
Mit der Cauchy-Schwarzschen Ungleichung sieht man, dass
-
.
Durch Optimieren ergibt sich, dass
fast
sicher genau dann, wenn
.
Sind die Zufallsgrößen
und
stochastisch
voneinander unabhängig, dann gilt:
-
.
Der Umkehrschluss ist allerdings nicht zulässig, denn es können
Abhängigkeitsstrukturen vorliegen, die der Korrelationskoeffizient nicht
erfasst. Für die multivariate
Normalverteilung gilt jedoch: Die Zufallsvariablen
und
sind genau dann stochastisch unabhängig, wenn sie unkorreliert sind. Wichtig ist
hierbei die Voraussetzung, dass
und
gemeinsam
normalverteilt sind. Es reicht nicht aus, dass
und
jeweils normalverteilt sind.
Voraussetzungen für die Pearson-Korrelation
Der Korrelationskoeffizient nach Pearson erlaubt Aussagen über statistische Zusammenhänge unter folgenden Bedingungen:
Skalierung
Der Pearsonsche Korrelationskoeffizient liefert korrekte Ergebnisse bei intervallskalierten und bei dichotomen Daten. Für niedrigere Skalierungen existieren andere Korrelationskonzepte (z.B. Rangkorrelationskoeffizienten).
Normalverteilung
Für die Durchführung von standardisierten Signifikanztests über den Korrelationskoeffizienten in der Grundgesamtheit müssen beide Variablen annähernd normalverteilt sein. Bei zu starken Abweichungen von der Normalverteilung muss auf den Rangkorrelationskoeffizienten zurückgegriffen werden. (Alternativ kann man auch, falls die Verteilung bekannt ist, angepasste (nichtstandardisierte) Signifikanztests verwenden.)
Linearitätsbedingung
Zwischen den Variablen
und
wird ein linearer Zusammenhang vorausgesetzt. Diese Bedingung wird in der Praxis
häufig ignoriert; daraus erklären sich mitunter enttäuschend niedrige
Korrelationen, obwohl der Zusammenhang zwischen
und
bisweilen trotzdem hoch ist. Ein einfaches Beispiel für einen hohen
Zusammenhang trotz niedrigem Korrelationskoeffizienten ist die Fibonacci-Folge. Alle
Zahlen der Fibonacci-Folge sind durch ihre Position in der Reihe durch eine
mathematische Formel exakt determiniert (siehe die Formel von
Jacques-Philippe-Marie Binet in Fibonacci-Folge).
Der Zusammenhang zwischen der Positionsnummer einer Fibonacci-Zahl und der Größe
der Zahl ist vollkommen determiniert. Dennoch beträgt der
Korrelationskoeffizient zwischen den Ordnungsnummern der ersten 360
Fibonacci-Zahlen und den betreffenden Zahlen nur 0,20; das bedeutet, dass in
erster Näherung nicht viel mehr als 4 %
der Varianz durch den Korrelationskoeffizienten erklärt werden und 96 % der
Varianz „unerklärt“ bleiben. Der Grund ist die Vernachlässigung der
Linearitätsbedingung, denn die Fibonacci-Zahlen wachsen progressiv an: In
solchen Fällen ist der Korrelationskoeffizient nicht korrekt interpretierbar.
Eine mögliche Alternative, welche ohne die Voraussetzung der Linearität des
Zusammenhangs auskommt, ist die Transinformation.
Signifikanzbedingung
Ein Korrelationskoeffizient > 0 bei positiver Korrelation bzw. < 0 bei
negativer Korrelation zwischen
und
berechtigt nicht a priori zur Aussage, es bestehe ein statistischer
Zusammenhang zwischen
und
.
Eine solche Aussage ist nur gültig, wenn der ermittelte Korrelationskoeffizient
signifikant ist. Der Begriff „signifikant“ bedeutet hier „signifikant von
Null verschieden“. Je höher die Anzahl der Wertepaare
und das Signifikanzniveau sind, desto niedriger darf der Absolutbetrag
eines Korrelationskoeffizienten sein, um zur Aussage zu berechtigen, zwischen
und
gebe es einen linearen Zusammenhang. Ein t-Test
zeigt, ob die Abweichung des ermittelten Korrelationskoeffizienten von Null auch
signifikant ist.
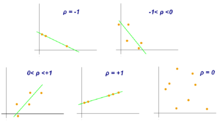
Bildliche Darstellung und Interpretation
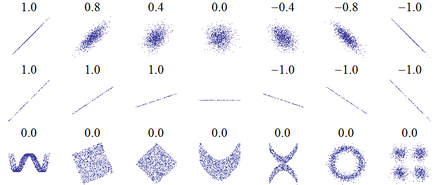
Sind zwei Merkmale vollständig miteinander korreliert (d.h. ),
so liegen alle Messwerte in einem 2-dimensionalen Koordinatensystem auf einer
Geraden. Bei einer perfekten positiven Korrelation (
)
steigt die Gerade. Wenn die Merkmale perfekt negativ miteinander korreliert sind
(
),
sinkt die Gerade. Besteht zwischen zwei Merkmalen eine sehr hohe Korrelation,
sagt man oft auch, sie erklären dasselbe.
Je näher der Betrag von
bei 0 liegt, desto kleiner der lineare Zusammenhang. Für
kann der statistische Zusammenhang zwischen den Messwerten nicht mehr durch eine
eindeutig steigende oder sinkende Gerade dargestellt werden. Dies ist z.B.
der Fall, wenn die Messwerte rotationssymmetrisch
um den Mittelpunkt verteilt sind. Dennoch kann dann ein nichtlinearer
statistischer Zusammenhang zwischen den Merkmalen gegeben sein. Umgekehrt gilt
jedoch: Wenn die Merkmale statistisch unabhängig sind, nimmt der
Korrelationskoeffizient stets den Wert 0 an.
Der Korrelationskoeffizient ist kein Indiz eines ursächlichen (d.h. kausalen) Zusammenhangs zwischen den beiden Merkmalen: Die Besiedlung durch Störche im Südburgenland korreliert zwar positiv mit der Geburtenzahl der dortigen Einwohner, doch das bedeutet noch keinen „kausalen Zusammenhang“, trotzdem ist ein „statistischer Zusammenhang“ gegeben. Dieser leitet sich aber aus einem anderen, weiteren Faktor ab, wie dies im Beispiel durch Industrialisierung oder der Wohlstandssteigerung begründet sein kann, die einerseits den Lebensraum der Störche einschränkten und andererseits zu einer Verringerung der Geburtenzahlen führten. Korrelationen dieser Art werden Scheinkorrelationen genannt.
Der Korrelationskoeffizient kann kein Indiz über die Richtung eines Zusammenhanges sein: Steigen die Niederschläge durch die höhere Verdunstung oder steigt die Verdunstung an, weil die Niederschläge mehr Wasser liefern? Oder bedingen sich beide gegenseitig, also möglicherweise in beiderlei Richtung?
Ob ein gemessener Korrelationskoeffizient als groß oder klein interpretiert wird, hängt stark von der Art der untersuchten Daten ab. Bei psychologischen Fragebogendaten werden z.B. Werte bis ca. 0,3 häufig als klein angesehen, ab ca. 0,5 als gut, während man ab ca. 0,7–0,8 von einer (sehr) hohen Korrelation spricht.
Das Quadrat des Korrelationskoeffizienten
nennt man Bestimmtheitsmaß.
Es gibt in erster Näherung an, wie viel Prozent der Varianz,
d.h. Streuung, der einen Variable durch die Streuung der anderen Variable
erklärt werden können. Beispiel: Bei r = 0,3 werden 9 % (= 0,3² = 0,09)
der gesamten auftretenden Varianz im Hinblick auf einen statistischen
Zusammenhang erklärt.
Fisher-Transformation
Empirische Korrelationskoeffizienten sind nicht normalverteilt. Vor der
Berechnung von Konfidenzintervallen
muss daher erst eine Korrektur der Verteilung mit Hilfe der
Fisher-Transformation vorgenommen werden. Wenn die Daten
und
aus einer zumindest annähernd bivariat
normalverteilten Grundgesamtheit stammen, dann ist der empirische
Korrelationskoeffizient
rechtssteil unimodal
verteilt.
Die Fisher-Transformation des Korrelationskoeffizienten
lautet dann:
ist annähernd normalverteilt mit der Standardabweichung
und Mittelwert
wobei
hier für den Korrelationskoeffizienten der Grundgesamtheit steht. Die auf Basis
dieser Normalverteilung errechnete Wahrscheinlichkeit, dass der Mittelwert von
den beiden Grenzen
und
umschlossen wird beträgt
,
und wird sodann retransformiert zu
Das -Konfidenzintervall
für die Korrelation lautet sodann
.
Konfidenzintervalle von Korrelationen liegen in aller Regel unsymmetrisch bezüglich ihres Mittelwerts.
Test des Korrelationskoeffizienten / Steigers Z-Test
Folgende Tests (Steigers Z-Test)
können durchgeführt werden, wenn die Variablen
und
annähernd bivariat normalverteilt sind:
| (zweiseitige Hypothese) | |
| (rechtsseitige Hypothese) | |
| (linksseitige Hypothese) |
Die Teststatistik ist
standardnormalverteilt
(
ist die Fisher-Transformation, siehe vorherigen Abschnitt).
Im Spezialfall der Hypothese
vs.
ergibt sich die Teststatistik als t-verteilt
mit
Freiheitsgeraden:
.
Partieller Korrelationskoeffizient
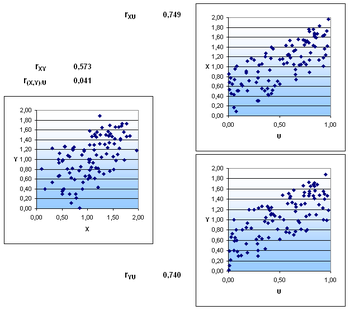
Eine Korrelation zwischen zwei Zufallsvariablen
und
kann unter Umständen auf einen gemeinsamen Einfluss einer dritten
Zufallsvariablen
zurückgeführt werden. Um solch einen Effekt zu messen, gibt es das Konzept der
partiellen Korrelation (auch Partialkorrelation genannt). Die „partielle
Korrelation von
und
unter
“
ist gegeben durch
Beispiel aus dem Alltag:
In einer Firma werden zufällig Mitarbeiter ausgewählt und die Körpergröße bestimmt. Zudem muss jeder Befragte sein Einkommen angeben. Das Ergebnis der Untersuchung ist, dass Körpergröße und Einkommen positiv korrelieren, also größere Personen auch mehr verdienen. Bei einer genaueren Untersuchung stellt sich jedoch heraus, dass der Zusammenhang auf die Drittvariable Geschlecht zurückgeführt werden kann. Frauen sind im Durchschnitt kleiner als Männer, verdienen aber auch oftmals weniger. Berechnet man nun die Partialkorrelation zwischen Einkommen und Körpergröße unter Kontrolle des Geschlechts, so verschwindet der Zusammenhang. Größere Männer verdienen demnach beispielsweise nicht mehr als kleinere Männer. Dieses Beispiel ist fiktiv und der Zusammenhang in der Realität komplizierter, es kann jedoch die Idee der Partialkorrelation veranschaulichen.
Robuste Korrelationskoeffizienten
Der Korrelationskoeffizient nach Pearson ist empfindlich gegenüber Ausreißern. Deswegen wurden verschiedene robuste Korrelationskoeffizienten entwickelt, z.B.
- der Spearmansche Rangkorrelationskoeffizient, da dieser Ränge statt der Beobachtungswerte nutzt oder
- die Quadrantenkorrelation.
Quadrantenkorrelation
Die Quadrantenkorrelation ergibt sich aus der Anzahl der Beobachtungen in den
vier vom Medianenpaar bestimmten Quadranten. Dazu zählt man, wie viele der
Beobachtungen in den Quadranten I und III liegen ()
bzw. wie viele sich in den Quadranten II und IV befinden (
).
Die Beobachtungen in den Quadranten I und III liefern jeweils einen Beitrag von
und die Beobachtungen in den Quadranten II und IV von
:
mit
der Signumfunktion,
der Zahl der Beobachtungen und
und
den Medianen
der Beobachtungen. Da jeder Wert von
entweder
,
oder
ist, spielt es keine Rolle wie weit eine Beobachtung von den Medianen entfernt
ist.
Über die Quadrantenkorrelation kann mit Hilfe des Median-Tests die Hypothesen
vs.
überprüft werden. Ist
die Zahl der Beobachtungen mit
,
die Zahl der Beobachtungen mit
und
,
dann ist folgende Teststatistik Chi-Quadrat-verteilt
mit einem Freiheitsgrad:
.
Schätzung der Korrelation zwischen nicht-metrischen Variablen
Die Schätzung der Korrelation mit dem Korrelationskoeffizienten nach Pearson setzt voraus, dass beide Variablen intervallskaliert und normalverteilt sind. Dagegen können die Rangkorrelationskoeffizienten immer dann zur Schätzung der Korrelation verwendet werden, wenn beide Variablen mindestens ordinalskaliert sind. Die Korrelation zwischen einer dichotomen und einer intervallskalierten und normalverteilten Variablen kann mit der punktbiserialen Korrelation geschätzt werden. Die Korrelation zwischen zwei dichotomen Variablen kann mit dem Vierfelderkorrelationskoeffizienten geschätzt werden. Hier kann man die Unterscheidung treffen, dass bei zwei natürlich dichotomen Variablen die Korrelation sowohl durch den Odds Ratio (OR) als auch durch den Phi-Koeffizient berechnet werden kann. Eine Korrelation aus zwei ordinal oder einer intervall und einer ordinal gemessenen Variablen ist mit Spearmans Rho oder Kendalls Tau berechenbar.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 09.09. 2025