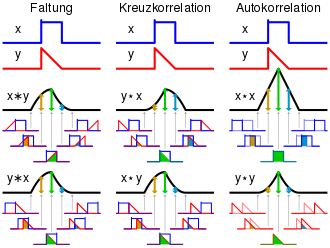
Kreuzkorrelation
In der Signalanalyse
wird die Kreuzkorrelationsfunktion
zur Beschreibung der Korrelation
zweier Signale
und
bei unterschiedlichen Zeitverschiebungen
zwischen den beiden Signalen eingesetzt. Kreuz steht hierbei für den Fall
der Funktion:
Handelt es sich um einen schwach stationären
Prozess, so ist die Korrelationsfunktion nicht mehr von der Wahl der
Zeitpunkte
und
,
sondern nur von deren Differenz
abhängig.
Definition
Es gilt für Energiesignale:
und für Leistungssignale:
mit
als der konjugiert
komplexen Funktion von
,
dem Operatorsymbol
als Kurzschreibweise der Kreuzkorrelation und
als dem der Faltungsoperation.
Analog wird die diskrete
Kreuzkorrelation, diese spielt im Bereich der diskreten Signalverarbeitung eine
wesentliche Rolle, mit der Folge
und einer Verschiebung
festgelegt als:
=
(Energiesignale)
=
(Leistungssignale)
In der digitalen Signalverarbeitung wiederum ist eine endliche Mittelung mit Argumenten beginnend bei Index 0 auf Grund der Architektur von Rechnerregistern erforderlich, wovon es eine vor- und eine unvorgespannte Version gibt:
(Vorspannversion)
(unvorgespannte Version)
Die Kreuzkorrelation ist mit der Kreuzkovarianz eng verwandt.
Eigenschaften
Für alle
gilt
sowie
und
mit den Autokorrelationsfunktionen
und
.
Sie zeigt z.B. Spitzen bei Zeitverschiebungen, die der Signallaufzeit
vom Messort des Signals
zum Messort des Signals
entsprechen. Auch Laufzeitunterschiede
von einer Signalquelle zu beiden Messorten können auf diese Weise festgestellt
werden. Die Kreuzkorrelationsfunktion eignet sich daher besonders zur Ermittlung
von Übertragungswegen und zur Ortung von Quellen.
Rechentechnisch wird die Kreuzkorrelationsfunktion in der Regel über die
inverse Fouriertransformation
des Kreuzleistungsspektrums
ermittelt:
Verbindung mit der Kreuzkovarianz
Ist eines der Signale
oder
nullsymmetrisch, d.h. ihr Mittelwert über das Signal ist Null
oder
,
ist die Kreuzkorrelation identisch mit der Kreuzkovarianz. Bekannte Vertreter
der nullsymmetrischen Funktionen sind zum Beispiel die Sinus- und
Kosinusfunktionen.
Literatur
- Bernd Girod, Rudolf Rabenstein, Alexander Stenger: Einführung in die Systemtheorie. 4. Auflage. Teubner, Wiesbaden 2007, ISBN 978-3-8351-0176-0.
- Rüdiger Hoffmann: Signalanalyse und -erkennung. Springer, ISBN 3-540-63443-6.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 27.05. 2021