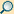Signalanalyse

Die Signalanalyse ermöglicht auf der Basis von Frequenzanalysen die Beschreibung der dynamischen Eigenschaften eines schwingenden Systems aus den Ein- und Ausgangssignalen dieses Systems. Sie ist neben statistischen Verfahren wie Mittelwertbildungen und der Berechnung von Standardabweichungen bei der Auswertung akustischer und schwingungstechnischer Signale von herausragender Bedeutung.

Häufig sind die zu analysierenden Systeme mechanische Strukturen. Dann könnten die Eingangsgröße eine anregende Kraft und die Ausgangsgrößen die resultierenden Oberflächenschnellen („Vibrationen“) an beliebigen Punkten auf der Struktur sein. Über die Signalanalyse lässt sich dann z.B. detailliert beschreiben, mit welchen Schwingschnellen die Struktur auf eine bestimmte Kraftanregung reagiert.

Ein weiteres breites Anwendungsgebiet der Signalanalyse besteht bei elektrischen Systemen, insbesondere bei Vierpolen. In diesem Fall kann die Eingangsgröße ein Strom oder eine Spannung sein. Die Ausgangsgröße ist in der Regel ebenfalls ein Strom oder eine Spannung. Bei großen elektrischen Systemen wie Maschinen oder Transformatoren lassen sich durch eine breitbandige Signalanalyse (siehe Übertragungsfunktion bzw. Frequenzgang) nicht nur elektrische, sondern auch mechanische Informationen (wie z.B. über Deformationen) ableiten.

Grundlagen

Darstellung eines dynamischen Systems mit Eingangs- und Ausgangsgröße

Die allgemeine Formulierung der Signalanalysetheorie geht von linearen Systemen aus. Durch spezielle Erweiterungen können jedoch auch nichtlineare Systeme behandelt werden.

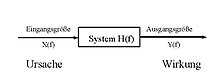
Basis der Signalanalyse ist die Fouriertransformation. Sie ermöglicht die Überführung von Zeitsignalen in den Frequenzbereich durch die Zerlegung der Zeitfunktionen in die Summe einer unendlichen Anzahl harmonischer Einzelfunktionen mit unendlich fein gestaffelten Frequenzen (Fourierintegral). Formulieren lässt sich dieser Zusammenhang für das Zeitsignal x(t) mit dem zugehörigen Fourierspektrum X(f) durch die Gleichung

$X(f)=\int _{-\infty }^{\infty }x(t)e^{-\mathrm {j} 2\pi ft}\,dt$

Die rechentechnische Darstellung dieser Transformation auf Digitalrechnern wird als Diskrete Fourier-Transformation (DFT) bezeichnet:

$X_{k}={\frac {1}{N}}\sum _{n=0}^{N-1}x_{n}e^{-j{\frac {2\pi nk}{N}}}$ (k=0, 1,…,N-1)

X_k wird als finites Fourierspektrum der diskretisierten Zeitfunktion x_n (N Abtastungen) bezeichnet. Der am häufigsten eingesetzte Algorithmus zu seiner Berechnung ist die Fast-Fourier-Transformation (FFT).

Illustration zur Diskreten Fourier-Transformation für ein Sinus-Signal mit der Frequenz 3,33 kHz (Analysefensterlänge: 0,3 ms, Abtastrate: 20 kHz)

Die numerische Berechnung bringt einige Besonderheiten mit sich, die bei der Signalanalyse beachtet werden müssen.

Durch die zeitdiskrete Abtastung (Diskretisierung) eines Messsignals ergeben sich bei gegenüber dem Frequenzgehalt des Signals zu kleinen Abtastfrequenzen Verzerrungen, die als Bandüberlappung oder Aliasing bezeichnet werden (Nyquist-Shannon-Abtasttheorem). Sie können durch analoge Tiefpassfilterung unterhalb der halben Abtastfrequenz („Anti-Aliasing-Filter“) vermieden werden.
Die Zeitbegrenzung der Abtastung („Zeit-“ oder „Analysefenster“) führt zum Auftreten von sog. Seitenbändern im Frequenzbereich. Entspricht die Beobachtungsdauer nicht der Periodendauer von im Signal enthaltenen Frequenzen oder deren ganzzahligen Vielfachen, so beeinflussen diese Seitenbänder das diskrete Spektrum z.B. durch das Auftreten zusätzlicher Frequenzkomponenten. Dieses Phänomen wird als Leck- oder Leakage-Effekt bezeichnet. Durch spezielle Bewertungsfunktionen im Zeitfenster (z.B. Hanning-Fenster) können seine Auswirkungen gemindert, jedoch nicht gänzlich vermieden werden.
Die Frequenzdiskretisierung bewirkt (nach Rücktransformation) eine Periodisierung des Zeitsignals, die jedoch meist ohne Bedeutung für die Analyse ist. Aus den unendlich fein gestaffelten Frequenzen des Fourierintegrals werden äquidistante ‚Frequenzlinien‘ mit Δf = 1/T.
Die Digitalisierung des Analogsignals führt zu einer Einschränkung des Dynamikbereiches, dem Quantisierungsrauschen, das sich als umso unbedeutender darstellt, je höher die Auflösung des A/D-Wandlers ist. Wegen der begrenzten Dynamik der analogen Messgeräte braucht dieser Effekt bei guter Aussteuerung während der Digitalisierung meist nicht beachtet zu werden.

Bei Beachtung dieser Besonderheiten stellt die DFT (FFT) ein leistungsfähiges Werkzeug zur Frequenzanalyse dar, das in den vergangenen Jahren analoge Techniken (Filterbänke) fast vollständig verdrängt hat. Auf ihr aufbauend lassen sich mit Hilfe der erweiterten Signalanalysetechniken besonders einfach die Beziehungen verschiedener Signale untereinander (typischerweise eines „Systemeingangs“ und mehrerer „Systemausgänge“) ermitteln. Voraussetzung hierfür ist i. Allg. die parallele Erfassung der Signale.

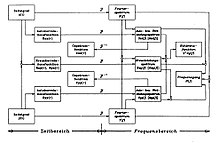
Im folgenden Bild sind die wichtigsten Signalanalysefunktionen in einem Blockdiagramm dargestellt. Anhand der Verbindungslinien kann prinzipiell der Berechnungsgang für die einzelnen Funktionen verfolgt werden. Im linken Bildteil sind die Zeitfunktionen, im rechten die Frequenzfunktionen angeordnet. Verknüpft sind die beiden Bereiche über die Fouriertransformation F bzw. die inverse Fouriertransformation F⁻¹, die sich für die Rückrechnung auf das Zeitsignal x(t) durch die Gleichung

$x(t)=\int _{-\infty }^{\infty }X(f)e^{\mathrm {j} 2\pi ft}\,df$

beschreiben lässt. Die inverse Fouriertransformation ermöglicht also die Bestimmung einer Zeitfunktion aus deren Fouriertransformierter. Die im Diagramm eingetragenen Vorwärts- und Rücktransformationen können demnach bei Bedarf auch jeweils in der anderen Richtung erfolgen. Weist ein Block mehrere Eingänge auf, so deutet dies auf mehrere Berechnungsmöglichkeiten hin.

Signalanalysefunktionen

Blockdiagramm mit den wichtigsten Signalanalysefunktionen

Die einzelnen Signalanalysefunktionen sind von unterschiedlicher Bedeutung. Herausragend sind das Autoleistungsspektrum, aus dem das RMS-Spektrum berechnet wird, der Frequenzgang, der das Systemverhalten beschreibt und z.B. zur Durchführung der Modalanalyse benötigt wird und die Kohärenz, mit der die Qualität der Analyseergebnisse beurteilt werden kann. Das Cepstrum dient zur Ermittlung von periodischen Anteilen und deren Ordnungen im Signal, ebenso in eingeschränkter Weise die Autokorrelationsfunktion. Mit der Kreuzkorrelationsfunktion lassen sich Laufzeiten zwischen Eingangs- und Ausgangssignal erkennen. Das Kreuzleistungsspektrum besitzt wenig eigene Aussagekraft. Es dient daher meist lediglich zur Bestimmung des Frequenzgangs und der Kreuzkorrelationsfunktion.

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de