
Zweitor
Ein Zweitor ist ein Modell für ein elektrisches Bauelement oder ein elektrisches Netzwerk mit vier Anschlüssen, bei dem je zwei Anschlüsse zu einem sogenannten Tor zusammengefasst werden.
Ein Tor liegt dann vor, wenn die elektrische Stromstärke durch beide Anschlüsse eines Tors gegengleich ist (Torbedingung). Ein Zweitor ist damit eine spezielle Form eines (allgemeinen) Vierpols.
Die Bezeichnung Vierpol stammt aus dem Jahr 1921 von Franz Breisig.
Die bei linearen Zweitoren übliche Matrizenschreibweise geht auf Felix Strecker und Richard Feldtkeller aus dem Jahr 1929 zurück.
Ein Zweitor ist andererseits ein Spezialfall eines n-Tores (welches auch als Mehrtor bezeichnet wird).
Allgemeines

Ein Zweitor ist eine spezielle Form eines Vierpols. Bei einem allgemeinen Vierpol muss die Torbedingung nicht gelten, womit die im nachfolgenden dargestellten Zweitorparameter und die mathematische Beschreibung mit Hilfe von Matrizen nur bei linearen Zweitoren und nicht bei allgemeinen Vierpolen anwendbar ist.
Vor allem in älterer Fachliteratur werden die Begriffe Zweitor und Vierpol synonym verwendet, wenngleich dabei unter dem Begriff Vierpol implizit Zweitore verstanden werden. Oft werden die Tore eines Zweitors auch als Eingang und als Ausgang bezeichnet.
Das Klemmenverhalten eines linearen Zweitors wird durch seine Übertragungsfunktion oder seinen Frequenzgang beschrieben. Hieraus lassen sich Zweitorgleichungen gewinnen, aus denen Zweitorparameter zur Modellbildung gewonnen werden können.
Eigenschaften
Zweitore lassen sich anhand der Eigenschaften ihres Klemmenverhaltens, d.h. als Blackbox ohne genaue Kenntnis ihrer inneren Struktur, wie folgt, klassifizieren:
Linearität
Die Übertragungsfaktoren von linearen Zweitoren sind unabhängig von Spannung und Strom. Deshalb gilt für die Torströme und -spannungen der Überlagerungssatz. Ein Zweitor, das nur aus den passiven linearen Bauelementen Widerstand, Spule, Kondensator und Übertrager besteht (ein sogenanntes RLCM-Zweitor), ist immer selbst linear.
Nichtlineare Zweitore sind Netzwerke mit mindestens einem nichtlinearen Bauelement und diese Bauelemente selbst, etwa Dioden oder Transistoren. Ihr Übertragungsverhalten hängt wesentlich von der Größe der Torströme und -spannungen ab. Eine annähernd lineare Beschreibung ist mittels der Kleinsignaltheorie bei stetigen Kennlinien und für kleine Amplituden möglich.
Nur lineare Zweitore sind Gegenstand der klassischen Vierpol- und der modernen Mehrtortheorie. Nur für sie gelten die linearen Zweitorgleichungen und damit die im Folgenden beschriebene Matrizendarstellung der Zweitorparameter.
Leistungsbilanz
Enthält ein Zweitor keine inneren ungesteuerten oder gesteuerten Energiequellen, so nennt man es passiv (z.B. Dämpfungsglied), anderenfalls aktiv. Daraus ergibt sich, dass die Ausgangswirkleistung P2 kleiner als die Eingangswirkleistung P1 sein muss. Aktive Vierpole, etwa Verstärker, entnehmen Energie aus Hilfsenergiequellen (Stromquelle).
Geht in einem (passiven) Zweitor keine Energie verloren, weil es nur Blindschaltelemente enthält, so nennt man es Reaktanzzweitor.
Umkehrbarkeit
Umkehrbare Zweitore (auch reziprok, kopplungssymmetrisch oder
übertragungssymmetrisch) haben in beide Richtungen dasselbe
Übertragungsverhalten, d.h. beispielsweise, dass sich das Verhältnis von
Ausgangsstrom und Eingangsspannung bei kurzgeschlossenem Ausgang beim
Vertauschen von Eingangs- und Ausgangsklemmenpaar nicht ändert. Diese
Eigenschaft wird auch als Reziprozitätstheorem oder als Kirchhoffscher
Umkehrungssatz bezeichnet. Somit erzeugt eine an Tor 1 angelegte Spannung
am kurzgeschlossenen Tor 2 einen Strom
.
Wird dieselbe Spannung an Tor 2 mit
angelegt, wird derselbe Strom
am kurzgeschlossenen Tor 1 erzeugt. Daraus ergibt sich
wenn
ist.
Reziproke Zweitore sind durch drei Zweitorparameter vollständig charakterisiert, denn für die Elemente der Zweitorgleichungen gelten dann folgende Einschränkungen:
Umkehrbarkeit ist nur für lineare Zweitore definiert. Ein Zweitor, das nur aus den passiven linearen Bauelementen Widerstand, Spule, Kondensator und Übertrager besteht (RLCM-Zweitor), ist immer umkehrbar.
Symmetrie
Bei symmetrischen Zweitoren (auch als widerstandssymmetrisch bezeichnet) sind Ein- und Ausgänge miteinander vertauschbar. Dies kann oft aus der Schaltung abgelesen werden. Wenn dies auf ein Zweitor nicht zutrifft, so wird dieses als unsymmetrisch bezeichnet.
Dabei gilt folgendes für die Elemente der Zweitorgleichungen:
Symmetrische Zweitore sind somit durch zwei Zweitorparameter vollständig charakterisiert. Symmetrische Zweitore sind immer reziprok, jedoch sind reziproke Zweitore nicht immer symmetrisch.
Erdungssymmetrie
Bei erdungssymmetrischen oder quersymmetrischen Zweitoren kann in Längsrichtung eine Symmetrielinie eingezeichnet werden. Das bedeutet, dass keine durchgehende Erdleitung vorhanden ist. Ein typisches Beispiel ist die sogenannte X-Schaltung eines Vierpols. Die in der Praxis als Zweitor verwendeten Dreipole haben dagegen eine durchgehende Erdleitung und sind deshalb erdungsunsymmetrisch. Die Eigenschaft der Erdungssymmetrie hat keinen Einfluss auf die Zweitorparameter. Theoretisch kann man mit Hilfe von idealen Übertragern erdungssymmetrische Zweitore in erdungsunsymmetrische und umgekehrt verwandeln.
Rückwirkungsfreiheit
Hat eine sich (durch Belastung) verändernde Ausgangsgröße keinen Einfluss auf eine Eingangsgröße, so nennt man das Zweitor rückwirkungsfrei. Rückwirkungsfreie Zweitore sind ein „Extremfall“ nichtumkehrbarer Zweitore.
Für die Parameter eines rückwirkungsfreien Zweitors gelten folgende Einschränkungen:
Damit sind die Eingangsgrößen ,
von den Ausgangsgrößen
,
unabhängig.
Zweitorgleichungen und Parameter
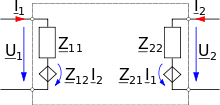
Bezeichnen U1 die Spannung und I1 den Strom am Eingangsklemmenpaar und U2 und I2 die entsprechenden Größen am Ausgangsklemmenpaar, dann können jeweils zwei gesuchte Größen aus den beiden anderen gegebenen Größen durch ein Paar von Zweitorgleichungen berechnet werden. Diese sind im Allgemeinen nichtlineare Differentialgleichungen.
Für lineare Zweitore gehen sie, eventuell unter Anwendung der symbolischen Methode der Wechselstromrechnung oder der Laplacetransformation, in ein Paar lineare Gleichungen mit vier das Zweitor beschreibenden Zweitorparametern über.
Unter der Voraussetzung der Existenz lassen sich diese Zweitorgleichungen in Form von Matrixgleichungen angeben. Eingeprägte Ströme und Spannungen werden je nach Bedarf zu diesen Gleichungen als Matrizen hinzu addiert. Die angegebenen Berechnungsvorschriften dienen zur Bestimmung der Matrizen für ein beliebiges, bekanntes Zweitor, wie zum Beispiel ein Feedback-Netzwerk einer Verstärkerschaltung.
| Z-Charakteristik | ||
| Y-Charakteristik | ||
| H-Charakteristik | ||
| P-Charakteristik | ||
| A-Charakteristik | ||
| B-Charakteristik |
Im Fall der Existenz der Matrizen gilt insbesondere:
Der Vorteil dieser Schreibweisen ist, dass die Parameter (Zxy, etc.) bekannte Bauteilwerte repräsentieren und daher als Zahlenwerte gegeben sind. Nun kann der Zusammenhang zwischen den Eingangs- und Ausgangsströmen, sowie den Eingangs- und Ausgangsspannungen leicht abgelesen werden.
Hinweis: Statt des Symbols
werden auch
oder
und statt des Symbols
wird auch
verwendet.
Umrechnung der Matrizen
Elementar-Zweitore
Elementar-Längszweitor
Das Elementar-Längszweitor enthält lediglich eine Impedanz in der oberen Längsachse zwischen den Ursprungspolen des Zweitors. Es gibt keine Verbindung zwischen den Polen in der Querachse.
Elementar-Querzweitor
Das Elementar-Querzweitor enthält lediglich eine Impedanz in der Querachse des Zweitors und enthält keine Bauelemente in der Längsachse.
Γ-Zweitor
Das Γ-Zweitor ist eine Synthese aus Elementar-Querzweitor und Elementar-Längszweitor. Es bildet sich aus den Kettenmatrizen der Elementar-Zweitore wie folgt:
Gespiegeltes Γ-Zweitor
Das gespiegelte Γ-Zweitor ist eine Synthese aus Elementar-Längszweitor und Elementar-Querzweitor. Es bildet sich aus den Kettenmatrizen der Elementar-Zweitore wie folgt:
Ersatzschaltungen
Zur Vereinfachung von Rechnungen können komplexe Zweitore mithilfe entsprechender Zweitorparameter zu vereinfachten Schaltungen zusammengefasst werden. Die Ersatzschaltungen stellen keine Anleitung zur physikalischen Realisierung dar.
T-Ersatzschaltung

Die T-Ersatzschaltung ermöglicht die Darstellung eines beliebigen Zweitors mithilfe der Ersatzimpedanzen. Bei umkehrbaren Zweitoren entfällt die gesteuerte Spannungsquelle. Es kann aus einem Elementar-Längszweitor und einem Γ-Zweitor oder entsprechend aus einem gespiegelten Γ-Zweitor und einem Elementar-Längszweitor synthetisiert werden. Nachfolgende Zusammensetzung beschreibt letzteres:
π-Ersatzschaltung

Die π-Ersatzschaltung ermöglicht die Darstellung eines beliebigen Zweitors mithilfe der Ersatzadmittanzen. Bei umkehrbaren Zweitoren entfällt die gesteuerte Stromquelle. Es kann aus einem Elementar-Querzweitor und einem gespiegelten Γ-Zweitor oder entsprechend aus einem Elementar-Querzweitor und einem Γ-Zweitor synthetisiert werden. Nachfolgende Zusammensetzung beschreibt letzteres:
Zusammenschalten
Zwei Zweitore können unter der Voraussetzung, dass die oben genannte Torbedingung an mindestens einem Tor erfüllt wird, zu einem neuen Zweitor zusammengeschaltet werden. Zur Überprüfung der Zulässigkeit der Zusammenschaltung dient der Brune-Test. Die Parameter des neu entstandenen Zweitors lassen sich aus den Parametern der beiden verschalteten Zweitore errechnen. Für jede Verschaltungsart gibt es eine Charakteristik, mit der sich die Verschaltung besonders gut berechnen lässt. Es gibt insgesamt fünf verschiedene Möglichkeiten Zweitore zusammenzuschalten:
| Beschreibungsart | Darstellung | Mathematische Beschreibung |
|---|---|---|
| Reihenschaltung | 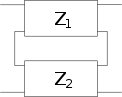 |
|
| Parallelschaltung | 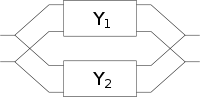 |
|
| Hybridschaltung oder Reihen-Parallelschaltung |
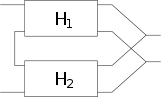 |
|
| inverse Hybridschaltung oder Parallel-Reihenschaltung |
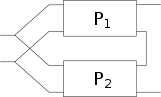 |
bzw. bzw. |
| Kettenschaltung | oder bzw. |
Vertauschen von Zweitoren
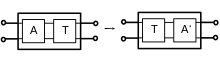
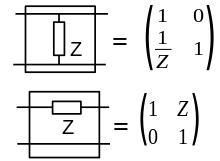
Oftmals ist es hilfreich ein Zweitor durch ein Anderes hindurch zu transformieren. Dafür seien die Zweitore A und T in Kettenparametern gegeben, T sei außerdem invertierbar und soll nicht verändert werden. Bei der Verschiebung durch T hindurch wird A nun zu A', sodass sich das Verhalten des Gesamtzweitors nicht ändert. Demzufolge muss gelten:
Eine besondere Rolle spielen hier die transformatorische Kopplung wo nur die Hauptdiagonale von T ist besetzt und die gyratorische Kopplung wo die Hauptdiagonale von T Null ist. Einfache Impedanzen können durch die nebenstehenden Matrizen in Kettenparametern ausgedrückt werden. Im Falle transformatorischer oder gyratorischer Kopplung sind dann A und A' von der Form her eine dieser beiden Matrizen, sprich eine einzelne Impedanz Z auf einer Seite von T kann durch eine einzelne Impedanz Z' auf der anderen Seite ausgedrückt werden. Bei der gyratorischen Kopplung werden dabei Parallel- zu Reihenschaltungen und umgekehrt. Auf diese Weise ist es möglich, ganze Netzwerke durch ein Zweitor hindurch zu projizieren.
Weitere Zweitorparameter
Neben der Charakterisierung eines Zweitors durch die oben beschriebenen Zweitorparameter gibt es für besondere Anwendungszwecke auch andere Darstellungsformen. So kann ein lineares Zweitor auch durch sogenannte Streuparameter beschrieben werden. Diese Darstellungsform ist vor allem im Bereich der Hochfrequenztechnik üblich, da dabei die Anschlüsse des Zweitors nicht kurzgeschlossen bzw. leerlaufen müssen, sondern im Regelfall durch ihre Wellenimpedanz abgeschlossen sind.
Zwischen den S-Parametern und den oben erwähnten Y-Parametern der Admittanzmatrix eines Zweitors besteht mit der Wellenimpedanz ZW folgender Zusammenhang:
mit der Abkürzung:
Symmetrische lineare Zweitore werden für ihre Anwendung in der Theorie der Siebschaltungen (Wellenparametertheorie) durch die sogenannten Wellenparameter beschrieben. Die zwei das Zweitor beschreibenden Parameter sind dabei die Wellenimpedanz und das Wellenübertragungsmaß.
Numerische CAD-Systeme in der Elektronik
Die praktische Auswertung und Verarbeitung obiger Matrizen aus komplexen Elementen erfordert den Einsatz von Rechnern. Seit den 1970er-Jahren wird von der rechnergestützten numerischen Auswertung und Weiterverarbeitung obiger Gleichungen berichtet, und ab den 1980er-Jahren setzten sich dann aufwendige numerische CAD-Systeme (z.B. Super-Compact) schrittweise in der Industrie durch. Dabei besteht kein grundsätzlicher Unterschied zwischen der Hochfrequenz- und Mikrowellenelektronik und der Elektronik bei tieferen Frequenzen. Die linearen Abhängigkeiten zwischen Strom und Spannung wird bei allen Frequenzen durch die obigen sechs Vierpolformen und völlig gleichwertig durch s- und t-Parameter (eine s-Parameter-Kettenform) beschrieben, solange überhaupt die Begriffe von Strom und Spannung als „Ersatzgrößen“ anstelle der elektromagnetischen Felder und anderer physikalischer Begriffe genommen werden können. In vielen Fällen ist dies bis in den Mikrowellenbereich möglich, ohne dass mit erheblich mehr Rechenaufwand vollnumerisch die Feldgleichungen für die elektromagnetischen Felder zu lösen wären. Der Übergang ist dabei aber stets fließend.
Symbolische CAD-Systeme für rechnergestützte Formelherleitungen
Von Interesse ist weiterhin auch die symbolische Verarbeitung obiger Matrizengleichungen und darauf aufbauend die rechnergestützte Formelherleitung für die Signalanalyse in der linearen Elektronik und Hochfrequenzelektronik. Ein spezieller Zusatz für ein Mathematikprogramm wandelt dabei die obigen acht Vierpolparameterdarstellungen zuzüglich der Wellenparameterform und ergänzt durch zahlreiche weitere Modelle (aktive Elemente wie Einzeltransistoren und Standardschaltungen sowie passive Elemente wie Leitung, Transformator, Koppler, Richtungsleitung: alle mit ihren jeweiligen Modellparametern) symbolisch und – so weit dies logisch möglich ist – von jeder Art in jede andere Art um. Die obige Vernetzung von Vierpolen wird dabei weitgehend automatisiert und durch weitere Befehle ergänzt wie z.B. das Deembedden eines eingebetteten Vierpols, das obige Durchschieben eines Vierpols durch einen anderen Vierpol hindurch, verschiedene Anschlußklemmenvertauschungen et cetera. Als Ergebnis erhält man dann von den Modellparametern und/oder den Vierpolparametern abhängige Formeln für die üblichen Reportgrößen, die bei den numerischen CAD-Systemen nur als Zahlen erscheinen: Formelsätze für Spannungs- und Stromverstärkung, Eingangs- und Ausgangsimpedanzen, Reflexionsfaktoren, Gewinngrößen oder Stabilitätsfaktor bis hin zu den verallgemeinerten Streuparametern nach Kurokawa, also für Größen, die in den numerischen Systemen Standard sind. Ein solches System ist faszinierend und eignet sich auch sehr, um neue Zusammenhänge zu erarbeiten, Ideen zu entwickeln oder Vermutungen zu beweisen bzw. zu widerlegen.
Möglichkeiten und Grenzen der CAD-Systeme
Trotz der enormen Möglichkeiten bleiben diese symbolischen ebenso wie die numerischen CAD-Systeme immer nur Rechenassistenten, die stets mit viel Sachverstand geführt werden müssen, denn sie bestehen aus mathematischen Theorien, Modellen und vielen Programmzeilen. Die Qualität aller Rechenergebnisse steht und fällt dabei immer mit der Messung.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 17.09. 2023