Autokorrelation
Die Autokorrelation (auch Kreuzautokorrelation)
ist ein Begriff aus der Statistik
und der Signalverarbeitung
und beschreibt die Korrelation
einer Funktion oder eines Signals mit sich selbst zu einem früheren Zeitpunkt.
Korrelationsfunktionen werden für Folgen von Zufallsvariablen
berechnet, die von der Zeit
abhängen. Diese Funktionen geben an, wie viel Ähnlichkeit die um die Zeit
verschobene Folge
mit der ursprünglichen Folge
hat. Da die unverschobene Folge mit sich selbst am ähnlichsten ist, hat die
Autokorrelation für die unverschobene Folge
den höchsten Wert. Wenn zwischen den Gliedern der Folge eine Beziehung besteht,
die mehr als zufällig ist, hat auch die Korrelation der ursprünglichen Folge mit
der verschobenen Folge in der Regel einen Wert, der signifikant von Null
abweicht. Man sagt dann, die Glieder der Folge sind autokorreliert.
Allgemeines
Da die Folge
mit einer verschobenen Version ihrer selbst verglichen wird, spricht man von
einer Autokorrelation. Werden hingegen zwei verschiedene Folgen
und
verglichen, spricht man von einer Kreuzkorrelation.
Mit der Autokorrelation ist es möglich, Zusammenhänge zwischen den beobachteten
Ergebnissen zu verschiedenen Beobachtungszeitpunkten einer Messreihe
festzustellen. Die Kreuzkorrelation gibt dagegen die Korrelation zwischen
verschiedenen Merkmalen in Abhängigkeit von der Zeit an.
In der Signalverarbeitung geht man häufig auch von kontinuierlichen Messdaten
aus. Man spricht von Autokorrelation, wenn die kontinuierliche oder zeitdiskrete
Funktion (z.B. ein- oder mehrdimensionale Funktion über die Zeit oder den
Ort) mit sich selbst korreliert wird, beispielsweise
mit
.
Mit dem Durbin-Watson-Test
kann anhand einer Stichprobe überprüft werden, ob eine Zeitreihe oder räumliche
Daten eine Autokorrelation aufweisen.
Die Autokorrelation wird in den verschiedenen Disziplinen unterschiedlich
definiert. In der Statistik wird sie für stochastische
Prozesse
als normierte Form der Autokovarianz berechnet, in der Signalverarbeitung als Faltung
des zeitabhängigen Signals
mit sich selbst. In manchen Gebieten werden die Begriffe Autokorrelation und
Autokovarianz auch synonym verwendet.
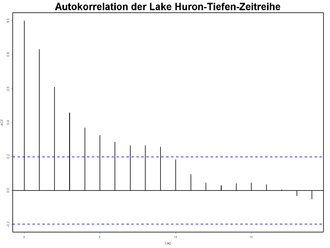
In einem Korrelogramm kann die Autokorrelation grafisch dargestellt werden.
Autokovarianz und Autokorrelation in der Statistik
Die Autokovarianzfunktion beschreibt die Kovarianz
zwischen den Werten eines stochastischen
Prozesses zu verschiedenen Zeiten. Für einen reellwertigen
stochastischen Prozess
ist sie definiert als:
Hierbei bezeichnet
den Erwartungswert
und
Erwartungswert von
.
Die Existenz dieser Erwartungswerte wird vorausgesetzt. Für eine Zeitdifferenz
ist die Autokovarianz identisch mit der Varianz.
Für einen stationären
Prozess
sind die statistischen Größen Erwartungswert, Standardabweichung und Varianz der
Zufallsvariable
nicht mehr zeitabhängig. Die Autokovarianz ist dann nicht von der Lage der
Zeitpunkte, sondern nur von der Zeitdifferenz
zwischen
und
abhängig:
Die Autokorrelationsfunktion des stochastischen Prozesses wird definiert als normierte Autokovarianzfunktion:
-
- Hierbei bedeuten:
-
-
Standardabweichung von Standardabweichung von Autokorrelation bezogen auf die Zeitpunkte und
-
In dieser Form ist die Autokorrelationsfunktion einheitenlos und auf den Bereich zwischen −1 und 1 normiert.
Für einen stationären Prozess ist die Autokovarianz nur vom Zeitunterschied
zwischen
und
abhängig. Die Standardabweichung ist dann unabhängig vom Zeitpunkt, das Produkt
der Standardabweichungen im Nenner entspricht dann der von
unabhängigen Varianz
.
Somit vereinfacht sich die Autokorrelationsfunktion für einen stationären
Prozess zu:
,
da
gilt.
Autokorrelation in der Signalverarbeitung
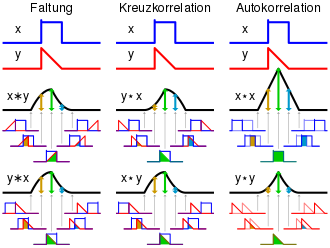
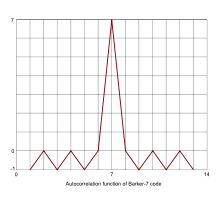
Hier wird die Autokorrelationsfunktion (AKF) zur Beschreibung der Korrelation eines Signales
mit sich selbst bei unterschiedlichen Zeitverschiebungen
zwischen den betrachteten Funktionswerten eingesetzt. Die AKF des Signals lässt
sich sowohl symmetrisch um den Nullpunkt herum definieren:
,
als auch asymmetrisch:
,
Das Ergebnis ist jedoch in beiden Fällen gleich.
In Kurzschreibweise wird für die Autokorrelation das Operatorsymbol
verwendet:
mit
als die konjugiert
komplexe Funktion von
und dem Faltungsoperator
.
Die AKF entspricht der Autokovarianzfunktion für mittelwertfreie, stationäre Signale. In der Praxis wird die Autokorrelationsfunktion solcher Signale in der Regel über die Autokovarianzfunktion berechnet.
Für zeitdiskrete Signale wird statt des Integrals die Summe verwendet. Mit
einer diskreten Verschiebung
ergibt sich:
In der digitalen Signalanalyse wird die Autokorrelationsfunktion in der Regel
über die inverse
Fouriertransformation des Autoleistungsspektrums
(z.B. )
berechnet:
Die theoretische Grundlage dieser Berechnung ist das Wiener-Chintschin-Theorem.
Impuls-AKF
Für Signale mit endlichem Energieinhalt – sogenannte Energiesignale – erweist es sich als sinnvoll, folgende Definition zu verwenden:
.
Eigenschaften
Geradheit
Die AKF ist eine gerade Funktion:
.
AKF und Periodizitäten
Die einer periodischen AKF ()
zugrundeliegende Funktion
ist selbst periodisch, wie folgender Beweis zeigt:
-
.
Umgekehrt gilt auch für periodische Funktionen ,
dass ihre AKF
periodisch ist:
-
.
Somit lässt sich schließen, dass eine Funktion und ihre AKF stets dieselbe Periodizität aufweisen:
.
Gibt es Wiederholungen im Signal, so ergeben sich Maxima der Autokorrelationsfunktion bei den Zeitverschiebungen, die der Wiederholungsdauer von Erscheinungen im Signal entsprechen. So können z.B. versteckte periodische Anteile und Echoerscheinungen in Signalen detektiert werden.
Maximum
Die AKF hat unabhängig ihrer Definition bei
ihr Maximum:
Für die AKF wird dieser Wert als Effektivwertquadrat, für die Impuls-AKF als Signalenergie bezeichnet.
Häufig wird die Autokorrelationsfunktion auch auf den Maximalwert bei
normiert angegeben:
Der Betrag
dieser normierten Autokorrelationsfunktion kann Werte zwischen 0 und 1 annehmen.
Man spricht dabei auch vom zeitlichen Autokorrelationskoeffizienten
einer Zufallsvariablen
mit der zeitlich verschobenen Zufallsvariablen
.
Abfallverhalten
Für große Zeiten
und nicht selbst periodische Funktionen x gilt:
.
Beispiele

Beispiel 1
Die Funktionen im nebenstehenden Bild sind aus sinusförmigen Abschnitten einheitlicher Frequenz zusammengesetzt. An den Stoßstellen treten Phasensprünge auf. Zur Berechnung der Korrelation multipliziert man punktweise beide Signalwerte und addiert die Produkte über einen längeren Zeitraum. Bei der gezeichneten Verzögerung Δs sind in den rot markierten Bereichen alle Einzelprodukte positiv oder null, in den dazwischen liegenden Bereichen meist negativ. Nur für Δs = 0 sind alle Einzelprodukte positiv, die Korrelationsfunktion erreicht ihren maximalen Wert.
Nebenbemerkung: Addiert man beide Signale, können stückweise konstruktive bzw. destruktive Interferenz auftreten.
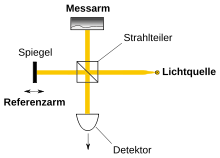
Beispiel 2
Bei der Optischen Kohärenztomografie wird Licht besonders geringer Kohärenzlänge verwendet, weil die Autokorrelation nur dann ein merklich von Null abweichendes Ergebnis liefert, wenn die Länge von Messarm und Referenzarm gut übereinstimmen. Bei größerer Abweichung variieren die Ergebnisse der Autokorrelation um Null (Weißlichtinterferometrie).
Schätzung
Analog zur Stichprobenkovarianz
und Stichprobenkorrelation
können auch die Stichprobenautokovarianz bzw. die Stichprobenautokorrelation
bestimmt werden. Liegen die Daten
einer stationären Zeitreihe vor, wird die unkorrigierte azyklische
Stichprobenautokovarianz üblicherweise durch
geschätzt, wobei .
Zu beachten ist hier die Konvention, die Summe durch
statt durch
zu teilen, um zu garantieren, dass die Folge der Stichprobenautokovarianzen positiv
semidefinit ist.
Für
erhält man die unkorrigierte Stichprobenvarianz
der Daten.
Die Stichprobenautokorrelation ergibt sich dann durch
mit .
Die Berechnung der Standardfehler
von Stichprobenautokorrelationen erfolgt meist anhand der Bartlett-Formel.
Um die unverzerrte
azyklische Stichprobenautokorrelation zu berechnen, teilt man stattdessen durch
:
Die unverzerrte azyklische Stichprobenkorrelation kann auf modernen Computern schneller im Fourierraum ausgerechnet werden, indem das Signal mit Nullen verlängert ("Zero Padding"). Die angehängten Nullen bewirken, dass nicht die zyklische Stichprobenkorrelation berechnet wird (welche ein periodisches Signal annimmt), sondern die azyklische Stichprobenkorrelation:
Anwendungen
Genutzt wird die Autokorrelation u.a. in der Regressionsanalyse, der Zeitreihenanalyse und in der Bildverarbeitung. Beispielsweise werden in der Regressionsanalyse die Störgrößen, also die Abweichungen der Beobachtungswerte von der wahren Regressionsgeraden, als Folge von identisch verteilten Zufallsvariablen interpretiert. Damit die Regressionsanalyse sinnvolle Ergebnisse liefert, müssen die Störgrößen unkorreliert sein. In der Zeitreihenanalyse wird die Autokorrelationsfunktion zusammen mit der partielle Autokorrelationsfunktion häufig zur Identifikation von ARMA-Modellen verwendet.
Finden von Signalperioden
Eine häufige Anwendung der Autokorrelationsfunktion besteht darin, in stark verrauschten Signalen Periodizitäten zu finden, die nicht ohne weiteres ersichtlich sind:
- Die Autokorrelationsfunktion eines periodischen Signals ist wieder ein periodisches Signal mit derselben Periode So ist zum Beispiel die Autokorrelationsfunktion eines Kosinussignals
-
- wiederum eine Kosinusfunktion mit derselben Kreisfrequenz
(Erhaltung der Signalperiode).
,
- Allerdings ist hierbei die Phaseninformation verloren gegangen.
- Eine gleichwertige Möglichkeit des Findens der Signalperiode ist die Möglichkeit, das Fourier-Spektrum des Signals nach einer dominanten Frequenz zu untersuchen. Da die Autokorrelation die normierte Fourier-Transformierte des Leistungsdichtespektrum ist (gemäß dem Wiener-Khinchine-Theorem), sind beide Ansätze gleichwertig.
- Da weißes
Rauschen zu einem Zeitpunkt völlig unabhängig von weißem Rauschen zu einem
anderen Zeitpunkt ist, ergibt die Autokorrelationsfunktion von weißem Rauschen
einen Dirac-Impuls
an der Stelle
. Liegt weißes Rauschen der Leistungsdichte
für die Frequenzen
vor, so gilt:
Bei gefärbtem Rauschen, das in technischen Systemen meistens an Stelle von weißem Rauschen vorkommt, ergibt sich ebenso ein absolutes Maximum der Autokorrelationsfunktion beiund ein Abfall der Autokorrelationsfunktion für Verschiebungen
. Die Breite dieses Maximums wird von der "Farbe" des Rauschens bestimmt.
Bei der Analyse von Periodizitäten wird nur die Autokorrelationsfunktion für
große Werte von
betrachtet und der Bereich um
ignoriert, da er vor allem Information über die Stärke des Rauschsignals
enthält.
Signal-Rausch-Verhältnis
Da der Wert der Autokorrelationsfunktion bei
dem quadratischen Mittelwert (bei Leistungssignalen) bzw. der Signalenergie (bei
Energiesignalen) entspricht, kann man durch Bilden der Autokorrelationsfunktion
relativ einfach das Signal-Rausch-Verhältnis
abschätzen.
Dazu teilt man die Höhe des Wertes ,
d.h. den Wert, den die Autokorrelationsfunktion ohne Rauschen an der
Stelle 0 hätte, durch die Höhe der „Rauschspitze“. Beim Umrechnen des
Signal-Rausch-Verhältnisses Sx / Nx in Dezibel
muss man darauf achten, dass man
und nicht
verwendet. Das liegt daran, dass die Autokorrelationsfunktion an der Stelle 0
eine Leistungs- bzw. Energiegröße (quadratische Größe) und keine Feldgröße
darstellt.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 15.04. 2022