Zeitdiskretes Signal
Ein zeitdiskretes Signal, manchmal auch nur als diskretes Signal bezeichnet, ist eine spezielle Form eines Signals, das nur zu bestimmten, üblicherweise äquidistanten Zeitpunkten definiert ist. Es wird aus einem zeitkontinuierlichen Signal dadurch gewonnen, dass dem zeitkontinuierlichen Signalverlauf zu bestimmten Zeitpunkten ein Signalwert entnommen wird. Jeder Signalwert ist wertkontinuierlich und kann in seiner Auflösung beliebig genau sein. Ein zeitdiskretes Signal kann dann durch eine zusätzliche Quantisierung der einzelnen Signalwerte, das bedeutet eine Reduzierung des Wertevorrates auf eine bestimmte, endliche Anzahl von Niveaus, in ein Digitalsignal umgewandelt werden.
Zeitdiskrete Signale spielen in der Signaltheorie und der Informationstheorie zur Systembeschreibung und als Vorstufe zur digitalen Signalverarbeitung eine bedeutende Rolle.
Allgemeines
Ein zeitdiskretes Signal kann mathematisch als eine Folge
x[n] von reellen
Zahlen mit
beschrieben werden. Der Index n stellt die auf die Abtastrate normierte
Zeitvariable dar – üblicherweise erfolgt die Abtastung zu konstanten zeitlichen
Abständen Ts. Der Kehrwert
wird als Abtastrate oder als
Abtastfrequenz fs bezeichnet. Die Werte des zeitdiskreten
Signal zwischen zwei Abtastzeitpunkten
und
sind nicht Null, sondern sind nicht definiert.
Das Nyquist-Shannon-Abtasttheorem beschreibt in diesem Fall den Effekt, dass in der Folge x[n] dann die vollständige Information des kontinuierlichen Signalverlaufs enthalten ist, wenn dessen höchsten Frequenzanteile fa kleiner als die halbe Abtastfrequenz fs sind:
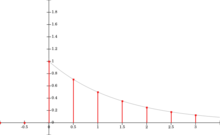
Ein kontinuierliches Signal kann, als Beispiel und in der rechten Abbildung dargestellt, durch die Funktion
beschrieben werden. Das daraus abgeleitete zeitdiskrete Signal ist mit roten vertikalen Linien kennzeichnet und lässt sich ausdrücken als:


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 31.07. 2022