
Chi-Quadrat-Verteilung
Die Chi-Quadrat-Verteilung (-Verteilung)
ist eine stetige
Wahrscheinlichkeitsverteilung
über der Menge der nicht-negativen reellen Zahlen. Üblicherweise ist mit
„Chi-Quadrat-Verteilung“ die zentrale Chi-Quadrat-Verteilung gemeint. Ihr
einziger Parameter
muss eine natürliche
Zahl sein und wird Freiheitsgrad
genannt.
Sie ist eine der Verteilungen, die aus der Normalverteilung
abgeleitet werden können: Hat man
Zufallsvariablen
,
die unabhängig und standardnormalverteilt
sind, so ist die Chi-Quadrat-Verteilung mit
Freiheitsgraden definiert als die Verteilung der Summe der quadrierten
Zufallsvariablen
.
Solche Summen quadrierter Zufallsvariablen treten bei Schätzfunktionen wie der
Stichprobenvarianz
zur Schätzung der Varianz
einer Stichprobe auf. Die
Chi-Quadrat-Verteilung ermöglicht damit unter anderem ein Urteil über die
Kompatibilität eines vermuteten funktionalen Zusammenhangs (Abhängigkeit von der
Zeit, Temperatur, Druck etc.) mit empirisch ermittelten Messpunkten. Kann
z.B. eine Gerade die Daten erklären, oder braucht man doch eine Parabel
oder vielleicht einen Logarithmus? Man wählt verschiedene Modelle aus, und
dasjenige mit der besten Anpassungsgüte,
dem kleinsten
,
bietet die beste Erklärung der Daten.
So stellt die
-Verteilung
durch die Quantifizierung der zufälligen Schwankungen die Auswahl verschiedener
Erklärungsmodelle auf eine numerische Basis. Außerdem erlaubt sie, wenn man die
empirische
Varianz bestimmt hat, die Schätzung des Vertrauensintervalls,
das den (unbekannten) Wert der Varianz der Grundgesamtheit mit einer gewissen
Wahrscheinlichkeit einschließt. Diese und weitere Anwendungen sind weiter
unten und im Artikel Chi-Quadrat-Tests
beschrieben.
Die Chi-Quadrat-Verteilung wurde 1876 eingeführt von Friedrich Robert Helmert, die Bezeichnung stammt von Karl Pearson (1900).
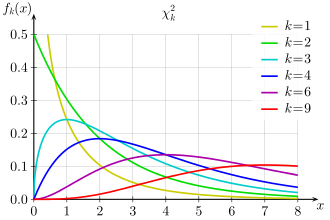
Definition
Die Chi-Quadrat-Verteilung mit
Freiheitsgraden beschreibt die Verteilung
der Summe
stochastisch
unabhängiger quadrierter standardnormalverteilter
Zufallsvariablen
, mit
für
.
Das Zeichen
ist eine Kurzschreibweise für „ist verteilt wie“. Die Summe quadrierter
Größen kann keine negativen Werte annehmen.
Im Unterschied dazu gilt für die einfache Summe
mit um den Nullpunkt symmetrischer Verteilung.
Dichte
Die Dichte
der
-Verteilung
mit
Freiheitsgraden hat die Form:
Dabei steht
für die Gammafunktion.
Die Werte von
kann man mit
.
berechnen.
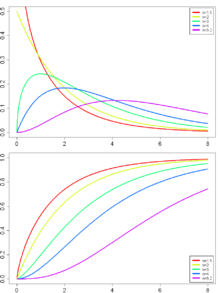
Verteilungsfunktion
Die Verteilungsfunktion kann man mit Hilfe der regularisierten unvollständigen Gammafunktion schreiben:
Wenn
eine natürliche Zahl ist, dann kann die Verteilungsfunktion (mehr oder weniger)
elementar dargestellt werden:
wobei
die Fehlerfunktion
bezeichnet. Die Verteilungsfunktion beschreibt die Wahrscheinlichkeit, dass
im Intervall
liegt.
Eigenschaften
Erwartungswert
Der Erwartungswert
der Chi-Quadrat-Verteilung mit
Freiheitsgraden ist
.
Unter der Voraussetzung einer standardnormalverteilten Grundgesamtheit sollte
also bei richtiger Abschätzung der Varianz der Grundgesamtheit der Wert
in der Nähe von 1 liegen.
Varianz
Die Varianz
der Chi-Quadrat-Verteilung mit
Freiheitsgraden ist
.
Modus
Der Modus
der Chi-Quadrat-Verteilung mit
Freiheitsgraden ist
für
.
Schiefe
Die Schiefe
der Chi-Quadrat-Verteilung mit
Freiheitsgraden ist
.
Die Chi-Quadrat-Verteilung besitzt eine positive Schiefe, d.h., sie ist
linkssteil- bzw. rechtsschief. Je höher die Anzahl der Freiheitsgrade ,
desto weniger schief ist die Verteilung.
Kurtosis
Die Kurtosis
(Wölbung)
der Chi-Quadrat-Verteilung mit
Freiheitsgraden ist gegeben durch
.
Der Exzess
gegenüber der Normalverteilung ergibt sich damit zu
.
Daher gilt: Je höher die Anzahl der Freiheitsgrade
,
desto geringer der Exzess.
Momenterzeugende Funktion
Die momenterzeugende
Funktion für
hat die Form
.
Charakteristische Funktion
Die charakteristische
Funktion für
ergibt sich aus der momenterzeugenden Funktion als:
.
Entropie
Die Entropie der Chi-Quadrat-Verteilung (ausgedrückt in nats) beträgt
wobei ψ(p) die Digamma-Funktion bezeichnet.
Summe
 -verteilter
Zufallsvariablen
-verteilter
Zufallsvariablen
Sind
unabhängige,
-verteilte
Zufallsvariablen, mit
,
so gilt:
.
Darin sind die
standardnormalverteilten Zufallsvariablen
unabhängig, und deshalb ist die Summe wieder
-verteilt.
Die Chi-Quadrat-Verteilung ist also reproduktiv.
Nichtzentrale Chi-Quadrat-Verteilung
Wenn die normalverteilten Zufallsvariablen nicht bezüglich ihres Erwartungswertes
zentriert sind (d.h., wenn nicht alle
sind), erhält man die nichtzentrale Chi-Quadrat-Verteilung. Sie hat als zweiten
Parameter neben
den Nichtzentralitätsparameter
.
Seien ,
so ist
mit
.
Insbesondere folgt aus
und
,
dass
ist.
Eine zweite Möglichkeit, eine nichtzentrale Chi-Quadrat-Verteilung zu erzeugen, ist als Mischverteilung der zentralen Chi-Quadrat-Verteilung. Dabei ist
,
wenn
aus einer Poisson-Verteilung
gezogen wird.
Dichtefunktion
Die Dichtefunktion der nichtzentralen Chi-Quadrat-Verteilung ist
für
,
für
.
Die Summe über j führt auf eine modifizierte Bessel-Funktion
erster Gattung
. Damit erhält die Dichtefunktion folgende Form:
für
.
Erwartungswert und Varianz der nichtzentralen Chi-Quadrat-Verteilung
und
gehen ebenso wie die Dichte selbst bei
in die entsprechenden Ausdrücke der zentralen Chi-Quadrat-Verteilung über.
Verteilungsfunktion
Die Verteilungsfunktion der nichtzentralen Chi-Quadrat-Verteilung kann mit
Hilfe der Marcum-Q-Funktion
ausgedrückt werden.
Beispiel
Man macht
Messungen einer Größe
,
die aus einer normalverteilten Grundgesamtheit stammen. Sei
der Mittelwert der
gemessenen Werte und
die korrigierte
Stichprobenvarianz. Dann lässt sich z.B. das 95 %-Konfidenzintervall
für die Varianz
angeben:
wobei
durch
und
durch
bestimmt wird, und deshalb auch
.
Die Grenzen ergeben sich daraus, dass
wie
verteilt ist.
Herleitung der Verteilung der Stichprobenvarianz
Sei
eine Stichprobe von
Messwerten, gezogen aus einer normalverteilten Zufallsvariablen
mit arithmetischem Mittelwert
und Stichprobenvarianz
als Schätzfunktionen
für Erwartungswert
und Varianz
der Grundgesamtheit.
Dann lässt sich zeigen, dass
verteilt ist wie
.
Dazu werden nach Helmert
die
mittels einer orthonormalen
Linearkombination
in neue Variablen
transformiert. Die Transformation lautet:
Die neuen unabhängigen Variablen
sind wie
normalverteilt mit gleicher Varianz
,
aber mit Erwartungswert
beides aufgrund der Faltungsinvarianz
der Normalverteilung.
Außerdem gilt für die Koeffizienten
in
(falls
, ist
)
wegen der Orthonormalität
(Kronecker-Delta) und
damit
Deshalb ergibt sich nun
und schlussendlich nach Division durch
Der Ausdruck auf der linken Seite ist offenbar verteilt wie eine Summe von
quadrierten standardnormalverteilten unabhängigen Variablen mit
Summanden, wie für
gefordert.
Demnach ist also ,
während laut Definition
der Chi-Quadrat-Summe
.
Ein Freiheitsgrad wird hier 'verbraucht', denn im Gegensatz zum Erwartungswert
der Grundgesamtheit
ist der berechnete arithmetische Mittelwert
von den
abhängig.
Beziehung zu anderen Verteilungen
Beziehung zur Gammaverteilung
Die Chi-Quadrat-Verteilung ist ein Spezialfall der Gammaverteilung. Ist
,
so gilt
Beziehung zur Normalverteilung
- Die Summe
von
unabhängigen quadrierten standardnormalverteilten Zufallsvariablen
genügt einer Chi-Quadrat-Verteilung
mit
Freiheitsgraden.
- Für
ist
näherungsweise standardnormalverteilt.
- Für
ist die Zufallsvariable
näherungsweise normalverteilt, mit Erwartungswert
und Standardabweichung
bzw. bei einer nicht-zentralen Chi-Quadrat-Verteilung mit Erwartungswert
und Standardabweichung
.
Beziehung zur Exponentialverteilung
Eine Chi-Quadrat-Verteilung mit 2 Freiheitsgraden ist eine Exponentialverteilung
mit dem Parameter
.
Beziehung zur Erlang-Verteilung
Eine Chi-Quadrat-Verteilung mit
Freiheitsgraden ist identisch mit einer Erlang-Verteilung
mit
Freiheitsgraden und
.
Beziehung zur F -Verteilung
Wenn
und
unabhängige
-verteilte
Zufallsvariablen mit den Freiheitsgraden
und
sind, dann ist der Quotient
eine Zufallsvariable, die der F-Verteilung
mit den Freiheitsgraden
genügt.
Beziehung zur Poisson-Verteilung
Die Verteilungsfunktionen der Poisson-Verteilung
und der -Verteilung
hängen auf folgende Weise zusammen:
Die Wahrscheinlichkeit,
oder mehr Ereignisse in einem Intervall zu finden, innerhalb dessen man im
Mittel
Ereignisse erwartet, gleicht der Wahrscheinlichkeit, dass der Wert von
ist. Es gilt nämlich
mit
und
als regularisierte Gammafunktionen.
Beziehung zur stetigen Gleichverteilung
Für gerade
kann man die
-Verteilung
als
-fache
Faltung bilden mit Hilfe der gleichmäßig
stetigen Dichte
:
,
worin die
unabhängige gleichmäßig stetig verteilte Zufallsvariablen sind.
Für ungerade
gilt dagegen
Herleitung der Dichtefunktion
Die Dichte der Zufallsvariable ,
mit
unabhängig und standardnormalverteilt, ergibt sich aus der gemeinsamen Dichte
der Zufallsvariablen
.
Diese gemeinsame Dichte ist das
-fache
Produkt der Standardnormalverteilungsdichte:
Für die gesuchte Dichte gilt:
mit
Im Grenzwert ist die Summe im Argument der Exponentialfunktion gleich z, sie darf deshalb vor das Integral und den Limes gezogen werden.
Das verbleibende Integral
entspricht dem Volumen der Schale zwischen der Kugel mit Radius
und der Kugel mit Radius
,
wobei
das Volumen der n-dimensionalen
Kugel mit Radius R angibt.
Es folgt:
und nach Einsetzen in den Ausdruck für die gesuchte Dichte:
.
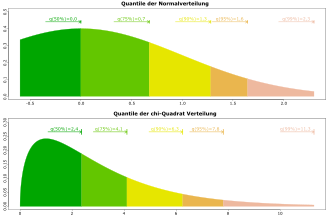
Quantilfunktion
Die Quantilfunktion
der
-Verteilung
ist die Lösung der Gleichung
und damit prinzipiell über die Umkehrfunktion zu berechnen. Konkret gilt
hier
mit >
als Inverse der regularisierten unvollständigen Gammafunktion.
Quantilfunktion für kleinen Stichprobenumfang
Für wenige Werte
(1, 2, 4) kann man die Quantilfunktion auch alternativ angeben:
/DD>
wobei
die Fehlerfunktion,
den unteren Zweig der Lambertschen
W-Funktion bezeichnet und
die Eulersche
Zahl.
Näherung der Quantilfunktion für feste Wahrscheinlichkeiten
Für bestimmte feste Wahrscheinlichkeiten
lassen sich die zugehörigen Quantile
durch die einfache Funktion des Stichprobenumfangs
mit den Parametern
aus der Tabelle annähern, wobei
die Signum
Funktion bezeichnet, die einfach das Vorzeichen ihres Arguments
darstellt:
| 0,005 | 0,01 | 0,025 | 0,05 | 0,1 | 0,5 | 0,9 | 0,95 | 0,975 | 0,99 | 0,995 | |
| -3,643 | -3,298 | -2,787 | -2,34 | -1,83 | 0 | 1,82 | 2,34 | 2,78 | 3,29 | 3,63 | |
| 1,8947 | 1,327 | 0,6 | 0,082 | -0,348 | -0,67 | -0,58 | -0,15 | 0,43 | 1,3 | 2 | |
| -2,14 | -1,46 | -0,69 | -0,24 | 0 | 0,104 | -0,34 | -0,4 | -0,4 | -0,3 | 0 |
Der Vergleich mit einer -Tabelle
zeigt ab
einen relativen Fehler unter 0,4 %, ab
unter 0,1 %. Da die
-Verteilung
für große
in eine Normalverteilung mit Standardabweichung
übergeht,
besitzt der Parameter
aus der Tabelle, der hier frei gefittet
wurde, bei der entsprechenden Wahrscheinlichkeit
etwa die Größe des
-fachen
des Quantils
der Normalverteilung (
),
wobei
die Umkehrfunktion der Fehlerfunktion
bedeutet.
Das 95 % - Konfidenzintervall der Varianz aus dem Abschnitt Beispiel
kann z.B. mit den beiden Funktionen
aus den Zeilen mit
und
auf einfache Weise als Funktion von
grafisch dargestellt werden.
Der Median
befindet sich in der Spalte der Tabelle mit


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 15.11. 2022