Schiefe (Statistik)

Die Schiefe (englischer Fachausdruck: Skewness bzw. Skew) ist eine statistische Kennzahl die die Art und Stärke der Asymmetrie einer Wahrscheinlichkeitsverteilung beschreibt. Sie zeigt an, ob und wie stark die Verteilung nach rechts (positive Schiefe) oder nach links (negative Schiefe) geneigt ist. Jede nicht >symmetrische Verteilung heißt schief.

Definition

Die Schiefe $\operatorname {v} (X)$ einer Zufallsvariablen ist das zentrale Moment 3. Ordnung µ₃(X) (falls das Moment 3. Ordnung existiert), normiert auf die Standardabweichung $\sigma _{X}$ :

$\operatorname {v} (X):={\frac {\mu _{3}(X)}{\sigma ^{3}(X)}}=\operatorname {E} \left[\left({\frac {X-m_{X}}{\sigma _{X}}}\right)^{3}\right]={\frac {\operatorname {E} \left(X^{3}\right)-3\operatorname {Var} (X)\operatorname {E} (X)-\operatorname {E} (X)^{3}}{\operatorname {Var} (X)^{\frac {3}{2}}}}$ .

mit dem Erwartungswert $m_{X}=\operatorname {E} (X)$ . Mit den Kumulanten $\kappa _{i}$ ergibt sich die Darstellung

$\operatorname {v} (X)={\frac {\kappa _{3}}{\sqrt {\kappa _{2}^{3}}}}={\frac {\kappa _{3}}{\operatorname {Var} (X)^{\frac {3}{2}}}}$ .

Die Schiefe kann jeden reellen Wert annehmen.

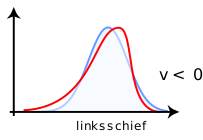
Bei negativer Schiefe, $\operatorname {v} (X)<0$ , spricht man von einer linksschiefen oder rechtssteilen Verteilung; sie fällt in typischen Fällen auf der linken Seite flacher ab als auf der rechten.
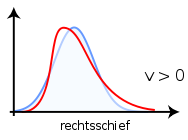
Bei positiver Schiefe, $\operatorname {v} (X)>0$ , spricht man von einer rechtsschiefen oder linkssteilen Verteilung; sie fällt typischerweise umgekehrt auf der rechten Seite flacher ab als auf der linken.

Typische Vertreter rechtsschiefer Verteilungen sind die Bernoulli-Verteilung für $p<1/2$ , die Exponentialverteilung und die Pareto-Verteilung für k>3 .

Die Schiefe ist invariant unter linearer Transformation mit a>0 :

$\operatorname {v} (aX+b)=\operatorname {v} (X)$

Für die Summe unabhängiger normierter Zufallsgrößen $X_{i}$ gilt:

$\operatorname {v} (X_{1}+X_{2}+...+X_{n})=(\operatorname {v} (X_{1})+\operatorname {v} (X_{2})+...+\operatorname {v} (X_{n}))/n^{\frac {3}{2}}$ ,

d.h. die Schiefe der Summe unabhängiger identisch verteiler Zufallsgrößen ist die ursprüngliche Schiefe, dividiert durch ${\sqrt n}$ .

Empirische Schiefe

Zur Berechnung der Schiefe einer empirischen Häufigkeitsverteilung wird die folgende Formel benutzt:

$v={\frac {1}{n}}\sum _{i=1}^{n}\left({\frac {x_{i}-{\bar {x}}}{s}}\right)^{3}$

Damit die Schiefe unabhängig von der Maßeinheit der Variablen ist, werden die Messwerte mit Hilfe des arithmetischen Mittelwertes ${\bar {x}}$ und der Standardabweichung der Beobachtungswerte $x_{i}$

$z_{i}={\frac {x_{i}-{\bar {x}}}{s}}$

standardisiert. Durch die Standardisierung gilt

${\bar {z}}={\frac {1}{n}}\sum _{i=1}^{n}z_{i}=0$ und $s_{z}={\frac {1}{n}}\sum _{i=1}^{n}z_{i}^{2}=1$ .

Schätzung der Schiefe einer Grundgesamtheit

Zur Schätzung der unbekannten Schiefe $\nu$ einer Grundgesamtheit mittels Stichprobendaten $x_{1},\ldots ,x_{n}$ ( der Stichprobenumfang) müssen der Erwartungswert und die Varianz aus der Stichprobe geschätzt werden, d.h. die theoretischen durch die empirischen Momente ersetzt werden:

${\hat {\nu }}={\frac {1}{n}}\sum _{i=1}^{n}\left({\frac {x_{i}-{\bar {x}}}{s}}\right)^{3}$

mit ${\bar {x}}$ der Stichprobenmittelwert und die Stichprobenstandardabweichung. Dieser Schätzer ist jedoch nicht erwartungstreu im Gegensatz zu

${\hat {\nu }}'={\frac {n}{(n-1)(n-2)}}\sum _{i=1}^{n}\left({\frac {x_{i}-{\bar {x}}}{s}}\right)^{3}$ .

Weitere Schiefemaße

Lage von Mittelwert und Median

Auf Karl Pearson geht die Definition

$S={\frac {\mu -x_{0.5}}{\sigma }}$

mit dem Erwartungswert µ, dem Median $x_{0.5}$ und der Standardabweichung σ zurück. Der Wertebereich von S ist das Intervall [-1,1]. Für symmetrische Verteilungen ist S = 0. Rechtsschiefe Verteilungen besitzen häufig ein positives S, es gibt jedoch Ausnahmen von dieser Faustregel.

Wenn die Standardabweichung divergiert, kann die Pearsonsche Definition verallgemeinert werden, indem ein Verteilung rechtsschief bezeichnet wird, wenn der Median kleiner als der Erwartungswert ist. In diesem Sinn ist die Pareto-Verteilung für beliebigen Parameter k>1 rechtsschief.

Quantilskoeffizient der Schiefe

Der Quantilskoeffizient der Schiefe beschreibt die normierte Differenz zwischen der Entfernung des $\alpha-$ und des $(1-\alpha)$ -Quantils zum Median. Er wird also wie folgt berechnet:

$QS = \frac{(x_{1-\alpha} - x_{0.5}) - ({x_{0.5} - x_{\alpha}})}{x_{1-\alpha} - x_{\alpha}}$ , $\alpha\in (0,0.5)$

Dabei kann der Quantilskoeffizient Werte zwischen -1 und 1 annehmen. Der Quantilskoeffizient existiert für beliebige Verteilungen, auch wenn Erwartungswert oder die Standardabweichung nicht definiert sein sollten.

Eine symmetrische Verteilung besitzt den Quantilskoeffizienten 0; eine rechtsschiefe (linksschiefe) Verteilung besitzt in der Regel einen positiven (negativen) Quantilskoeffizienten. Für $\alpha=0.25$ ergibt sich der Quartilskoeffizient. Die Pareto-Verteilung besitzt für beliebige Parameter k>0 positive Quantilskoeffizienten.

Deutung

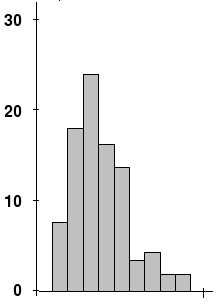
Beispiel von experimentellen Daten mit einer positiven Schiefe

Ist $\operatorname{v}>0$ , so ist die Verteilung rechtsschief, ist $\operatorname{v}<0$ , ist die Verteilung linksschief. Bei rechtsschiefen Verteilungen sind Werte, die kleiner sind als der Mittelwert, häufiger zu beobachten, so dass sich der Gipfel (Modus) links vom Mittelwert befindet; der rechte Teil des Graphs ist flacher als der linke. Gilt $\operatorname{v}=0$ , so ist die Verteilung auf beiden Seiten ausgeglichen. Bei symmetrischen Verteilungen ist immer $\operatorname{v}=0$ . Umgekehrt müssen Verteilungen mit $\operatorname{v}=0$ nicht symmetrisch sein.

Als Daumenregeln kann man also festhalten:

rechtsschief: $x_{{\text{mod}}}<x_{{\text{med}}}<\overline {x}$
symmetrisch: $x_{{\text{mod}}}=x_{{\text{med}}}=\overline {x}$
linksschief: $x_{{\text{mod}}}>x_{{\text{med}}}>\overline {x}$

Die Schiefe ist ein Maß für die Asymmetrie einer Wahrscheinlichkeitsverteilung. Da die Gaußsche Normalverteilung symmetrisch ist, d.h. eine Schiefe von null besitzt, ist die Schiefe eine mögliche Maßzahl, um eine Verteilung mit der Normalverteilung zu vergleichen.

Interpretation der Schiefe

Rechtsschiefe Verteilungen findet man z.B. häufig beim Pro-Kopf-Einkommen. Hier gibt es einige wenige Personen mit extrem hohem Einkommen und sehr viele Personen mit eher niedrigem Einkommen. Durch die 3. Potenz erhalten die wenigen sehr extremen Werte ein hohes Gewicht und es entsteht ein Schiefemaß mit positivem Vorzeichen. Es gibt verschiedene Formeln, um die Schiefe zu berechnen. Die gängigen Statistikpakete wie SPSS, SYSTAT, Stata etc. nutzen besonders im Falle einer kleinen Fallzahl von obiger, momentbasierter Berechnungsvorschrift abweichende Formeln.

Siehe auch

Wölbung (Statistik)

Basierend auf einem Artikel in:

Wikipedia.de