Bernoulli-Verteilung

Wahrscheinlichkeitsfunktion der Bernoulli-Verteilung für

(blau),

(grün) und

(rot)

Zufallsgrößen mit einer Bernoulli-Verteilung (auch als Null-Eins-Verteilung, Alternativ-Verteilung oder Boole-Verteilung bezeichnet) benutzt man zur Beschreibung von zufälligen Ereignissen, bei denen es nur zwei mögliche Versuchsausgänge gibt. Einer der Versuchsausgänge wird meistens mit Erfolg bezeichnet und der komplementäre Versuchsausgang mit Misserfolg. Die zugehörige Wahrscheinlichkeit für einen Erfolg nennt man Erfolgswahrscheinlichkeit und q=1-p die Wahrscheinlichkeit eines Misserfolgs. Beispiele:

Werfen einer Münze: Kopf (Erfolg), , und Zahl (Misserfolg), .
Werfen eines Würfels, wobei nur eine „6“ als Erfolg gewertet wird: ,
Qualitätsprüfung (einwandfrei, nicht einwandfrei).
Anlagenprüfung (funktioniert, funktioniert nicht).
Betrachte sehr kleines Raum/Zeit-Intervall: Ereignis tritt ein $(p\gtrapprox 0)$ , tritt nicht ein $(q\lessapprox 1)$ .

Die Bezeichnung Bernoulli-Versuch (Bernoullian trials nach Jakob I. Bernoulli) wurde erstmals 1937 in dem Buch Introduction to Mathematical Probability von James Victor Uspensky verwendet.

Definition

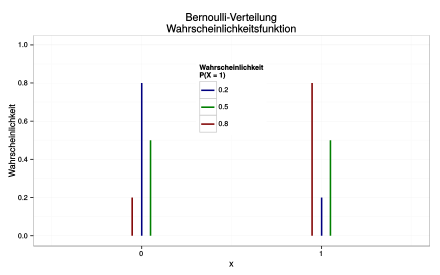
Eine diskrete Zufallsgröße mit Werten in der Menge $\{0,1\}$ unterliegt der Null-Eins-Verteilung bzw. Bernoulli-Verteilung mit dem Parameter $p\in \,]0,1[$ , wenn sie die folgenden Einzelwahrscheinlichkeiten besitzt.

$\operatorname {P}(X=1)=p$ und $\operatorname {P}(X=0)=q=1-p$ .

Die Verteilungsfunktion ist dann

$F_{X}(x)={\begin{cases}0&{\text{ falls }}x<0\\1-p&{\text{ falls }}0\leq x<1\\1&{\text{ falls }}x\geq 1\end{cases}}$

Man schreibt dann $X\sim B(p)$ oder $X\sim Ber_{p}$ .

Eine Reihe von unabhängigen identischen Versuchen, bei der jeder Einzelversuch der Bernoulli-Verteilung genügt, wird Bernoulli-Prozess oder bernoullisches Versuchsschema genannt.

Eigenschaften

Erwartungswert

Die Bernoulli-Verteilung mit Parameter hat den Erwartungswert:

$\operatorname {E}\left(X\right)=p$

Dies hat den Grund, dass für eine Bernoulli verteilte Zufallsvariable mit P(X=1)=p und P(X=0)=q gilt

$\operatorname{E}(X) = P(X=1)\cdot 1 + P(X=0)\cdot 0 = p \cdot 1 + q\cdot 0 = p$

Varianz und weitere Streumaße

Die Bernoulli-Verteilung besitzt die Varianz

$\operatorname {Var} (X)=p\cdot (1-p)=pq$

denn es ist $E(X^2)=p\cdot 1^2+ q\cdot 0^2=p$ und damit

$\operatorname {E}\left(X^{2}\right)-\operatorname {E}(X)^{2}=p-p^{2}=p\cdot (1-p)=pq$

Damit ist die Standardabweichung

$\sigma _{X}={\sqrt {pq}}$

und der Variationskoeffizient

$\operatorname {VarK}(X)={\sqrt {{\frac {q}{p}}}}$

Symmetrie

Für den Parameter $p={\tfrac {1}{2}}$ ist die Bernoulli-Verteilung symmetrisch um den Punkt $a={\tfrac {1}{2}}$ .

Schiefe

Die Schiefe der Bernoulli-Verteilung ist

$\operatorname {v}(X)={\frac {1-2p}{{\sqrt {pq}}}}$

Dies kann folgendermaßen gezeigt werden. Eine standardisierte Zufallsvariable $\frac{X-\operatorname{E}(X)}{\sqrt{\operatorname{Var}(X)}}$ mit Bernoulli-verteilt nimmt den Wert $\frac{q}{\sqrt{pq}}$ mit Wahrscheinlichkeit an und den Wert $-\frac{p}{\sqrt{pq}}$ mit Wahrscheinlichkeit . Damit erhalten wir für die Schiefe

${\begin{aligned}\operatorname {v} (X)&=\operatorname {E} \left[\left({\frac {X-\operatorname {E} (X)}{\sqrt {\operatorname {Var} (X)}}}\right)^{3}\right]\\&=p\cdot \left({\frac {q}{\sqrt {pq}}}\right)^{3}+q\cdot \left(-{\frac {p}{\sqrt {pq}}}\right)^{3}\\&={\frac {1}{{\sqrt {pq}}^{3}}}\left(pq^{3}-qp^{3}\right)\\&={\frac {pq}{{\sqrt {pq}}^{3}}}(q-p)\\&={\frac {q-p}{\sqrt {pq}}}\end{aligned}}$

Wölbung und Exzess

Der Exzess der Bernoulli-Verteilung ist

$\gamma (X)={\frac {1-6pq}{pq}}$

und damit ist die Wölbung

$\beta _{2}(X)={\frac {1-3pq}{pq}}$

Momente

Alle k-ten Momente $m_{k}$ sind gleich und es gilt

$m_{k}=p$ .

Es ist nämlich

$m_{k}=E\left(X^{k}\right)=p\cdot 1^{k}+q\cdot 0^{k}=p$ .

Entropie

Die Entropie der Bernoulli-Verteilung ist

$\mathrm{H} =-q\log _{2}(q)-p\log _{2}(p)$

gemessen in Bit.

Modus

Der Modus der Bernoulli-Verteilung ist

$x_{D}={\begin{cases}0&{\text{falls }}q>p\\0;1&{\text{falls }}q=p\\1&{\text{falls }}q<p\end{cases}}$ .

Median

Der Median der Bernoulli-Verteilung ist

${\tilde {m}}_{X}={\begin{cases}0&{\text{falls }}q>p,\\1&{\text{falls }}q<p,\end{cases}}$

falls $p=q$ gilt, ist jedes ${\tilde {m}}_{X}\in [0,1]$ ein Median.

Kumulanten

Die kumulantenerzeugende Funktion ist

$g_{X}(t)=\ln(pe^{t}+q)$ .

Damit sind die ersten Kumulanten $\kappa _{1}=p,\kappa _{2}=pq$ und es gilt die Rekursionsgleichung

$\kappa _{{n+1}}=p(1-p){\frac {d\kappa _{n}}{dp}}.$

Wahrscheinlichkeitserzeugende Funktion

Die wahrscheinlichkeitserzeugende Funktion ist

$m_{X}(t)=1-p+pt$

Charakteristische Funktion

Die charakteristische Funktion ist

$\varphi _{X}(t)=1-p+pe^{{{\mathrm {i}}t}}$ .

Momenterzeugende Funktion

Die momenterzeugende Funktion ist

Beziehung zu anderen Verteilungen

Beziehung zur Binomialverteilung

Die Bernoulli-Verteilung ist ein Spezialfall der Binomialverteilung für n=1 . Mit anderen Worten, die Summe von unabhängigen Bernoulli-verteilten Zufallsgrößen mit identischem Parameter genügt der Binomialverteilung, demnach ist die Bernoulli-Verteilung nicht reproduktiv. Die Binomialverteilung ist die -fache Faltung der Bernoulli-Verteilung bei gleichem Parameter bzw. mit gleicher Wahrscheinlichkeit .

Beziehung zur verallgemeinerten Binomialverteilung

Die Summe von voneinander unabhängigen Bernoulli-verteilten Zufallsvariablen, die alle einen unterschiedlichen Parameter $p_{i}$ besitzen, ist verallgemeinert binomialverteilt.

Beziehung zur Poisson-Verteilung

Die Summe von Bernoulli-verteilten Zufallsgrößen genügt für $n\to \infty$ , $p_{{n}}\to 0$ und $\lim \limits _{{n\to \infty }}np_{{n}}=\lambda >0$ einer Poisson-Verteilung mit dem Parameter $\lambda$ . Dies folgt direkt daraus, dass die Summe binomialverteilt ist und für die Binomialverteilung die Poisson-Approximation gilt.

Beziehung zur Zweipunktverteilung

Die Bernoulli-Verteilung ist ein Spezialfall der Zweipunktverteilung mit a=0,b=1 . Umgekehrt ist die Zweipunktverteilung eine Verallgemeinerung der Bernoulli-Verteilung auf beliebige zweielementige Punktmengen.

Beziehung zur Rademacher-Verteilung

Sowohl die Bernoulli-Verteilung mit p=q=0{,}5 als auch die Rademacher-Verteilung modellieren einen fairen Münzwurf (oder eine faire, zufällige Ja/Nein-Entscheidung). Der Unterschied besteht lediglich darin, dass Kopf (Erfolg) und Zahl (Misserfolg) unterschiedlich codiert werden.

Beziehung zur geometrischen Verteilung

Bei Hintereinanderausführung von Bernoulli-verteilten Experimenten ist die Wartezeit auf den ersten Erfolg (oder letzten Misserfolg, je nach Definition) geometrisch verteilt.

Beziehung zur diskreten Gleichverteilung

Die Bernoulli-Verteilung mit $p=q={\frac {1}{2}}$ ist eine diskrete Gleichverteilung auf $\{0,1\}$

Urnenmodell

Die Bernoulli-Verteilung lässt sich auch aus dem Urnenmodell erzeugen, wenn $p={\frac {p_{1}}{p_{2}}}\in {\mathbb {Q}}$ ist. Dann entspricht dies dem einmaligen Ziehen aus einer Urne mit $p_{2}$ Kugeln, von denen genau $p_{1}$ rot sind und alle anderen eine andere Farbe besitzen. Die Wahrscheinlichkeit, eine rote Kugel zu ziehen, ist dann Bernoulli-verteilt.

Simulation

Bei der Simulation macht man sich zunutze, dass wenn ${\mathcal {U}}$ eine stetig gleichverteilte Zufallsvariable auf [0,1] ist, die Zufallsvariable $Y={\mathbf {1}}_{{\{{\mathcal {U}}\geq 1-p\}}}$ Bernoulli-verteilt ist mit Parameter . Da fast jeder Computer Standardzufallszahlen erzeugen kann, ist die Simulation wie folgend:

Erzeuge eine Standardzufallszahl $u_{i}$
Ist $u_{i}\leq 1-p$ , gib 0 aus, ansonsten gib 1 aus.

Dies entspricht genau der Inversionsmethode. Die einfache Simulierbarkeit von Bernoulli-verteilten Zufallsvariablen kann auch zur Simulation von binomialverteilten oder verallgemeinert Binomialverteilten Zufallsvariablen genutzt werden.

Basierend auf einem Artikel in:

Wikipedia.de