Inversionsmethode

Inversionsmethode.

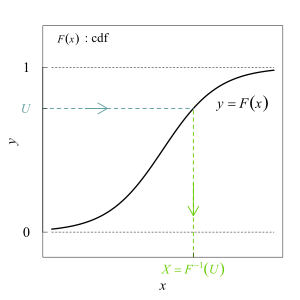
Die Inversionsmethode ist ein Simulationsverfahren, um aus gleichverteilten Zufallszahlen andere Wahrscheinlichkeitsverteilungen zu erzeugen.

Intention

Die Erzeugung dieser Zufallszahlen wird durch künstlich herbeigeführte Realisierungen einer statistischen Zufallsvariablen nachgestellt. Man kann Zufallszahlen verschiedener diskreter und stetiger Wahrscheinlichkeitsverteilungen erzeugen. Diese Folgen von Zufallszahlen werden beispielsweise verwendet, um das Verhalten komplexer Systeme, die man nur unter Schwierigkeiten mit mathematischen Funktionen analysieren kann, zu untersuchen. Beispiele wären die Warteschlangentheorie oder die Verteilung von bestimmten Stichprobenfunktionen, etwa der nichtzentralen Betaverteilung.

Die Basis für die Erzeugung der Zufallszahl einer bestimmten Verteilung F(x) ist in der Regel eine Rechteckverteilung oder Gleichverteilung im Intervall [0,1] . Ausgehend davon, dass auch die Verteilungsfunktion einen Bildbereich zwischen Null und Eins aufweist, wählt man nun in diesem Intervall zufällig eine Zahl, die man als Wert der gewählten Wahrscheinlichkeitsverteilung F(x) interpretiert und damit den dazugehörigen Wert der Zufallsvariablen selbst, ihr sogenanntes Quantil, als die letztlich gesuchte Zufallszahl findet (die diese Zahl liefernde Quantilfunktion ist dabei also nichts anderes als die Umkehrfunktion der entsprechenden Verteilungsfunktion).

Simulationslemma

Formulierung

Definition von $F^{{-1}}(y)$ .

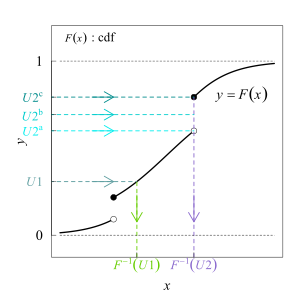
Die Inversionsmethode basiert auf dem Simulationslemma, einem Lemma, das besagt, dass man aus einer gleichverteilten Zufallsvariablen eine Zufallsvariable mit einer anderen Verteilungsfunktion erzeugen kann.

Sei F(x) eine Verteilungsfunktion und eine Wahrscheinlichkeit (also eine Zahl aus dem Intervall [0,1] ). Das -Quantil beziehungsweise die Quantilfunktion der Verteilungsfunktion ist definiert als

$F^{{-1}}(p):=\inf \left\{x\in {\mathbb {R}}\mid F(x)\geq p\right\}$ .

Falls für p=1 die Menge auf der rechten Seite leer und das Infimum nicht definiert ist, setzt man $F^{{-1}}(1):=\infty$ .

Sei nun eine auf dem Intervall [0,1] gleichverteilte Zufallsvariable.

Dann ist $X:=F^{{-1}}(U)$ eine reelle Zufallsvariable, die der Verteilungsfunktion genügt.

Die Quantilfunktion $F^{{-1}}$ wird benötigt, um auch den Fall einer nicht injektiven Verteilungsfunktion, etwa der einer diskreten Zufallsvariablen, mit abzudecken. Ist die Verteilungsfunktion streng monoton steigend, kann die gewöhnliche Umkehrfunktion der Verteilung verwendet werden.

Beweis

Zwar ist $F^{{-1}}$ nicht im strengen Sinne eine Umkehrabbildung zu , aber dennoch gilt wenigstens

$F^{{-1}}(U)\leq x\iff U\leq F(x)$

wegen der rechtsseitigen Stetigkeit von . Damit gilt aber

${\mathbb {P}}(X\leq x)={\mathbb {P}}\left(F^{{-1}}(U)\leq x\right)={\mathbb {P}}\left(U\leq F(x)\right)=F(x)$ .

Der letzte Schritt ist korrekt, da laut Annahme eine stetig gleichverteilte Zufallszahl auf dem Intervall [0,1] ist und daher ${\mathbb {P}}(U\leq y)=y$ für alle $y\in [0,1]$ gilt.

Fazit

Viele Verteilungsfunktionen lassen sich unter Ausnutzung des Simulationslemmas aus gleichverteilten Zufallszahlen erzeugen. Allerdings ist es zu vielen Verteilungsfunktionen in der Praxis nicht möglich, mit vertretbarem Aufwand die Quantilfunktion zu bestimmen.

Anwendung bei diskreter Verteilung

Zugrunde liegen den Beispielen Zufallszahlen aus dem Intervall [0,1] .

Beispiel einer Verteilung mit zwei Werten

Zufallszahlen F(x) bestimmen x und damit die Häufigkeiten von P(1) und P(2).

In einer Porzellanfabrik werden Kaffeekannen hergestellt. Die Henkel und Schnäbel der Kannen werden vor dem Brennen von Hand angeklebt. Erfahrungsgemäß sind 25 % der Teile nicht ordnungsgemäß befestigt. Nach dem Brennen werden die Kannen nacheinander geprüft.

Ist die Kanne in Ordnung, wird eine Eins vergeben: Das ist in 75 % aller Kannen der Fall.

Ist sie zu beanstanden, vergibt der Prüfer eine Zwei: Das kommt bei 25 % aller Kannen vor.

Wir wollen nun eine Folge von Kannen simulieren:

Definieren wir die obige Vorgabe als Verteilung einer Zufallsvariablen :

Für alle anderen Werte von ist .

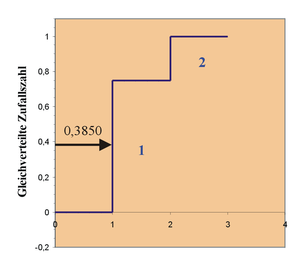
Man könnte nun so vorgehen: Es wird eine Zufallszahl ( =F(X) ) im Intervall [0,1] erzeugt. Liegt zwischen 0 und 0,75, bekommt die Zufallszahl den Wert 1, sonst den Wert 2. Auf diese Weise erzeugen wir 75 % Einsen und 25 % Zweien. Es ergibt sich also beispielsweise in der Tabelle unten eine Folge von (1;2)-Zufallszahlen. Die Grafik verdeutlicht den Vorgang der Zuordnung anhand des ersten Wertes. Die Gleichverteilung produzierte ein y=0{,}3850 . Hier wird x=1 vergeben.

A: Nr. der Kanne
B: Gleichverteilte Zufallszahl	
C: Zustand der Kanne
A      B         C
1      0,39      1
2      0,34      1
3      0,41      1
4      0,93      2
5      0,05      1
6      0,44      1
7      0,95      2
8      0,43      1
9      0,07      1
10     0,77      2
11     0,02      1
12     0,93      2
13     0,68      1
14     0,26      1
15     0,94      2
16     0,88      2
17     0,23      1
18     0,91      2
19     0,51      1
20     0,69      1

Beispiel Poisson-verteilter Zufallszahlen

Die Zufallszahlen werden als F(x) interpretiert und liefern Poisson-verteilte x-Werte.

Um den Kundenservice zu optimieren, wird die Zahl der Kunden erfasst, die innerhalb einer Minute an einen bestimmten Bankschalter kommen. Man weiß aus Erfahrung, dass pro Minute im Durchschnitt 1,2 Kunden an den Schalter kommen. Die Zahl der ankommenden Kunden soll simuliert werden. Eine gute Näherung für die Verteilung ist die Poisson-Verteilung mit dem Parameter $\lambda =1{,}2$ Kunden/Minute. Ihre Werte für diesen Fall lauten:

x:    Zahl der Kunden in einer Minute
f(x): Wahrscheinlichkeit für genau     x Kunden
F(x): Wahrscheinlichkeit für höchstens x Kunden 
---
x      f(x)      F(x)
0      0,3       0,3
1      0,36      0,66
2      0,22      0,88
3      0,09      0,97
4      0,03      0,99
5      ca.0      ca. 1

Analog zu oben verwenden wir hier wieder die Verteilung F(x) für die Simulation.

A: Minuten-Index:
B: Gleichverteilte Zufallszahl: F(x)
C: Zahl der neu hinzu kommenden Kunden: 1,2 Kunden / Minute: x
D: Zahl der verbleibenden Kunden nach Bedienung von 1,5 Kunden / Minute (siehe unten)
E: Wie D, gerundet auf ganze Zahlen (siehe unten)
----
A	B	C	D	E
1	0,63	1	0	0
2	0,55	1	0	0
3	0,21	0	0	0
4	0,93	3	1,5	2
5	0,85	2	2	2
6	0,96	3	3,5	4
7	0,81	2	4	4
8	0,68	2	4,5	5
9	0,88	2	5	5
10	0,04	0	3,5	4
11	0,51	1	3	3
12	0,07	0	1,5	2
13	0,28	0	0	0
14	0,59	1	0	0
15	0,55	1	0	0
16	0,68	2	0,5	1
17	0,61	1	0	0
18	0,08	0	0	0
19	0,57	1	0	0
20	0,56	1	0	0
21	0,52	1	0	0
22	0,1 	0	0	0
23	0,27	0	0	0
24	0,17	0	0	0
25	0,72	2	0,5	1
26	0,06	0	0	0
27	0,55	1	0	0
28	0,92	3	1,5	2
29	0,72	2	2	2
30	0,03	0	0,5	1

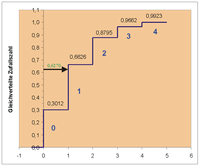
In der ersten Minute liegt die gleichverteilte Zufallszahl y=0{,}6270 zwischen 0,3012 und 0,6626, wie in der Grafik angedeutet. Hier erhält den Wert 1.

In der zweiten Minute liegt y=0{,}5508 wieder zwischen 0,3012 und 0,6626, erhält wieder den Wert 1 usw.

Es ergibt also die Folge der ankommenden Kunden wie in der Tabelle.

Man könnte nun mit der Simulation untersuchen, ob die Schlange der Kunden sehr groß werden kann, ob man beispielsweise einen weiteren Schalter offenhalten sollte.

Exkurs in die Warteschlangentheorie

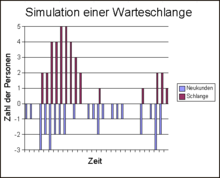
Unten kommende Neukunden, oben wartende Kunden.

In einer sehr vereinfachten Systemsimulation wird die entstehende Warteschlange der Bankkunden untersucht: Im Mittel kommen, wie im Beispiel oben, 1,2 Kunden pro Minute. Bedient werden sollen im Durchschnitt 1,5 Kunden pro Minute. Man könnte vermuten, dass es keine Warteschlangen gibt, weil ja im Mittel mehr Kunden bedient werden als ankommen. Eine Simulation mit der Poisson-Verteilung ergibt aber folgendes Bild:

Es haben sich in einer knappen Stunde Schlangen mit bis zu fünf Personen gebildet. Die Ursache liegt darin, dass die Bearbeitungskapazität in den Zeiträumen nicht genutzt wird, wenn keine Kunden anwesend sind (es gibt keine negativen Kundenzahlen).

Anwendung bei stetiger Verteilung

Für die Verteilung einer stetigen Zufallsvariablen ergibt sich statt einer Treppenfunktion eine stetige, streng monoton steigende Verteilungskurve.

Beispiel einer Gleichverteilung

Gleichverteilte Zufallszahlen aus dem Intervall [0,1] werden für die Simulation eines Random Walk herangezogen. Es gilt dann für die stetige Gleichverteilung auf den Intervall $[-{\tfrac {1}{2}},{\tfrac {1}{2}}]$ : $F^{-1}(x)=x-{\tfrac {1}{2}}$ .

Anschaulich: Die Zufallszahlen werden um 0,5 vermindert, d.h. $[0,1]\to [-{\tfrac {1}{2}},{\tfrac {1}{2}}]$ . Die Zahlen werden als Schrittlängen interpretiert, die je nach Vorzeichen vorwärts oder rückwärts gesetzt werden.

Beispiel für Exponentialverteilung

Exponential-Verteilungsfunktion

Die Verteilungsfunktion etwa der Exponentialverteilung ist

$F(x)=1-e^{{-\lambda x}}.$

Als Umkehrfunktion erhalten wir dann

$x=F^{{-1}}(y)=-{\frac {1}{\lambda }}\ln(1-y).$

Die Zeit, die zwischen zwei Anfragen an einen bestimmten Wikipedia-Server liegt, sei exponentialverteilt mit dem Parameter $\lambda =2{\mbox{ Zugriffe/Zeiteinheit}}$ . Es sollen die Zeiten x simuliert werden, die zwischen zwei Anfragen an den Server liegen. Den Beispielen zugrunde liegen Zufallszahlen aus dem Intervall [0,1] .

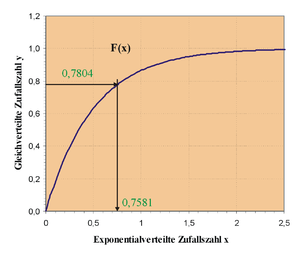
Die Verteilungsfunktion

$F(x)=1-e^{{-\lambda \cdot x}}$

ist in der Grafik rechts dargestellt. Der Ordinatenwert F(x) entspricht der Zufallszahl , der entsprechende Abszissenwert ist die gesuchte exponentialverteilte Zufallszahl.

Rechnerisch einfacher ist es, mit der Umkehrfunktion $F^{{-1}}(y)$ zu arbeiten und zu berücksichtigen, dass sich an den Zufallszahlen aus dem Intervall [0,1] nichts ändert, wenn wir (1-y) durch ersetzen:

$x=F^{{-1}}(y)=-{\frac {\ln(y)}{\lambda }}$

In der Tabelle-1 ist eine Folge von exponentialverteilten Zufallszahlen dargestellt. Die Grafik unten gibt diese Zahlen als Zeitreihe wieder.

Tabelle-1
lambda = 2 Zugriffe / Zeiteinheit
A: Index
B: exponentialverteilte Zufallszahl
C: B aufsummiert = Zeitpunkte des Eintreffens
---
A        B      C             
0	 0,00	0,00
1	 0,58	0,58	
2	 1,17	1,76	
3	 0,31	2,07	
4	 0,02	2,09		
5	 0,25	2,34		
6	 1,58	3,92	
7	 0,15	4,07	
8	 0,25	4,32			     
9	 0,06	4,38
10	 0,17	4,55
11	 0,21	4,76
12	 0,20	4,96
13	 0,70	5,66
14	 0,22	5,88
15	 0,17	6,05
16	 0,42	6,47
17	 0,00	6,47
18	 1,89	8,36
19	 0,40	8,76
20	 0,76	9,52
21	 0,37	9,88
22	 0,53	10,42
23	 0,54	10,96
24	 0,36	11,32
25	 0,41	11,73
26	 0,38	12,11
27	 1,31	13,42
28	 0,13	13,55
29	 0,05	13,61
30	 1,95	15,55
31	 1,60	17,15
32	 0,35	17,50
33	 0,81	18,31
34	 0,29	18,60
35	 0,32	18,92
36	 0,30	19,22
37	 1,43	20,65
38	 0,55	21,20
39	 0,01	21,21
40	 0,33	21,54
41	 0,48	22,03
42	 1,13	23,16
43	 0,97	24,13
44	 0,42	24,54
Mittelwert von B: 0,56 (berechnet: 1/lambda = 0,5)
Standardabweichung von B: 0,51 (berechnet: 0,5)

Zeitliche Abfolge der Zugriffe auf einen Server bei einem Mittelwert von 2 Zugr./Zeiteinheit.

Während die zeitliche Abfolge der Zugriffe exponentialverteilt ist, folgt die Zahl der Zugriffe pro Zeiteinheit einer Poisson-Verteilung. Beispielsweise werden 4 Intervalle beobachtet, innerhalb derer kein Ereignis auftritt und 8 Intervalle mit einem Ereignis, siehe Tabelle-2. Für die beiden Fälle macht die Poisson-Verteilung die Vorhersagen von 3,1 bzw. 6,2 -- in Anbetracht der geringen Anzahl der Werte eine gute Übereinstimmung.

Tabelle-2
A: Zahl der Ereignisse pro Intervall, basierend auf C in Tabelle-1
B: Gemessene Ereignisse 
C: Berechneter Wert für E nach Poisson-Verteilung
---
A	B	C
0	4	3,11
1	8	6,23
2	5	6,23
3	4	4,15
4	2	2,08
5	1	0,83
6	0	0,28

Weitere Beispiele

Hier sind einige Beispiele aufgelistet, wie sich aus einer gleichverteilten Zufallsvariable mit $F^{{-1}}$ gegebene Verteilungen bzw. erzeugen lassen.

Dichtefunktion	Verteilungsfunktion	Quantilfunktion	Bereich
$f(x)=x\cdot {\mathrm {const.}}$	$F(x)=x^{2}\cdot {\mathrm {const.}}$	$F^{{-1}}(U)=a\cdot {\sqrt {U}}$	$0\leq U\leq 1,\quad 0\leq x\leq a$
$f(x)=x^{n}\cdot {\mathrm {const.}}$	$F(x)=x^{{n+1}}\cdot {\mathrm {const.}}$	$F^{{-1}}(U)=a\cdot {\sqrt[ {n+1}]{U}}$	$0\leq U\leq 1,\quad 0<x\leq a,\quad n>-1$
$f(x)={\frac {{\mathrm {const.}}}{x^{n}}}$	$F(x)={\frac {{\mathrm {const.}}}{x^{{n-1}}}}$	$F^{{-1}}(U)={\frac {a}{{\sqrt[ {n-1}]{U}}}}$	> $0<U\leq 1,\quad a\leq x<\infty ,\quad n>1$
$f(x)=e^{{-\lambda x}}\cdot \lambda$	$F(x)=1-e^{{-\lambda x}}$	$F^{{-1}}(U)=-{\frac {1}{\lambda }}\ln(U)$	$0<U\leq 1,\quad 0\leq x<\infty$
$f(x)=\sin(x)$	$F(x)=1-\cos(x)$	$F^{{-1}}(U)=\arccos(U)$	$0\leq U\leq 1,\quad 0\leq x\leq \pi /2$
$f(x)=\cos(x)$	$F(x)=\sin(x)$	$F^{{-1}}(U)=\arcsin(U)$	$0\leq U\leq 1,\quad 0\leq x\leq \pi /2$
$f(x)={\frac {1}{\pi (1+x^{2})}}$	$F(x)={\frac 12}+{\frac 1\pi }\arctan(x)$	$F^{{-1}}(U)=-\cot(\pi U)$	$0<U<1,\quad -\infty <x<\infty$

Probleme

Nicht immer lässt sich die im Simulationslemma benutzte Quantilfunktion bestimmen. Dann lässt sich die Inversionsmethode nicht anwenden. Als Lösung bietet sich in solchen Fällen häufig die Verwerfungsmethode an.

Normalverteilung

Da für die Normalverteilung die Inverse nicht unmittelbar ermittelt werden kann, bleibt auch für sie das Simulationslemma eine theoretische Idee.

Verschiedene Ansätze zur Erzeugung normalverteilter Zufallszahlen sind im Artikel Normalverteilung, Abschnitt Erzeugung normalverteilter Zufallszahlen zusammengefasst.

Bei der Erzeugung von multivariaten normalverteilten Zufallszahlen müssen die erzeugten stochastisch unabhängigen Zufallszahlen noch korreliert werden. Man erreicht das, indem die Datenmatrix der unabhängigen Zufallszahlen mit S^1/2 multipliziert wird. Hierbei bezeichnet S^1/2 die Cholesky-Zerlegung von S und S die Kovarianzmatrix der zu simulierenden Normalverteilung.

Literatur

Michael Kolonko: Stochastische Simulation: Grundlagen, Algorithmen und Anwendungen. Vieweg+Teubner, Wiesbaden 2008, ISBN 978-3-8351-0217-0.

Basierend auf einem Artikel in:

Wikipedia.de