Verwerfungsmethode

Die Verwerfungsmethode (auch Acceptance-Rejection-Verfahren; engl. rejection sampling) ist eine Methode zur Erzeugung von Zufallszahlen zu einer vorgegebenen Verteilung und geht auf John von Neumann zurück. Sie kann genutzt werden, wenn die Inversion der Verteilungsfunktion nicht möglich oder zu aufwendig ist.

Idee

$F\,$ sei hierbei die Verteilungsfunktion der Verteilung, zu der Zufallszahlen erzeugt werden sollen. $G\,$ sei eine Hilfsverteilungsfunktion, zu der sich auf einfachem Weg – etwa über die Inversionsmethode – Zufallszahlen erzeugen lassen. Es seien ferner $f\,$ und $g\,$ die zugehörigen Dichten.

Um die Verwerfungsmethode anwenden zu können, muss zudem ein konstantes $k\in {\mathbb {R}}$ existieren, so dass $f(x)\leq k\cdot g(x)$ für jedes $x\in \mathbb {R}$ erfüllt ist. Das wird benötigt, da die Fläche unter einer Dichtefunktion immer 1 ist. Ohne den Vorfaktor gäbe es deshalb zwangsläufig Stellen mit f(x)>g(x) .

Seien nun $u_{i}\,$ Standardzufallszahlen und $v_{i}\,$ Zufallszahlen, die der Verteilungsfunktion $G\,$ genügen.

Dann genügt mit $j:=\inf\{n\geq 1\mid k\cdot u_{n}\cdot g(v_{n})<f(v_{n})\}$ die Zufallszahl $x:=v_{j}$ der Verteilungsfunktion . Man wartet gewissermaßen auf einen ersten Treffer, der unterhalb von liegt.

Anders gesagt: Es werden Zufallszahlen $v_{i}$ nach der Verteilungsfunktion erzeugt, und die Zahl $v_{n}$ wird jeweils mit der Wahrscheinlichkeit

$p={\frac {f(v_{n})}{k\cdot g(v_{n})}}$

akzeptiert (Acceptance), also dann, wenn erstmals $u_{n}<p$ ist. Die vorhergehenden Zufallszahlen werden dagegen verworfen (Rejection).

Einfaches Beispiel

Um eine Zufallszahl aus $\{1,2,3,4,5\}$ zu wählen, wobei jede Zahl mit der gleichen Wahrscheinlichkeit ${\tfrac 15}$ auftreten soll, kann man einen herkömmlichen Spielwürfel werfen. Erscheint eine 6, wirft man ein erneutes Mal. Meist wird aber bereits beim ersten Wurf eine Zahl zwischen 1 und 5 (einschließlich) erscheinen.

Implementierung

Programmiertechnisch wird die Verwerfungsmethode allgemein wie folgender Pseudocode realisiert:

   function F_verteilte_Zufallszahl()
     var x, u
     repeat
       x := G_verteilte_Zufallszahl()
       u := gleichförmig_verteilte_Zufallszahl()
     until u * k * g(x) < f(x)
     return x
   end

Der Erwartungswert für die Anzahl der Schleifendurchläufe ist (siehe unten, Effizienz).

Grafische Veranschaulichung

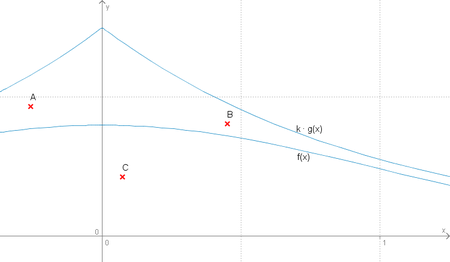
Beispiel: Der erste Treffer ist hier durch C angedeutet

Man kann sich die Methode so vorstellen, dass in der xy-Ebene zwischen der x-Achse und dem Graph von $k\cdot g(x)$ gleichmäßig auf der Fläche verteilte Zufallspunkte verstreut werden. Als x-Koordinate des Punkts nimmt man die G-verteilte Zufallszahl $v_{i}$ , und die y-Koordinate erhält man aus der standardverteilten Zahl $u_{i}$ : $y_{i}=u_{i}\cdot k\cdot g(v_{i})$ .

Von diesen Zufallspunkten werden diejenigen verworfen, die oberhalb des Graphs von f(x) liegen ( $y_{i}>f(v_{i})$ ). Die x-Koordinaten der übrigen Punkte sind dann nach der Dichtefunktion f(x) verteilt.

Um eine Zufallszahl nach dieser Verteilung zu erzeugen, werden also solange neue Zufallspunkte erzeugt, bis einer unterhalb von f(x) liegt (im Bild der Punkt C). Dessen x-Koordinate ist die gesuchte Zufallszahl.

Effizienz

Die Fläche unter der Dichtefunktion f(x) ist 1, und unter $k\cdot g(x)$ ist die Fläche entsprechend . Deshalb müssen im Mittel Standardzufallszahlen und Zufallszahlen, die genügen, verbraucht werden, bis der erste Treffer erzielt wird. Daher ist es von Vorteil, wenn die Hilfsdichte die Dichte möglichst gut approximiert, damit man klein wählen kann.

Basierend auf einem Artikel in:

Wikipedia.de