Poisson-Approximation

Vergleich der Poisson-Verteilung (schwarze Linien) und der Binomialverteilung mit

(rote Kreise),

(blaue Kreise),

(grüne Kreise). Alle Verteilungen haben einen Erwartungswert von 5. Die horizontale Achse zeigt die Anzahl der eingetretenen Ereignisse . Je größer wird, umso besser ist die Approximation der Binomialverteilung durch die Poisson-Verteilung.

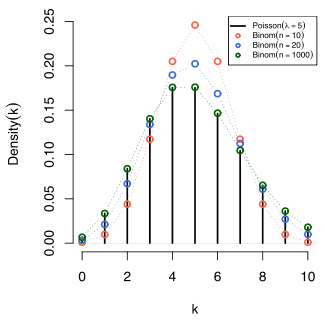
Die Poisson-Approximation ist in der Wahrscheinlichkeitsrechnung eine Möglichkeit, die Binomialverteilung und die verallgemeinerte Binomialverteilung für große Stichproben und kleine Wahrscheinlichkeiten durch die Poisson-Verteilung anzunähern. Durch den Grenzübergang nach unendlich erhält man dann die Konvergenz in Verteilung der beiden Binomialverteilungen gegen die Poisson-Verteilung.

Formulierung

Ist $(S_{n})$ eine Folge binomialverteilter Zufallsvariablen mit Parametern $n\in \mathbb {N}$ und $p_{n}$ , sodass für die Erwartungswerte $E(S_{n})=n\cdot p_{n}\to \lambda >0$ für $n\to \infty$ gilt, dann folgt

$P(S_{n}=k)=B_{{n,p_{n}}}(\{k\})\to \,{\frac {\lambda ^{k}}{k!}}{\mathrm {e}}^{{-\lambda }}=P_{\lambda }(\{k\})\quad$

${\text{für}}\quad n\to \infty$ .

Beweis-Skizze

Der Wert einer Poisson-verteilten Zufallsvariable an der Stelle ist der Grenzwert $n\to \infty$ einer Binomialverteilung mit $p=\tfrac{\lambda}{n}$ an der Stelle :

${\begin{aligned}\lim _{{n\to \infty }}P(S_{n}=k)&=\lim _{{n\to \infty }}{\frac {n!}{k!\,(n-k)!}}\left({\frac {\lambda }{n}}\right)^{{k}}\left(1-{\frac {\lambda }{n}}\right)^{{n-k}}\\&=\lim _{{n\to \infty }}\left({\frac {\lambda ^{{k}}}{k!}}\right)\left({\frac {n(n-1)(n-2)\cdots (n-k+1)}{n^{{k}}}}\right)\left(1-{\frac {\lambda }{n}}\right)^{{n}}\left(1-{\frac {\lambda }{n}}\right)^{{-k}}\\&={\frac {\lambda ^{{k}}}{k!}}\cdot \lim _{{n\to \infty }}\underbrace {\left({\frac {n}{n}}\cdot {\frac {n-1}{n}}\cdot {\frac {n-2}{n}}\cdots {\frac {n-k+1}{n}}\right)}_{{\to 1}}\underbrace {\left(1-{\frac {\lambda }{n}}\right)^{{n}}}_{{\to e^{{-\lambda }}}}\underbrace {\left(1-{\frac {\lambda }{n}}\right)^{{-k}}}_{{\to 1}}\\&={\frac {\lambda ^{{k}}{\mathrm {e}}^{{-\lambda }}}{k!}}.\end{aligned}}$

Bei großen Stichproben und kleinem lässt sich folglich die Binomialverteilung gut durch die Poisson-Verteilung approximieren.

Die Darstellung als Grenzwert der Binomialverteilung erlaubt eine alternative Berechnung von Erwartungswert und Varianz der Poisson-Verteilung. Seien $X_1,\dotsc,X_n \,n$ unabhängige bernoulliverteilte Zufallsvariablen mit $\,p=\lambda/n$ und sei $S_{n}:=X_{1}+\dotsb +X_{n}$ . Für $n\to \infty$ gilt $S_{n}\sim P_{{\lambda }}$ und

${\begin{aligned}\operatorname {E}(S_{n})&=\operatorname {E}(X_{1})+\dotsb +\operatorname {E}(X_{n})=\underbrace {{\frac {\lambda }{n}}+\dotsb +{\frac {\lambda }{n}}}_{{n\,{\mathrm {mal}}}}=\lambda \to \lambda \\\operatorname {Var}(S_{n})&=\operatorname {Var}(X_{1})+\dotsb +\operatorname {Var}(X_{n})\\&=\underbrace {{\frac {\lambda }{n}}\left(1-{\frac {\lambda }{n}}\right)+\dotsb +{\frac {\lambda }{n}}\left(1-{\frac {\lambda }{n}}\right)}_{{n\,{\mathrm {mal}}}}=\lambda \left(1-{\frac {\lambda }{n}}\right)\to \lambda .\end{aligned}}$

Güte der Approximation

Für die Fehlerabschätzung gilt

$\sum _{{k\geq 0}}\left|B_{{n,p}}(\{k\})-P_{{n\cdot p}}(\{k\})\right|\leq 2np^{2}$ .

Die Approximation einer Summe von Bernoulli-verteilten Zufallsvariablen (bzw. einer binomialverteilten Zufallsvariable) ist also insbesondere für kleine gut. Als Faustregel gilt, dass die Approximation gut ist, wenn $n\geq 50$ und $p\leq 0{,}05$ gilt. Ist $p\approx 0{,}5$ , so ist die Normal-Approximation besser geeignet.

Verallgemeinerung

Allgemeiner lässt sich Folgendes zeigen: Sind $X_{1},\dotsc ,X_{n}$ stochastisch unabhängige Zufallsvariablen mit $P(X_{i}=1)=p_{i}=1-P(X_{i}=0)$ (Jede Zufallsvariable ist also Bernoulli-verteilt). Dann ist

$S:=\sum _{{i=1}}^{n}X_{i}$

verallgemeinert binomialverteilt und es ist

$\lambda =\sum _{{i=1}}^{n}p_{i}$ .

Dann gilt

$\sum _{{k=0}}^{\infty }\left|P(S=k)-\exp(-\lambda ){\frac {\lambda ^{k}}{k!}}\right|\leq 2\sum _{{i=1}}^{n}p_{i}^{2}$ .

Gilt $p_{i}=p_{j}$ für alle $1\leq i,j\leq n$ , so ist binomialverteilt und das obige Ergebnis folgt sofort.

Beispiel

Ein Individuum einer Spezies zeugt n=1000 Nachkommen, die alle stochastisch unabhängig voneinander mit einer Wahrscheinlichkeit von $p_{i}=0{,}001$ das geschlechtsreife Alter erreichen. Interessiert ist man nun an der Wahrscheinlichkeit, dass zwei oder mehr Nachkommen das geschlechtsreife Alter erreichen.

Exakte Lösung

Sei $X_{i}=1$ die Zufallsvariable „Der -te Nachkomme erreicht das geschlechtsreife Alter“. Es gilt $P(X_{i}=1)=p_{i}$ > und $P(X_{i}=0)=1-p_{i}$ für alle . Dann ist die Anzahl der überlebenden Nachkommen $S:=\sum _{{i=1}}^{n}X_{i}$ aufgrund der stochastischen Unabhängigkeit $B_{{n,p}}$ -verteilt. Zur Modellierung definiert man den Wahrscheinlichkeitsraum $(\Omega ,\Sigma ,P)$ mit der Ergebnismenge $\Omega :=\{0,\dotsc ,n\}$ , der Anzahl der überlebenden geschlechtsreifen Nachkommen. Die σ-Algebra ist dann kanonisch die Potenzmenge der Ergebnismenge: $\Sigma :={\mathcal P}(\Omega )$ und als Wahrscheinlichkeitsverteilung die Binomialverteilung: $P(\{k\}):=B_{{n,p}}(\{k\})$ . Gesucht ist $P(S\geq 2)=1-P(S=1)-P(S=0)=1-B_{{1000;\,0{,}001}}(\{0\})-B_{{1000;\,0{,}001}}(\{1\})\approx 0{,}2642$ . Es erreichen also mit einer Wahrscheinlichkeit von ca. 26 % mindestens zwei Individuen das geschlechtsreife Alter.

Approximierte Lösung

Da ausreichend groß und ausreichend klein ist, lässt sich die Binomialverteilung genügend genau mittels der Poisson-Verteilung annähern. Diesmal ist der Wahrscheinlichkeitsraum $(\Omega ,\Sigma ,P)$ definiert mittels des Ergebnisraums $\Omega :={\mathbb {N}}$ , der $\sigma$ -Algebra $\Sigma :={\mathcal P}({\mathbb N})$ und der Poisson-Verteilung als Wahrscheinlichkeitsverteilung $P(\{k\}):=P_{\lambda }(\{k\})={\frac {\lambda ^{k}}{k!}}\,{\mathrm {e}}^{{-\lambda }}$ mit dem Parameter $\lambda =n\cdot p=1$ . Man beachte hier, dass die beiden modellierten Wahrscheinlichkeitsräume unterschiedlich sind, da die Poisson-Verteilung auf einem endlichen Ergebnisraum keine Wahrscheinlichkeitsverteilung definiert. Die Wahrscheinlichkeit, dass mindestens zwei Individuen das geschlechtsreife Alter erreichen, ist also $P(S\geq 2)\approx 1-P_{\lambda }(\{1\})-P_{\lambda }(\{0\})=1-{\frac {\lambda ^{1}}{1!}}e^{-1}-{\frac {\lambda ^{0}}{0!}}e^{-1}\approx 0{,}2642$ .

Bis auf vier Nachkommastellen stimmt also die exakte Lösung mit der Poisson-Approximation überein.

Basierend auf einem Artikel in Wikipedia.de