Geometrische Verteilung

Geometrische Verteilung
Wahrscheinlichkeitsverteilung 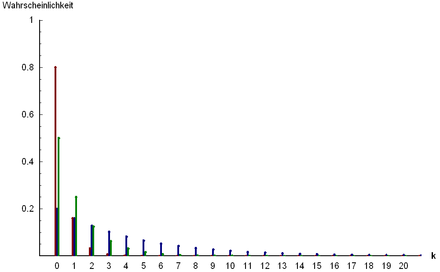Wahrscheinlichkeitsfunktion der geometrischen Verteilung (Variante B) für (blau), (grün) und (rot)
Verteilungsfunktion
Parameter	p ∈ (0,1) — Einzel-Erfolgs-Wahrscheinlichkeit
Erwartungswert	${\frac {1}{p}}$ (A) bzw. ${\frac {1-p}{p}}$ (B)
Varianz	$\frac{1-p}{p^2}$
Schiefe	$\frac{2-p}{\sqrt{1-p}}$
Wölbung	$9+\frac{p^2}{1-p}$

Die geometrische Verteilung ist eine Wahrscheinlichkeitsverteilung in der Stochastik, die univariat ist und zu den diskreten Wahrscheinlichkeitsverteilungen zählt. Sie wird aus unabhängigen Bernoulli-Experimenten abgeleitet und in zwei Varianten definiert:

Variante A: die Wahrscheinlichkeitsverteilung der Anzahl der Bernoulli-Versuche, die notwendig sind, um einen Erfolg zu haben. Diese Verteilung ist auf der Menge $\mathbb {N}$ definiert.
Variante B: die Wahrscheinlichkeitsverteilung der Anzahl der Fehlversuche vor dem ersten Erfolg. Diese Verteilung ist auf der Menge $\mathbb {N} _{0}$ definiert.

Die beiden Varianten stehen in der Beziehung X=Y+1 . Welche davon man „geometrische Verteilung“ nennt, wird entweder vorher festgelegt oder man wählt diejenige, die gerade zweckmäßiger ist.

Die geometrische Verteilung wird verwendet:

bei der Analyse der Wartezeiten bis zum Eintreffen eines bestimmten Ereignisses.
- bei der Lebensdauerbestimmung von Geräten und Bauteilen, d.h. dem Warten bis zum ersten Ausfall
bei der Bestimmung der Anzahl häufiger Ereignisse zwischen unmittelbar aufeinanderfolgenden seltenen Ereignissen wie zum Beispiel Fehlern:
- Bestimmung der Zuverlässigkeit von Geräten (MTBF)
- Bestimmung des Risikos in der Versicherungsmathematik
- Bestimmung der Fehlerrate in der Datenübertragung, zum Beispiel Anzahl der erfolgreich übertragenen TCP-Pakete zwischen zwei Paketen mit Retransmission

Definition der geometrischen Verteilung

Eine diskrete Zufallsgröße oder mit dem Parameter (Wahrscheinlichkeit für einen Erfolg), q=1-p (Wahrscheinlichkeit für einen Misserfolg) genügt der geometrischen Verteilung G(p) , wenn:

Variante A: Für die Wahrscheinlichkeit, dass man genau Versuche benötigt, um zum ersten Erfolg zu kommen, gilt; $\operatorname {P}(X=n)=p(1-p)^{{n-1}}=pq^{{n-1}}\quad (n=1,2,\dotsc )$
Variante B: Für die Wahrscheinlichkeit, Fehlversuche vor dem ersten Erfolg zu haben, gilt; $\operatorname {P}(Y=n)=p(1-p)^{{n}}=pq^{{n}}\quad (n=0,1,2,\dotsc )$

In beiden Fällen bilden die Werte für die Wahrscheinlichkeiten eine geometrische Folge.

Damit besitzt die geometrische Verteilung die folgenden Verteilungsfunktionen

Variante A: $F(n)=\operatorname {P} (X\leq n)=p\sum _{i=1}^{n}q^{i-1}=p\sum _{i=0}^{n-1}q^{i}=p{\frac {1-q^{n}}{1-q}}=1-q^{n}=1-(1-p)^{n}$
Variante B: $F(n)=\operatorname {P} (Y\leq n)=p\sum _{i=0}^{n}q^{i}=p{\frac {1-q^{n+1}}{1-q}}=1-q^{n+1}=1-(1-p)^{n+1}$

Eigenschaften

Erwartungswert

Die Erwartungswerte der beiden geometrischen Verteilungen sind

Variante A: $\operatorname {E}(X)={\frac {1}{p}}$
Variante B: $\operatorname {E}(Y)=\operatorname {E}(X)-1={\frac {1-p}{p}}$ .

Der Erwartungswert kann auf verschiedene Weisen hergeleitet werden:

$\operatorname {E} (X)=p\sum _{k=1}^{\infty }k\,(1-p)^{k-1}=p\sum _{k=0}^{\infty }\,{\frac {\mathrm {d} }{\mathrm {d} p}}\left(-(1-p)^{k}\right)=-p{\frac {\mathrm {d} }{\mathrm {d} p}}\left(\sum _{k=0}^{\infty }\,(1-p)^{k}\right)=-p{\frac {\mathrm {d} }{\mathrm {d} p}}\left({\frac {1}{p}}\right)={\frac {1}{p}}$ .

$\operatorname {E} (X)=\sum _{k=1}^{\infty }kp(1-p)^{k-1}=\sum _{k=0}^{\infty }(k+1)p(1-p)^{k}=\sum _{k=0}^{\infty }kp(1-p)^{k}+\sum _{k=1}^{\infty }p(1-p)^{k-1}=(1-p)\operatorname {E} (X)+1$

$\Rightarrow \operatorname {E} (X)={\frac {1}{p}}$ .

Dabei ist $\sum _{{k=1}}^{{\infty }}p(1-p)^{{k-1}}=1$ , da $p(1-p)^{{k-1}}$ die Wahrscheinlichkeitsfunktion ist.

Der Erwartungswert $\operatorname {E} (X)$ lässt sich per Fallunterscheidung zerlegen. Mit Wahrscheinlichkeit geht das erste Experiment erfolgreich aus, das heißt, wird mit 1 realisiert. Mit Wahrscheinlichkeit ist das erste Experiment erfolglos, aber der Erwartungswert für die Anzahl der dann noch folgenden Experimente ist wegen der Gedächtnislosigkeit wiederum $\operatorname {E} (X)$ . Also gilt

$\operatorname {E}(X)=p\cdot 1+(1-p)\cdot (1+\operatorname {E}(X))=1+(1-p)\cdot \operatorname {E}(X)$ , also $\operatorname {E}(X)={\frac {1}{p}}$ .

Führt man Experimente durch, so ist der Erwartungswert für die Anzahl der erfolgreichen Experimente $n\cdot p$ . Daher ist der zu erwartende Abstand zwischen zwei erfolgreichen Experimenten (einschließlich eines erfolgreichen Experimentes) ${\tfrac {n}{n\cdot p}}$ , also $\operatorname {E}(X)={\tfrac {1}{p}}$ .

Varianz

Die Varianzen der beiden geometrischen Verteilungen sind

$\operatorname {Var}(X)=\operatorname {Var}(Y)={\frac {1-p}{p^{2}}}={\frac {1}{p^{{2}}}}-{\frac {1}{p}}$ .

Die Herleitung kann erfolgen über

$\operatorname{Var}(X)$	$=\operatorname {E}(X^{2})-\operatorname {E}(X)^{2}=p\sum _{{k=1}}^{{\infty }}k^{{2}}(1-p)^{{k-1}}-{\frac {1}{p^{2}}}$
	$=p\sum _{{k=1}}^{{\infty }}k(k+1)(1-p)^{{k-1}}-p\sum _{{k=1}}^{{\infty }}k(1-p)^{{k-1}}-{\frac {1}{p^{2}}}$
	$=p{\frac {\mathrm {d} ^{2}}{\mathrm {d} p^{2}}}\sum _{k=1}^{\infty }(1-p)^{k+1}+p{\frac {\mathrm {d} }{\mathrm {d} p}}\sum _{k=1}^{\infty }(1-p)^{k}-{\frac {1}{p^{2}}}$
	$=p{\frac {\mathrm {d} ^{2}}{\mathrm {d} p^{2}}}\left(\sum _{k=0}^{\infty }(1-p)^{k}\cdot (1-p)^{2}\right)+p{\frac {\mathrm {d} }{\mathrm {d} p}}\left(\sum _{k=0}^{\infty }(1-p)^{k}\cdot (1-p)\right)-{\frac {1}{p^{2}}}$
	$=p{\frac {\mathrm {d} ^{2}}{\mathrm {d} p^{2}}}\left({\frac {1}{1-(1-p)}}\cdot (1-p)^{2}\right)+p{\frac {\mathrm {d} }{\mathrm {d} p}}\left({\frac {1}{1-(1-p)}}\cdot (1-p)\right)-{\frac {1}{p^{2}}}$
	$=p{\frac {\mathrm {d} ^{2}}{\mathrm {d} p^{2}}}\left({\frac {(1-p)^{2}}{p}}\right)+p{\frac {\mathrm {d} }{\mathrm {d} p}}\left({\frac {1-p}{p}}\right)-{\frac {1}{p^{2}}}$
	$=p\cdot {\frac {2}{p^{3}}}-p\cdot {\frac {1}{p^{2}}}-{\frac {1}{p^{2}}}={\frac {2}{p^{{2}}}}-{\frac {1}{p}}-{\frac {1}{p^{2}}}={\frac {1}{p^{{2}}}}-{\frac {1}{p}}$ .

Gedächtnislosigkeit

Die geometrische Verteilung ist eine gedächtnislose Verteilung, d.h., es gilt für

Variante A

$\operatorname {P}(X=n+k\,|\,X>n)=\operatorname {P}(X=k)\quad n,k=1,2,\dotsc$

Variante B

$\operatorname {P}(Y=n+k\,|\,Y\geq n)=\operatorname {P}(Y=k)\quad n,k=0,1,2,\dotsc$

Ist also von einer geometrisch verteilten Zufallsvariablen bekannt, dass sie größer als der Wert ist (Variante A) bzw. mindestens den Wert hat (Variante B), so ist die Wahrscheinlichkeit, dass sie diesen Wert um übertrifft, genau so groß wie die, dass eine identische Zufallsvariable überhaupt den Wert annimmt.

Die Gedächtnislosigkeit ist eine definierende Eigenschaft; die geometrische Verteilung ist also die einzig mögliche gedächtnislose diskrete Verteilung. Ihr stetiges Pendant hierbei ist die Exponentialverteilung.

Bezug zur Reproduktivität

Die Summe $\textstyle X=\sum _{{i=1}}^{{k}}X_{{i}}$ unabhängiger geometrisch verteilter Zufallsgrößen $X_{1},\dotsc ,X_{k}$ mit demselben Parameter ist nicht geometrisch verteilt, sondern negativ binomialverteilt. Somit ist die Familie der geometrischen Wahrscheinlichkeitsverteilungen nicht reproduktiv.

Schiefe

Die Schiefe ergibt sich für beide Varianten zu:

$\operatorname {v}(X)=\operatorname {v}(Y)={\frac {2-p}{{\sqrt {1-p}}}}$ .

Wölbung

Die Wölbung lässt sich für beide Varianten ebenfalls geschlossen darstellen als

$\beta _{2}=9+{\frac {p^{2}}{1-p}}$ .

Damit ist der Exzess

$\gamma =6+{\frac {p^{2}}{1-p}}$ .

Modus

Variante A

Bei Variante A ist der Modus 1.

Variante B

Bei Variante B ist der Modus 0.

Median

Variante A

Bei Variante A ist der Median

${\tilde m}=\left\lceil {\frac {-1}{\log _{2}(1-p)}}\right\rceil \!$ .

Hierbei ist $\lceil \cdot \rceil$ die Gaussklammer. Der Median ist nicht notwendigerweise eindeutig.

Variante B

Hier ist der Median

${\tilde m}=\left\lceil {\frac {-1}{\log _{2}(1-p)}}\right\rceil -1\!$ .

Auch er muss nicht eindeutig sein.

Entropie

Die Entropie beider Varianten ist

$\mathrm{H} ={\tfrac {-(1-p)\log _{2}(1-p)-p\log _{2}p}{p}}$ .

Charakteristische Funktion

Die charakteristische Funktion hat die Form

Variante A: $\varphi _{X}(s)={\frac {pe^{is}}{1-(1-p)e^{is}}}$ .
Variante B: $\varphi _{Y}(s)={\frac {p}{1-(1-p)e^{is}}}$ .

Momenterzeugende Funktion

Die momenterzeugende Funktion der geometrischen Verteilung ist

Variante A: $M_{{X}}(s)={\frac {pe^{s}}{1-(1-p)e^{{s}}}}$
Variante B: > $M_{{Y}}(s)={\frac {p}{1-(1-p)e^{{s}}}}$ .

Wahrscheinlichkeitserzeugende Funktion

Die wahrscheinlichkeitserzeugende Funktion der geometrischen Verteilung ist

Variante A: $m_{{X}}(t)={\frac {pt}{1-(1-p)t}}$
Variante B: $m_{{Y}}(t)={\frac {p}{1-(1-p)t}}$ .

Beziehungen zu anderen Verteilungen

Beziehung zur negativen Binomialverteilung

Verallgemeinerung auf mehrere Erfolge
Eine Verallgemeinerung der geometrischen Verteilung stellt die negative Binomialverteilung dar, die die Wahrscheinlichkeit angibt, dass für Erfolge Versuche notwendig sind bzw. (in einer alternativen Darstellung) dass der -te Erfolg eintritt, nachdem bereits k=n-r Misserfolge eingetreten sind.

Umgekehrt ist die geometrische Verteilung eine negative Binomialverteilung mit r=1 . Somit gilt für die Faltung der geometrische Verteilung $\operatorname {Geom} (p)*\operatorname {Geom} (p)=\operatorname {NegBin} (2,p)$ .

Beziehung zur Exponentialverteilung

Konvergenz der geometrischen Verteilung
Für eine Folge $X_{1},X_{2},X_{3},\dotsc$ geometrisch verteilter Zufallsvariablen mit Parametern $p_{1},p_{2},p_{3},\dotsc$ gelte $\lim _{{n\to \infty }}np_{n}=\lambda$ mit einer positiven Konstante $\lambda$ . Dann konvergiert die Folge ${\tfrac {X_{n}}{n}}$ für große gegen eine exponentialverteilte Zufallsvariable mit Parameter $\lambda$ .

In Analogie zur diskreten geometrischen Verteilung bestimmt die stetige Exponentialverteilung die Wartezeit bis zum ersten Eintreffen eines seltenen Poisson-verteilten Ereignisses. Die Exponentialverteilung ist also das kontinuierliche Analogon zur diskreten geometrischen Verteilung.

Beziehung zur zusammengesetzten Poisson-Verteilung

Die geometrische Verteilung in der Variante B entsteht als Spezialfall der zusammengesetzten Poisson-Verteilung in Kombination mit der logarithmischen Verteilung. Als Parameter wählt man $p_{{\text{log}}}=1-p_{{\text{geom}}}$ und $-\lambda =\ln(1-p_{{\text{log}}})$ . Damit ist die geometrische Verteilung auch unendlich teilbar.

Beziehung zum Urnenmodell

Die geometrische Verteilung lässt sich aus dem Urnenmodell herleiten, wenn $p={\frac {p_{1}}{p_{2}}}\in {\mathbb {Q}}$ ist. Dann entsteht die geometrische Verteilung beim Ziehen mit Zurücklegen aus einer Urne mit $p_{2}$ Kugeln, von denen $p_{1}$ markiert sind. Sie ist dann die Wartezeit auf den ersten Erfolg.

Zufallszahlen

Zufallszahlen zur geometrischen Verteilung werden üblicherweise mit Hilfe der Inversionsmethode erzeugt. Diese Methode bietet sich bei der geometrischen Verteilung besonders an, da die Einzelwahrscheinlichkeiten der einfachen Rekursion $\operatorname {P}(X=k+1)=(1-p)\operatorname {P}(X=k)$ genügen. Die Inversionsmethode ist hier also nur mit rationalen Operationen (Addition, Multiplikation) und ohne die Verteilungsfunktion vorher zu berechnen und abzuspeichern durchführbar, was einen schnellen Algorithmus zur Simulation garantiert.

Basierend auf einem Artikel in:

Wikipedia.de