Lambertsche W-Funktion

Der Graph von W(x) für W > −4 und x < 6. Der obere Zweig W ≥ −1 ist die Funktion W₀ (principal branch), der untere Zweig mit W ≤ −1 ist die Funktion W₋₁.

In der Mathematik ist die lambertsche W-Funktion (oder Lambert-W-Funktion), auch Omegafunktion oder Produktlogarithmus, benannt nach Johann Heinrich Lambert, die Umkehrfunktion von

$f\colon x\mapsto xe^{x},$

wobei $e^{x}$ die Exponentialfunktion ist. Die lambertsche W-Funktion wird meistens mit W(x) bezeichnet. Es gilt

$z=W(z)e^{{W(z)}},z\in {\mathbb C}.$

Eigenschaften

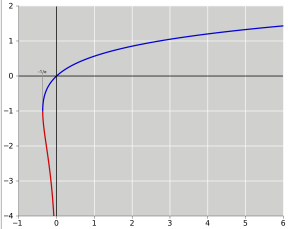
Im Reellen

Die zwei Funktionsäste $W_{0}$ und $W_{{-1}}$

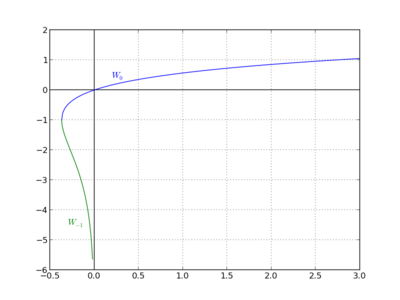
Da die Funktion auf dem Intervall $\left(-\infty ,0\right]$ nicht injektiv ist, besitzt die lambertsche W-Funktion auf dem Intervall $\left[-{\tfrac 1e},0\right)$ zwei Funktionsäste $W_{0}(x)$ und $W_{{-1}}(x)$ . Mit W(x) wird aber in der Regel der obere der Äste bezeichnet.

Die W-Funktion kann nicht als elementare Funktion ausgedrückt werden.

Zumeist wird sie in der Kombinatorik verwendet, beispielsweise zur Auswertung von Bäumen oder zur asymptotischen Bestimmung der Bell-Zahlen.

Die Ableitungsfunktion eines Astes der W-Funktion kann mit Hilfe der Umkehrregel der Differentialrechnung gefunden werden (an der Stelle -1/e existiert die Ableitung nicht, ihr Betrag wächst bei hinreichender Annäherung an diese Stelle in jedem Ast über alle Schranken):

$W'(x)={\frac {W(x)}{x(1+W(x))}}{\text{ für }}x>-{\frac {1}{e}},x\neq 0$

sowie $W'_{0}(0)=1$ für den oberen Ast (der untere Ast ist für $x\geq 0$ gar nicht definiert).

Die Ableitungen höherer Ordnung haben die Form

${\frac {\mathrm {d} ^{n}W(x)}{\mathrm {d} x^{n}}}={\frac {(-1)^{n+1}W^{n}(x)}{x^{n}(1+W(x))^{2n-1}}}\cdot P_{n}(W(x)),$

wobei die $P_{n}$ Polynome sind, die sich aus folgender Rekursionsformel berechnen lassen:

$P_{n+1}(t)=(nt+3n-1)\cdot P_{n}(t)-(t+1)\cdot P_{n}'(t),\quad n\geq 1$

Ausgehend von $P_{1}(t)=1$ ergeben sich damit die nächsten drei Ableitungen zu:

${\begin{aligned}W''(x)&=-{\frac {W^{2}(x)}{x^{2}(1+W(x))^{3}}}\cdot (W(x)+2)\\W^{(3)}(x)&=+{\frac {W^{3}(x)}{x^{3}(1+W(x))^{5}}}\cdot (2W^{2}(x)+8W(x)+9)\\W^{(4)}(x)&=-{\frac {W^{4}(x)}{x^{4}(1+W(x))^{7}}}\cdot (6W^{3}(x)+36W^{2}(x)+79W(x)+64)\end{aligned}}$

Eine Stammfunktion ergibt sich durch Substitution des ganzen Integranden:

$\int W(x)\,{\mathrm d}x=x\left(W(x)-1+{\frac 1{W(x)}}\right)+C$

Durch implizites Differenzieren kann man zeigen, dass folgender Differentialgleichung genügt:

$z(1+W){\frac {\mathrm {d} W}{\mathrm {d} z}}=W\quad {\text{mit }}z\neq -{\frac {1}{e}}$

Die Taylor-Reihe von um $x_{0}=0$ ist gegeben durch

$W(x)=\sum _{{n=1}}^{\infty }{\frac {(-n)^{{n-1}}}{n!}}\ x^{n}=x-x^{2}+{\frac 32}x^{3}-{\frac 83}x^{4}+{\frac {125}{24}}x^{5}-\dotsb .$

Der Konvergenzradius beträgt ${\tfrac 1e}$ .

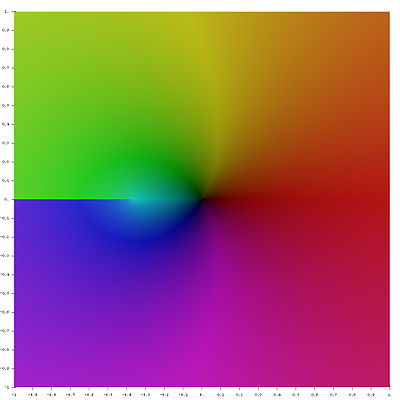
Im Komplexen

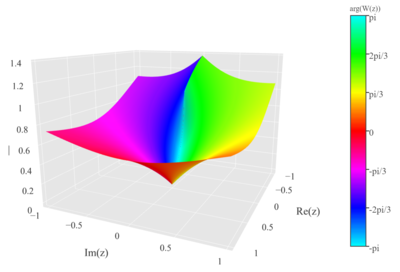
Der Hauptzweig der W-Funktion auf der komplexen Zahlenebene. Man beachte den Bruch entlang der negativen reellen Halbachse ab $-e^{-1}$ . Die Koordinaten eines Punkts beschreiben Real- und Imaginärteil des Arguments, die Helligkeit beschreibt den Betrag und der Farbton die Phase des Ergebnisses.

Radius des Hauptzweigs der W-Funktion als Höhe, Farbton die Phase

Für jedes $k\in \mathbb {Z}$ gibt es einen Zweig der W-Funktion, wobei k=0 und k=-1 die oben genannten reellen Zweige darstellen. Der Hauptzweig $W_{0}$ ist insofern besonders, als er auf der gesamten komplexen Zahlenebene definiert ist; alle anderen Zweige (Nebenzweige) haben eine Definitionslücke bei z=0 . Konkret gilt

$W_{0}(0)=0$ und

$\lim _{z\to 0}W_{k}(z)=-\infty$ für alle $k\neq 0$ .

Dieses Verhalten ist im Diagramm oben für die reellen Fälle exemplarisch ersichtlich.

Die Verzweigungsstelle für den Hauptzweig ist bei $z=-{\tfrac {1}{e}}$ , die sich über den Rest der negativen Halbachse in Richtung $-\infty$ erstreckt. Diese Verzweigung trennt den Hauptzweig von den Nebenzweigen $W_{{-1}}$ und $W_{+1}$ . Auf den Nebenzweigen beginnt die Verzweigung bereits bei z=0 und setzt sich wie beim Hauptzweig in Richtung $-\infty$ fort.

Alle Zweige sind injektiv und ihre Wertebereiche sind disjunkt. Aufgefasst als Funktion mit zwei Parametern aus $\mathbb {Z}$ und $\mathbb {C}$ hat die W-Funktion die gesamte komplexe Zahlenebene als Wertebereich. Das Bild der reellen Achse ist die Vereinigung der reellen Achse mit der Quadratrix des Hippias, der für $t\in \mathbb {R} \setminus \{k\pi \mid k\in \mathbb {Z} \setminus \{0\}\}$ definierten parametrischen Kurve $w(t)=-t\cot t+it$ , wobei man unter $w(0)$ den Grenzwert $\lim _{t\to 0}w(t)=-1$ versteht, wodurch an der Stelle t=0 stetig fortgesetzt wird.

Spezielle Werte

$W\left(-{\frac {\pi }{2}}\right)={\frac {{\mathrm i}\pi }2}$

$W\left(-{\frac 1e}\right)=-1$

$W\left(-{\frac {\ln 2}{2}}\right)=-\ln 2$

$W\left(0\right)=0$

$W\left(1\right)=0{,}5671432904\dots =:\Omega$ (die Omega-Konstante)

$W\left(e\right)=1$

Eigenschaften

$\int _{{0}}^{{+\infty }}W\left({\frac {1}{x^{2}}}\right)\,{\mathrm d}x={\sqrt {2\pi }}$
$\int _{0}^{+\infty }{\frac {W(x)}{x{\sqrt {x}}}}\,\mathrm {d} x={\sqrt {8\pi }}$
$\int _{0}^{\pi }W\left(2\cot ^{2}(x)\right)\sec ^{2}(x)\,\mathrm {d} x={\sqrt {16\pi }}$

Verwendung außerhalb der Kombinatorik

Die lambertsche W-Funktion kann gebraucht werden, um Gleichungen vom Typus

$a(x)e^{a(x)}=y$

zu lösen ( a(x) ist ein beliebiger, von abhängiger Ausdruck).

Auch die Gleichung

$x^{x}=z$

kann mit Hilfe der lambertschen W-Funktion gelöst werden. Die Lösung lautet

$x={\frac {\ln z}{W(\ln z)}}=\exp \left(W(\ln z)\right).$

Der unendliche Potenzturm

$x\uparrow \uparrow \infty :=x^{x^{x^{\cdot ^{\cdot ^{\cdot }}}}}$

kann an den konvergenten Stellen mit der W-Funktion in geschlossene Form gebracht werden:

$x\uparrow \uparrow \infty ={\frac {W(\ln {\frac {1}{x}})}{\ln {\frac {1}{x}}}}.$

Verallgemeinerungen

Mit Hilfe der normalen lambertschen W-Funktion lassen sich die exakten Lösungen „transzendenter algebraischer“ Gleichungen (in x) folgender Form ausdrücken:

$e^{-cx}=a_{0}(x-r)~~\quad \qquad \qquad \qquad \quad (1)$

mit reellen Konstanten $a_{0},c$ und . Die Lösung ist $x=r+{\frac {1}{c}}W\left({\frac {ce^{-cr}}{a_{0}}}\right)$ . Verallgemeinerungen der lambertschen W-Funktion umfassen:

Eine Anwendung auf dem Gebiet der allgemeinen Relativitätstheorie und der Quantenmechanik (Quantengravitation) in niedrigeren Dimensionen, die eine zuvor unbekannte Verknüpfung zwischen beiden Gebieten aufzeigte, siehe Journal of Classical and Quantum Gravity, 24, 2007, S. 4647–4659 wobei die rechte Seite von Gleichung (1) nun ein quadratisches Polynom in ist:

$e^{-cx}=a_{0}(x-r_{1})(x-r_{2})~~\qquad \qquad (2)$

Hierbei sind $r_{1}$ und $r_{2}$ voneinander verschiedene reelle Konstanten, die Wurzeln des quadratischen Polynoms. Die Lösung ist eine Funktion allein des Arguments , aber $r_{i}$ und $a_{0}$ sind Parameter dieser Funktion. Insofern ähnelt diese Verallgemeinerung der hypergeometrischen Funktion und der Meijerschen G-Funktion, aber sie gehört zu einer anderen „Klasse“ von Funktionen. Wenn $r_{1}=r_{2}$ , so können beide Seiten von (2) faktorisiert und auf (1) reduziert werden, sodass sich die Lösung auf die normale lambertsche W-Funktion reduziert. Gleichung (2) entspricht der Gleichung für das „Dilaton“-Feld, von dem die Metrik des „linealen“ Zwei-Körper-Gravitationsproblems in 1 + 1 Dimensionen (eine räumliche und eine zeitliche Dimension) für den Fall ungleicher (Ruhe-)Massen abgeleitet ist, sowie dem Problem der Eigenwertberechnung für das quantenmechanische Doppelminimum-Dirac-Deltafunktions-Modell in einer Dimension und mit „ungleichen“ Ladungen.

Analytische Lösungen der Energie-Eigenwerte für einen speziellen Fall des quantenmechanischen Analogons des Eulerschen Drei-Körper-Problems, nämlich des (drei-dimensionalen) Wasserstoffmolekül-Ions. Hier ist nun die rechte Seite von (1) (oder (2)) das Verhältnis von zwei Polynomen unendlicher Ordnung in :

$e^{-cx}=a_{0}{\frac {\prod _{i=1}^{\infty }(x-r_{i})}{\prod _{i=1}^{\infty }(x-s_{i})}}\qquad \qquad \qquad (3)$

mit paarweise verschiedenen reellen Konstanten $r_{i}$ und $s_{i}$ sowie als Funktion des Energie-Eigenwertes und des Kern-Kern-Abstands . Gleichung (3), mit den Spezialfällen (1) und (2), steht in Beziehung zu einer großen Klasse retardierter Differentialgleichungen. Mit Hilfe von Hardys Begriff der „falschen Ableitung“ wurden exakte mehrfache Wurzeln für spezielle Fälle von Gleichung (3) gefunden. Die Anwendungen der lambertschen W-Funktion auf grundlegende physikalische Probleme sind damit selbst für die normale lambertsche W-Funktion, siehe (1), keineswegs erschöpft. Dies zeigen jüngste Beispiele aus dem Gebiet der Atom-, Molekül- und optischen Physik.

Numerische Berechnung

Eine Folge von Näherungen an die W-Funktion kann rekursiv mithilfe der Beziehung

$w_{j+1}=w_{j}-{\frac {w_{j}e^{w_{j}}-z}{e^{w_{j}}(w_{j}+1)-{\frac {(w_{j}+2)(w_{j}e^{w_{j}}-z)}{2w_{j}+2}}}}$

berechnet werden. Alternativ kann auch das Newton-Verfahren zur Lösung der Gleichung $we^{w}-z=0$ verwendet werden:

$w_{j+1}=w_{j}-{\frac {w_{j}e^{w_{j}}-z}{e^{w_{j}}+e^{w_{j}}w_{j}}}$ .

Tabelle reeller Funktionswerte

$W_{0},$ oberer Zweig:

${\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c}x&-0{,}3679&-0{,}34&-0{,}2&0&0{,}3&0{,}7&1{,}2&2&3&4&6&10&20&40&+\infty \\\hline y&-1&-0{,}6537&-0{,}2592&0&0{,}2368&0{,}4475&0{,}6356&0{,}8526&1{,}0499&1{,}2022&1{,}4324&1{,}7455&2{,}205&2{,}6968&+\infty \\\end{array}}$

$W_{{-1}},$ unterer Zweig:

${\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c|c|c|c}x&-0{,}3679&-0{,}365&-0{,}355&-0{,}31&-0{,}25&-0{,}18&-0{,}1&-0{,}05&-0{,}025&-0{,}01&-0{,}005&-0{,}001&-0{,}0001&0\\\hline y&-1&-1{,}1307&-1{,}2912&-1{,}7044&-2{,}1533&-2{,}7128&-3{,}5772&-4{,}4998&-5{,}3696&-6{,}4728&-7{,}284&-9{,}118&-11{,}6671&-\infty \\\end{array}}$

Andere Werte lassen sich leicht über $x=y\,e^{y}$ berechnen.

Eine Näherung von $W_{0}(x)$ für große ist

$W_{0}(x)\approx \ln(x)-\ln(\ln(x))+\ln(\ln(x))/\ln(x).$

Basierend auf einem Artikel in:

Wikipedia.de