Umkehrregel

$\tan \alpha =\tan(90^{\circ }-\beta )={\frac {1}{\tan \beta }}$

${\color {Periwinkle}f'}(x)={\frac {1}{{\color {Salmon}(f^{{-1}})'}({\color {Blue}f}(x))}}$

${\color {Periwinkle}f'}(x_{0})={\frac {1}{4}}$
${\color {Salmon}(f^{{-1}})'}({\color {Blue}f}(x_{0}))=4~$

Die Umkehrregel (manchmal auch Inversenregel genannt) ist eine Regel der Differentialrechnung. Sie besagt, dass für eine umkehrbare (das heißt bijektive) reelle Funktion ,

die an der Stelle differenzierbar ist und
dort keine waagerechte Tangente besitzt, d.h. für die $f'(x)\neq 0$ gilt,

auch ihre Umkehrfunktion $f^{-1}$ an der Stelle y=f(x) differenzierbar ist mit Ableitung

$(f^{{-1}})'(y)={\frac {1}{f'(f^{{-1}}(y))}}={\frac {1}{f'(x)}}.$

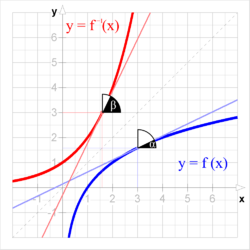
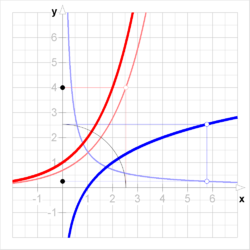
Die Gültigkeit dieser Gleichung kann man sich gut an einer Skizze verdeutlichen: Die Bildung der Umkehrfunktion entspricht einer Vertauschung der Koordinaten und . Die Graphen der Funktion und ihrer Umkehrfunktion $f^{-1}$ sind also zueinander symmetrisch bezüglich der Winkelhalbierenden des I. und III. Quadranten mit der Gleichung y=x . Die Ableitung einer Funktion an einer bestimmten Stelle entspricht der Steigung der zugehörigen Tangente, also gleich dem Tangens des Neigungswinkels gegenüber der Waagrechten. Damit erhält man:

$f'(x)=\tan \alpha =\tan(90^{\circ }-\beta )={\frac {1}{\tan \beta }}={\frac {1}{(f^{{-1}})'(f(x))}}.$

Beweisskizzen

Die Umkehrregel kann direkt gezeigt werden, indem man den Differenzenquotient

${\frac {f(x+h)-f(x)}{h}}$

dahingehend umformt, dass er zu

${\frac {1}{{\frac {f^{{-1}}(f(x+h))-f^{{-1}}(f(x))}{f(x+h)-f(x)}}}}$

wird, um anschließend mit t=f(x+h)-f(x) zu substituieren. Beim Grenzübergang für $h\to 0$ und damit auch $t\to 0$ (man beachte, dass differenzierbare Funktionen insbesondere stetig sind) folgt die Behauptung.

Alternativ ergibt unter Nutzung der Kettenregel die Eigenschaft

$f\left(f^{{-1}}(y)\right)=y$

der Umkehrfunktion bei Differenzieren nach auf beiden Seiten der Gleichung ebenfalls die Umkehrregel (mit $f^{{-1}}(y)=x$ ):

$f'\left(f^{{-1}}(y)\right)\cdot \left(f^{{-1}}\right)'(y)=1.$

Allerdings wird dabei die Differenzierbarkeit von $f^{-1}$ an der Stelle schon vorausgesetzt, während sie in der ersten Beweisskizze mitbewiesen wird.

Ganz ähnlich erhält man auch einen Ausdruck für die 2. Ableitung der Umkehrfunktion $\left(f^{{-1}}\right)''(y)$ , indem man die letzte Gleichung erneut nach differenziert unter Anwendung der Produktregel (wieder ist $f^{{-1}}(y)=x$ bzw. f(x)=y ):

$\left(f^{{-1}}\right)''(y)=-{\frac {f''(x)}{\left(f'(x)\right)^{3}}}.$

Beispiele

Die Umkehrfunktion der Exponentialfunktion $y=f(x)=e^{x}$ ist der natürliche Logarithmus

$f^{-1}(y)=\ln(y)\,.$

Wegen f'(x) = e^x gilt also

$\ln '(y)={\frac {1}{e^{\ln(y)}}}={\frac {1}{y}}\,.$

Eine weitere wichtige Anwendung der Umkehrregel sind die Ableitungen der Umkehrfunktionen der trigonometrischen Funktionen. So gilt z.B. für die Ableitung des Arkussinus für $-1<y<1$ wegen $\sin '=\cos$

$\arcsin '(y)={\frac {1}{\cos \left(\arcsin(y)\right)}}\,.$

Stellt man den trigonometrischen Pythagoras nach dem Kosinus um, erhält man

$\cos(y)={\sqrt {1-\sin ^{2}(y)}}$ .

Wegen $f(f^{-1}(y))=y$ folgt daraus:

$\arcsin '(y)={\frac {1}{\sqrt {1-\sin ^{2}\left(\arcsin(y)\right)}}}={\frac {1}{\sqrt {1-y^{2}}}}\,.$

Analoges gilt für die Ableitungen des Arkuskosinus und des Arkustangens.

Alternative Formulierungen und Verallgemeinerungen

Alternative Voraussetzungen

Fordert man die Stetigkeit der ersten Ableitung von , so genügt bereits die Voraussetzung $f'(x)\neq 0$ , da daraus direkt $f'\neq 0$ auf einem kleinen Bereich um und daraus wiederum die Existenz der Umkehrfunktion von auf diesem kleinen Bereich folgt (man betrachte dazu die Monotonie von !). Von dieser Grundidee geht man bei der mehrdimensionalen Verallgemeinerung der Umkehrregel, dem Satz von der inversen Abbildung, aus.

Abweichende Schreibweisen in der Physik und anderen Naturwissenschaften

In der Physik und anderen Naturwissenschaften wird manchmal die leibnizsche Schreibweise mit Differentialen benutzt. Die Umkehrregel nimmt dann die folgende Gestalt an:

${\frac {{\mathrm d}y}{{\mathrm d}x}}={\frac {1}{{\frac {{\mathrm d}x}{{\mathrm d}y}}}}.$

Verallgemeinerungen

Die Umkehrregel lässt sich auf die Ableitungen von Funktionen in mehreren Dimensionen verallgemeinern. Die mehrdimensionale Entsprechung der Umkehrregel ist der Satz von der Umkehrabbildung.

Literatur

Konrad Königsberger: Analysis 1. 6. durchgesehene Auflage. Springer, Berlin u. a. 2004, ISBN 3-540-40371-X, (Springer-Lehrbuch).

Basierend auf einem Artikel in:

Wikipedia.de