Trigonometrischer Pythagoras

Geometrische Veranschaulichung
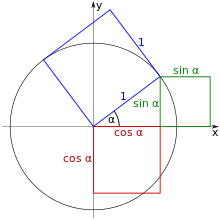
des „trigonometrischen Pythagoras“

Als „trigonometrischer Pythagoras“ wird die Identität

$\sin^2 \alpha+\cos^2 \alpha = 1$

bezeichnet. Hierbei steht $\sin^2 \alpha$ für $(\sin \alpha)^2$ und $\cos^2 \alpha$ für $(\cos \alpha)^2$ . Die Gültigkeit dieser Identität kann am Einheitskreis gezeigt werden, mit Hilfe des Satzes von Pythagoras, der auch namensgebend für diesen häufig benutzten Satz der Trigonometrie ist.

Geometrische Herleitung

Als Grundlage dient der Satz des Pythagoras. Er besagt, dass in einem rechtwinkligen Dreieck mit der Hypotenuse und den Katheten und

$a^{2}+b^{2}=c^{2}$

gilt. Wird der Winkel $\alpha$ im besagten rechtwinkligen Dreieck so gewählt, dass seine Gegenkathete und seine Ankathete ist, so gilt allgemein

$a=\sin \alpha \cdot c$ ,

$b=\cos \alpha \cdot c$ .

Einsetzen beider Gleichungen in den Satz des Pythagoras ergibt dann

$(\sin^2 \alpha + \cos^2 \alpha) \cdot c^2 = c^2$ ,

$\sin^2 \alpha + \cos^2 \alpha = 1$ .

Geometrische Veranschaulichung

In der nebenstehenden Skizze sind der Einheitskreis, das heißt ein Kreis mit Radius 1, und ein rechtwinkliges Dreieck mit Hypotenusenlänge 1 im Einheitskreis dargestellt. Der Satz des Pythagoras gilt hier für einen beliebigen Wert des Winkels $\alpha$ im Einheitskreis und zeigt sofort die Gültigkeit des „trigonometrischen Pythagoras“.

Analytische Herleitung

Für stumpfe und überstumpfe Winkel $\alpha$ ist die Beweiskraft der Anschauung problematisch, da für solche (mindestens) eine Winkelfunktion negative Werte hat; was sind "negative Seiten" eines rechtwinkligen Dreiecks? Ein analytischer Beweis zeigt, dass der trigonometrische Pythagoras für beliebige reelle und komplexe Argumente $\alpha$ der verwendeten Winkelfunktionen gilt.

Mit der imaginären Einheit und der dritten binomischen Formel lässt sich faktorisieren:

$\cos ^{2}(\alpha )+\sin ^{2}(\alpha )=\cos ^{2}(\alpha )-\mathrm {i} ^{2}\cdot \sin ^{2}(\alpha )=(\cos(\alpha )+\mathrm {i} \cdot \sin(\alpha ))\cdot (\cos(\alpha )-\mathrm {i} \cdot \sin(\alpha ));$

da der Cosinus eine gerade Funktion und der Sinus eine ungerade Funktion ist, folgt mit der Eulerschen Formel weiter:

$(\cos(\alpha )+\mathrm {i} \cdot \sin(\alpha ))\cdot (\cos(\alpha )-\mathrm {i} \cdot \sin(\alpha ))=(\cos(\alpha )+\mathrm {i} \cdot \sin(\alpha ))\cdot (\cos(-\alpha )+\mathrm {i} \cdot \sin(-\alpha ))=\mathrm {e} ^{\mathrm {i} \alpha }\cdot \mathrm {e} ^{-\mathrm {i} \alpha }=\mathrm {e} ^{0}=1,\quad$ q.e.d.

Basierend auf einem Artikel in:

Wikipedia.de