
Binomische Formeln
Die binomischen Formeln sind in der elementaren Algebra verbreitete Formeln zum Umformen von Produkten aus Binomen. Sie werden als Merkformeln verwendet, die zum einen das Ausmultiplizieren von Klammerausdrücken erleichtern, zum anderen erlauben sie die Faktorisierung von Termen, also die Umformung von bestimmten Summen und Differenzen in Produkte, was bei der Vereinfachung von Bruchtermen, beim Radizieren von Wurzeltermen sowie Logarithmenausdrücken sehr oft die einzige Lösungsstrategie darstellt. Im Grunde sind sie Spezialfälle des Distributivgesetzes für algebraische Summen (jedes Glied der einen wird mit jedem der anderen Summe multipliziert)
mit ,
und den entsprechenden Vorzeichenvarianten.
Das Adjektiv binomisch leitet sich vom Substantiv Binom, also von bi (zwei) und Nomen (Namen) ab. Die binomischen Formeln gelten in allen kommutativen Ringen.
Formeln
Als binomische Formeln werden üblicherweise die folgenden drei Umformungen bezeichnet:
-
erste binomische Formel (Plus-Formel) zweite binomische Formel (Minus-Formel) dritte binomische Formel (Plus-Minus-Formel)
Die Gültigkeit der Formeln ist durch Ausmultiplizieren einzusehen:
Geometrische Veranschaulichung
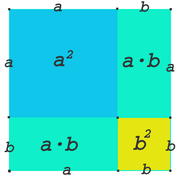 |
Das nebenstehende mehrfarbige Quadrat hat
die Seitenlänge
Dadurch ergibt sich |
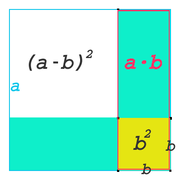 |
Im zweiten Bild ist Die hier gezeigte Formel lautet also |
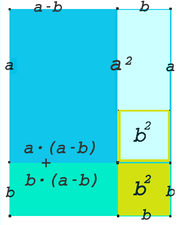 |
Im dritten Bild ist Also ergibt sich die Formel |
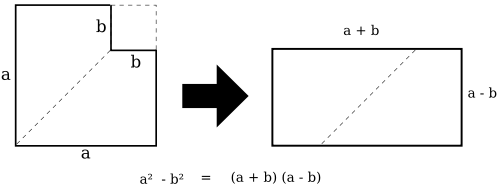
Eine weitere Veranschaulichung der dritten binomischen Formel erhält man durch folgende Zerlegung:
Bedeutung und Anwendungen
Tricks zum Kopfrechnen
Diese Formeln, häufig in der Mathematik benutzt, bieten auch eine Hilfe beim Kopfrechnen. Das Quadrat einer beliebigen Zahl zwischen 10 und 100 lässt sich oft einfach mit der binomischen Formel bestimmen, indem man die Berechnung auf Quadrate von einfacheren Zahlen (Vielfache von 10 oder einstellige Zahlen) zurückführt. Beispielsweise ist
oder
.
Bei Kenntnis der Quadratzahlen bis 20 lassen sich auch viele Multiplikationen auf die dritte binomische Formel zurückführen. Beispielsweise ist
.
Mit Hilfe der binomischen Formeln lassen sich Multiplikation und Division auf die einfacheren Rechenarten Quadrieren, Addieren, Subtrahieren, Halbieren und Verdoppeln zurückführen:
Die erste und zweite binomische Formel liefern für das Produkt
zweier Zahlen
und
:
Wer an Stelle des Einmaleins die ersten hundert Quadratzahlen kennt, kann so das allgemeine Produkt zweier Zahlen leicht berechnen. In Ermangelung eines Ziffernsystems mit Null haben nachweislich die Babylonier so gerechnet und in der ganzen Antike und im Mittelalter wird man so gerechnet haben. Die angebliche Umständlichkeit der antiken Zahlsysteme wird damit relativiert, da man mit diesen Zahlsystemen sehr gut addieren und subtrahieren konnte.
Addition und Subtraktion von Wurzeln
Die erste und zweite binomische Formel liefern auch ein
Rechenverfahren zur Addition bzw. Subtraktion von Wurzeln. Da
bzw.
nicht direkt berechenbar sind, quadriert man die Summe bzw. Differenz und zieht
anschließend aus dem Quadrat die Wurzel. Das Verfahren führt aber zu
Schachtelwurzeln, die nicht unbedingt einfacher sind als die ursprünglichen
Ausdrücke.
Da Wurzeln als nichtnegativ definiert und Quadrate von sich aus nie negativ sind, ist bei Differenzen von Wurzeln eine Fallunterscheidung nötig:
für
für
Potenzen von komplexen Zahlen (in arithmetischer Darstellung)
Die binomischen Formeln dienen auch zur Berechnung von Potenzen von komplexen Zahlen, wobei
für den Realteil,
für den Imaginärteil steht:
Aus der dritten binomischen Formel lässt sich auch eine Faktorisierung von
herleiten, indem man die Summe von Quadraten als Differenz schreibt:
.
Die dritte binomische Formel ist nicht nur ein Kopfrechenkniff,
sondern liefert auch ein Verfahren, die Division auf die Multiplikation und eine
einfachere Division zurückzuführen. Beispielsweise wird durch die Erweiterung
eines Bruches mit Nenner
mit dem so genannten konjugierten
der Nenner rational gemacht. Analog kann die Division durch komplexen (und hyperkomplexen)
Zahlen in eine Division durch reelle
Zahlen umgeformt werden.
Erweiterte Formeln 2. Grades
Aus den binomischen Formeln leiten sich einige spezielle Formeln ab, die auch für die Zahlentheorie eine gewisse Bedeutung haben:
- Babylonische Multiplikationsformel:
(s.o.)
- Formel für Pythagoräische
Tripel:
Beispiel:
liefert
.
- Identität von Diophant:
Beispiel:
liefert
.
- Brahmagupta-Identität:
Höhere Potenzen und Faktorisierungen von Potenzsummen
Binomische Formeln lassen sich auch für höhere Potenzen angeben, diese Verallgemeinerung ist der binomische Lehrsatz:
Dabei bezeichnen
die Binomialkoeffizienten,
die beispielsweise mittels des Pascalschen
Dreiecks leicht zu bestimmen sind. Die erste und die zweite binomische
Formel sind Spezialfälle des binomischen Lehrsatzes für
:
Für
ergibt sich z.B.
.
Eine Verallgemeinerung auf nicht notwendig natürliche Exponenten führt auf eine Potenzreihenentwicklung, die durch die binomische Reihe gegeben ist.
Auch zur dritten binomischen Formel gibt es eine Verallgemeinerung, die die
Faktorisierung von
ermöglicht:
oder allgemein für höhere natürliche Potenzen
Aus einem Ausdruck
lässt sich immer
abspalten; als Restpolynom erhält man eine Summe. Ist
eine Primzahl, ist dieses Restpolynom irreduzibel; weitere Zerlegungen sind nur
noch über die komplexen Zahlen möglich. Andernfalls lässt sich die Summe weiter
zerlegen, und ist
ein Produkt von 3 oder mehr verschiedenen ungeraden Primzahlen, entstehen auch
Polynome mit Koeffizienten ungleich 0, −1, +1. So entsteht bei der Zerlegung von
ein Polynom, beginnend mit
Mit
erhält man als Restpolynome die sog. Kreisteilungspolynome.
Bei geradem
lässt sich sogar stets
und damit auch
abspalten; bei der Division entsteht als Restpolynom eine alternierende
Summe:
für
Eine Faktorisierung von
ist ebenfalls möglich, wenn
ungerade ist. Auch hierbei entsteht eine alternierende Summe, diesmal mit einem
geraden Exponenten als höchstem und einem positiven Glied am Schluss,
z.B.:
Für gerade
ist eine Faktorisierung von
über die komplexen
Zahlen möglich, aber nur für
unumgänglich:
(s.o.)
Bereits
lässt sich mit Hilfe der Sophie-Germain-Identität in zwei quadratische Faktoren
mit reellen Koeffizienten aufspalten:
. Ebenso
Damit ist bei allen höheren geraden
eine Faktorisierung in Faktoren höherer Ordnung möglich, z.B.:
Nur bei einer weiteren Zerlegung beider irreduzibler Faktoren, etwa in Linearfaktoren, entstehen komplexe Koeffizienten.
Bemerkenswert ist auch die Faktorisierung von
bzw.
Die gar nicht triviale Zerlegung des Restpolynoms 4.Grades in zwei
quadratische Polynome findet ihre Anwendung bei der Lösung von Gleichungen
4.Grades. Die anderen Restpolynome
(s.o.) bzw.
sind dagegen irreduzibel.
Eine Division von
durch
ist grundsätzlich nicht ohne Rest möglich.
Erweiterungen auf mehrgliedrige Ausdrücke
Eine Verallgemeinerung der binomischen Formeln auf Potenzen von Polynomen, also von Summen mit mehr als zwei Gliedern, führt auf das Multinomialtheorem. Beispielsweise gilt für das Quadrat eines Trinoms
.
Die Koeffizienten sind in der Pascalschen Pyramide enthalten. So ist
Beispielanwendung


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 26.01. 2022