Mischverteilung
Der Begriff Mischverteilung oder zusammengesetzte Verteilung stammt aus der Wahrscheinlichkeitsrechnung. Es handelt sich dabei um die Wahrscheinlichkeitsverteilung der Mischung von Zufallsgrößen aus mehreren verschiedenen Grundgesamtheiten.
Einführendes Beispiel
Betrachtet man beispielsweise das Merkmal Körpergröße bei Kleinkindern (erste Grundgesamtheit) und Erwachsenen (zweite Grundgesamtheit), ist dieses Merkmal innerhalb jeder einzelnen Grundgesamtheit meist annähernd normalverteilt, wobei der Mittelwert für die Kleinkinder deutlich niedriger liegen dürfte als für die Erwachsenen. Die Mischverteilung ist nun die Verteilung der Körpergröße, wenn man die beiden Grundgesamtheiten Kleinkinder und Erwachsene nicht einzeln, sondern gemeinsam betrachtet, also die Verteilung der Körpergröße einer Person, von der man nicht weiß, ob sie Kleinkind oder Erwachsener ist.
Mathematisch handelt es sich in diesem Beispiel bei der Körpergröße der
Kleinkinder um eine Zufallsgröße
aus der einen Grundgesamtheit
und bei der Körpergröße der Erwachsenen um eine andere Zufallsgröße
aus der anderen Grundgesamtheit
.
Die Mischung dieser beiden Zufallsgrößen ist eine weitere Zufallsgröße
,
die mit einer gewissen Wahrscheinlichkeit
als
der ersten Grundgesamtheit
bzw. mit Wahrscheinlichkeit
als
der anderen Grundgesamtheit
entstammt. Da nur diese beiden Grundgesamtheiten zur Auswahl stehen, muss
gelten. Die Wahrscheinlichkeiten
und
lassen sich auch als relative Anteile der Grundgesamtheiten
und
an der gemeinsamen Grundgesamtheit interpretieren, bezogen auf das Beispiel also
als Anteil der Kleinkinder beziehungsweise der Erwachsenen an der
Gesamtstichprobe. Die Verteilung von
bestimmt sich über das Gesetz der
totalen Wahrscheinlichkeit zu
Wenn
und
Verteilungsfunktionen
und
haben, lautet die Verteilungsfunktion
von
also
.
Definition
Lässt sich die Dichtefunktion
einer stetigen
Zufallsvariablen
als
schreiben, so sagt man, dass
einer Mischverteilung folgt. Dabei sind die
Dichtefunktionen von stetigen Zufallsvariablen
und die
Wahrscheinlichkeiten mit
.
ist also eine Konvexkombination
der Dichten
.
Man kann leicht zeigen, dass unter diesen Bedingungen
nichtnegativ ist und die Normierungseigenschaft
erfüllt ist.
Entsprechend ergibt sich die Wahrscheinlichkeitsfunktion einer diskreten Mischverteilung als
aus den Wahrscheinlichkeitsfunktionen
von diskreten Zufallsvariablen
.
Eigenschaften
Für die Momente
von
gilt:
Dies folgt (im stetigen Fall) aus
Eine analoge Rechnung ergibt die Formel für den diskreten Fall.
Häufiger Spezialfall: Gaußsche Mischmodelle
Ein häufiger Spezialfall von Mischverteilungen sind sogenannte Gaußsche Mischmodelle
(gaussian mixture models, kurz: GMMs).
Dabei sind die Dichtefunktionen
die der Normalverteilung
mit potenziell verschiedenen Mittelwerten
und Standardabweichungen
(beziehungsweise Mittelwertvektoren und Kovarianzmatrizen
im
-dimensionalen
Fall). Es gilt also
und die Dichte
der Mischverteilung hat die Form
.
Parameterschätzung
Schätzer für die Parameter von Wahrscheinlichkeitsverteilungen werden häufig mit dem Maximum-Likelihood-Verfahren hergeleitet. Im Falle von Mischverteilungen ergeben sich dabei allerdings meist Gleichungen, deren Lösungen sich nicht algebraisch angeben lassen und daher numerisch bestimmt werden müssen. Ein typisches Verfahren dazu ist der Expectation-Maximization-Algorithmus (EM-Algorithmus), der beginnend bei initialen Werten für die Parameter eine Folge von immer besseren Schätzwerten erzeugt, die sich in vielen Fällen den realen Parametern annähern.
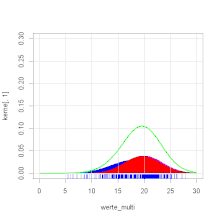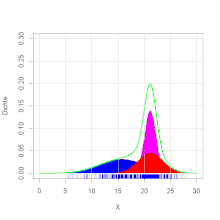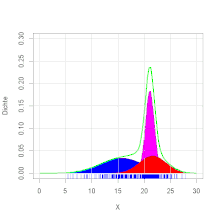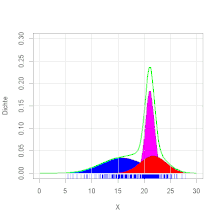
Beispiel
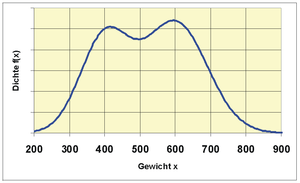
Ein Forellenzüchter verkauft Forellen in großen Mengen. Es wird im Herbst
beim Leeren der Teiche eine Bestandsaufnahme gemacht. Dabei werden die
herausgefischten Forellen gewogen. Es ergibt sich die Verteilung des Gewichts,
wie in der Grafik zu ersehen ist. Die Zweigipfligkeit der Verteilung deutet auf
eine Mischverteilung hin. Es stellt sich heraus, dass die Forellen aus zwei
verschiedenen Teichen stammen. Die Forellengewichte aus dem ersten Teich sind normalverteilt mit dem
Erwartungswert 400 g und
der Varianz
4900 g2 und die aus dem zweiten Teich mit dem Erwartungswert 600 g
und der Varianz 8100 g2. Aus dem ersten Teich stammen 40 % der
Forellen, aus dem zweiten 60 %. Es ergibt sich die Dichtefunktion
(siehe Abbildung).
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 09.04. 2023