F-Verteilung

Die F-Verteilung oder Fisher-Verteilung, auch Fisher-Snedecor-Verteilung (nach Ronald Aylmer Fisher und George W. Snedecor), ist eine stetige Wahrscheinlichkeitsverteilung. Eine F-verteilte Zufallsvariable ergibt sich als Quotient zweier jeweils durch die zugehörige Anzahl der Freiheitsgrade geteilter Chi-Quadrat-verteilter Zufallsvariablen. Die F-Verteilung besitzt zwei unabhängige Freiheitsgrade als Parameter und bildet so eine Zwei-Parameter-Verteilungsfamilie.

Die F-Verteilung wird häufig in einem Test verwendet (F-Test), um festzustellen, ob der Unterschied zweier Stichprobenvarianzen auf statistischer Schwankung beruht oder ob er auf unterschiedliche Grundgesamtheiten hinweist. Auch im Rahmen der Varianzanalyse wird mit einer F-Statistik auf signifikante Unterschiede zwischen Grundgesamtheiten (Gruppen) getestet.

Definition

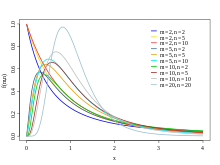
Dichtefunktion der F-Verteilung mit ausgewählten Freiheitsgraden und

Verteilungsfunktion der F-Verteilung mit ausgewählten Freiheitsgraden und

Eine stetige Zufallsvariable genügt der F-Verteilung F(m,n) , mit Freiheitsgraden im Zähler und Freiheitsgraden im Nenner, wenn sie die Wahrscheinlichkeitsdichte

$f(x\mid m,n)=m^{\frac {m}{2}}n^{\frac {n}{2}}\cdot {\frac {\Gamma ({\frac {m+n}{2}})}{\Gamma ({\frac {m}{2}})\Gamma ({\frac {n}{2}})}}\cdot {\frac {x^{{\frac {m}{2}}-1}}{(mx+n)^{\frac {m+n}{2}}}},\quad x>0$

besitzt. Dabei ist mit $\Gamma (x)$ die Gammafunktion an der Stelle bezeichnet.

Historisch bildet die nachfolgende Definition den Ursprung der F-Verteilung als die Verteilung der Größe

$F_{{m,n}}={\frac {\chi _{m}^{2}/m}{\chi _{n}^{2}/n}},$

wobei $\chi _{m}^{2}$ und $\chi_n^2$ unabhängige, Chi-Quadrat-verteilte Zufallsvariablen mit bzw. Freiheitsgraden sind.

Eigenschaften

Erwartungswert

Der Erwartungswert existiert nur für n>2 und hat dann den Wert

$\operatorname {E}(F_{{m,n}})={\frac {n}{n-2}}$ .

Varianz

Die Varianz ist nur für n>4 definiert und lautet dann

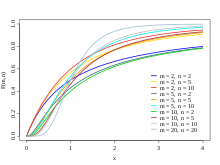
$\operatorname {Var}(F_{{m,n}})={\frac {2n^{2}(m+n-2)}{m(n-2)^{2}(n-4)}}$ .

Verteilungsfunktion

Die Werte der Verteilung $P(X\leq x)=F(x|m;n)$ werden meist numerisch ermittelt und in einer Tabelle angegeben. Eine komplette Tabellierung bezüglich aller Freiheitsgrade ist i.A. nicht notwendig, sodass die meisten Verteilungstabellen die Quantile bezüglich ausgewählter Freiheitsgrade und Wahrscheinlichkeiten angeben. Man macht sich hier auch die Beziehung zunutze:

$F^{-1}(p;m;n)={\frac {1}{F^{-1}(1-p;n;m)}},$

wobei $F^{{-1}}(p;m;n)$ das -Quantil der F-Verteilung mit und Freiheitsgraden bedeutet.

Die F-Verteilung lässt sich geschlossen ausdrücken als

$F(x|m;n)=I\left({\frac {m\cdot x}{m\cdot x+n}},{\frac {m}{2}},{\frac {n}{2}}\right),$

wobei $I(z,a,b)={\frac {1}{B(a,b)}}\cdot \int _{0}^{z}t^{a-1}(1-t)^{b-1}\mathrm {d} t$ die regularisierte unvollständige Betafunktion darstellt.

Maximum

Für m>2 nimmt an der Stelle

$x_{{{\mathrm {max}}}}={\frac {n(m-2)}{m(n+2)}}$

das Maximum an.

Entropie

Die Entropie der F-Verteilung (ausgedrückt in nats) beträgt

$H(X)=\ln \left({\frac {n}{m}}\cdot {\frac {\Gamma \left({\frac {m}{2}}\right)\Gamma \left({\frac {n}{2}}\right)}{\Gamma \left({\frac {m}{2}}+{\frac {n}{2}}\right)}}\right)+\left(1-{\frac {m}{2}}\right)\psi \left({\frac {m}{2}}\right)-\left(1+{\frac {n}{2}}\right)\psi \left({\frac {n}{2}}\right)+{\frac {m+n}{2}}\psi \left({\frac {m+n}{2}}\right),$

wobei $\psi$ die Digamma-Funktion bezeichnet.

Beziehungen zu anderen Verteilungen

Das Zeichen $\sim$ bedeutet im Folgenden „ist verteilt wie“.

Beziehung zur Beta-Verteilung

Die Zufallsvariable

$Y={\frac {{\frac {m}{n}}F_{m,n}}{1+{\frac {m}{n}}F_{m,n}}}$

ist betaverteilt mit Parametern m/2 und n/2 $\left(Y\sim \operatorname {Beta}(m/2,n/2)\right).$ Es gilt:

$Y\sim {\frac {\chi _{m}^{2}}{\chi _{m}^{2}+\chi _{n}^{2}}}$

wobei $\chi _{m}^{2}$ und $\chi_n^2$ unabhängige Chi-Quadrat-verteilte Zufallsgrößen sind mit bzw. Freiheitsgraden.

Beziehung zur Chi-Quadrat-Verteilung

Aus den unabhängigen $\chi _{m}^{2}$ und $\chi_n^2$ Chi-Quadrat-verteilten Zufallsgrößen mit bzw. Freiheitsgraden lässt sich

$F_{{m,n}}={\frac {\chi _{m}^{2}/m}{\chi _{n}^{2}/n}}$

konstruieren. Diese Zufallsvariable ist F(m,n) -verteilt.

Beziehung zur nichtzentralen F-Verteilung

Für unabhängige Zufallsvariablen $X\sim \chi ^{2}(\delta ,m)$ und $Y\sim \chi ^{2}(n)$ ist

$Z={\frac {X/m}{Y/n}}$

verteilt nach der nichtzentralen F-Verteilung $Z\sim F(\delta ,m,n)$ mit Nichtzentralitäts-Parameter $\delta$ . Dabei ist $\chi ^{2}(\delta ,\,m)$ eine nichtzentrale Chi-Quadrat-Verteilung mit Nichtzentralitäts-Parameter $\delta$ und Freiheitsgraden. Für $\delta =0$ ergibt sich die zentrale F-Verteilung $F(m,\,n)$ .

Dichte der nichtzentralen F-Verteilung

$g(z|m,n,\delta )=f(z|m,n)\cdot e^{{-\delta /2}}{}_{1}{\mathcal F}_{1}\left({\frac {m+n}{2}},{\frac m2},{\frac {m\cdot z\cdot \delta }{2(m\cdot z+n)}}\right).$

Die Funktion ${}_{1}{\mathcal F}_{1}(a,b,x)$ ist eine spezielle hypergeometrische Funktion, auch Kummersche Funktion genannt und f(x|m,n) repräsentiert die oben angegebene Dichte der zentralen F-Verteilung.

Erwartungswert und Varianz der nichtzentralen F-Verteilung sind gegeben durch

${\frac {n(1+\delta /m)}{n-2}}$ mit n>2

und

${\frac {2n^{2}(m(1+\delta /m)^{2}+(n-2)(1+2\delta /m))}{m(n-2)^{2}(n-4)}}$ mit $n>4.$

Beide ergeben bei $\delta \to 0$ die Formeln der zentralen F-Verteilung.

Beziehung zur Normalverteilung

Wenn die unabhängigen normalverteilten Zufallsvariablen $X_{1},X_{2},\dotsc ,X_{m},Y_{1},Y_{2},\dotsc ,Y_{n}$ die Parameter

$\operatorname {E} (X_{i})=\mu ,\quad \operatorname {Var} (X_{i})=\sigma ^{2}$

$\operatorname {E} (Y_{j})=\nu ,\quad \operatorname {Var} (Y_{j})=\tau ^{2}$

besitzen, sind die jeweiligen Stichprobenvarianzen $S_{X}^{2}$ und $S_{Y}^{2}$ unabhängig, und es gilt:

${\frac {S_{X}^{2}}{\sigma ^{2}}}\sim \chi _{{m-1}}^{2}/(m-1)$

${\frac {S_{Y}^{2}}{\tau ^{2}}}\sim \chi _{{n-1}}^{2}/(n-1)$

Deshalb unterliegt die Zufallsvariable

$F={\frac {S_{X}^{2}/\sigma ^{2}}{S_{Y}^{2}/\tau ^{2}}}$

einer F-Verteilung mit m-1 Freiheitsgraden im Zähler und n-1 Freiheitsgraden im Nenner.

Beziehung zur Studentschen t-Verteilung

Wenn $X\sim t_{n}$ (Studentsche t-Verteilung), dann ist $X^{2}\sim F(1,n).$

Das Quadrat einer t-verteilten Zufallsvariablen mit Freiheitsgraden folgt einer F-Verteilung mit m=1 und Freiheitsgraden.

Herleitung der Dichte

Die Wahrscheinlichkeitsdichte der F-Verteilung lässt sich herleiten (vgl. Herleitung der Dichte der Studentschen t-Verteilung) aus der gemeinsamen Dichte der beiden unabhängigen Zufallsvariablen $\chi _{m}^{2}$ und $\chi^2_n$ , die beide Chi-Quadrat-verteilt sind.

$g_{\chi _{m}^{2},\chi _{n}^{2}}(x,y)=\left({\frac {1}{2^{\frac {m}{2}}\Gamma ({\tfrac {m}{2}})}}x^{{\frac {m}{2}}-1}\operatorname {exp} \left\{-{\frac {x}{2}}\right\}\right)\cdot \left({\frac {1}{2^{\frac {n}{2}}\Gamma ({\tfrac {n}{2}})}}y^{{\frac {n}{2}}-1}\operatorname {exp} \left\{-{\frac {y}{2}}\right\}\right)$ .

Mit der Transformation

$f={\frac {x/m}{y/n}},v=y$

bekommt man die gemeinsame Dichte von $F={\frac {\chi _{m}^{2}/m}{\chi _{n}^{2}/n}}$ und $\chi^2_n$ , wobei $f\geq 0$ und $v\geq 0$ gilt.

Die Jacobideterminante dieser Transformation ist:

$\det {\frac {\partial (x,y)}{\partial (f,v)}}={\begin{vmatrix}{\frac mn}v&0\\\Diamond &1\end{vmatrix}}={\frac mn}v$

Der Wert $\Diamond$ ist unwichtig, weil er bei der Berechnung der Determinante mit 0 multipliziert wird. Die neue Dichtefunktion schreibt sich also

$g_{{F,\chi _{n}^{2}}}(f,v)={\frac {1}{2^{{\frac m2}}\Gamma ({\frac m2})}}\left(fv\,{\frac mn}\right)^{{{\frac {m}{2}}-1}}e^{{-{\frac 12}(fv\,{\frac mn})}}\cdot {\frac {1}{2^{{\frac n2}}\Gamma ({\frac n2})}}v^{{{\frac {n}{2}}-1}}e^{{-{\frac 12}v}}\cdot {\frac {m}{n}}v.$

Gesucht ist nun die Randverteilung $g_{{m,\,n}}(f)$ als Integral über die nicht interessierende Variable :

$g_{m,n}(f)=\int \limits _{0}^{\infty }g_{F,\chi _{n}^{2}}(f,v)\,dv={\frac {({\frac {m}{n}})^{\frac {m}{2}}f^{{\frac {m}{2}}-1}}{2^{\frac {m+n}{2}}\Gamma ({\frac {m}{2}})\Gamma ({\frac {n}{2}})}}\int \limits _{0}^{\infty }v^{{\frac {m+n}{2}}-1}e^{-{\frac {v}{2}}(1+{\frac {m}{n}}f)}\,dv=m^{\frac {m}{2}}n^{\frac {n}{2}}\cdot {\frac {\Gamma ({\frac {m}{2}}+{\frac {n}{2}})}{\Gamma ({\frac {m}{2}})\Gamma ({\frac {n}{2}})}}\cdot {\frac {f^{{\frac {m}{2}}-1}}{(mf+n)^{\frac {m+n}{2}}}}.$

Quantilfunktionen

Das -Quantil der F-Verteilung x_p ist die Lösung der Gleichung $p=F(x_p|m,\,n)$ und damit prinzipiell über die Umkehrfunktion zu berechnen. Konkret gilt hier

$x_{p}={\frac {nI^{-1}(p,{\frac {m}{2}},{\frac {n}{2}})}{m(1-I^{-1}(p,{\frac {m}{2}},{\frac {n}{2}}))}}$

mit $I^{{-1}}$ als Inverse der regularisierten unvollständigen Betafunktion. Dieser Wert x_p ist in der F-Verteilungstabelle unter den Koordinaten , und eingetragen .

Für einige Werte , lassen sich die Quantilsfunktionen $x_{p}(m,\,n)$ explizit ausrechnen. Man löst das Beta-Integral $I({\tfrac {mx}{mx+n}},{\tfrac {m}{2}},{\tfrac {n}{2}})$ mit $m,n=1,2,\dotsc ,$ wobei für ein paar Indizes invertierbare Funktionen auftreten:

${\begin{array}{c|c|c|c|c}m\downarrow ,\,n\rightarrow &1&2&3&4\\\hline 1&\tan({\frac {\pi }{2}}p)^{2}&{\frac {2p^{2}}{1-p^{2}}}&?&{\frac {4}{2\cos({\frac {2\arcsin(p)}{3}})-1}}-4\\\hline 2&{\frac {1}{2}}({\frac {1}{(1-p)^{2}}}-1)&{\frac {p}{1-p}}&{\frac {3}{2}}({\frac {1}{(1-p)^{2/3}}}-1)&{\frac {2}{\sqrt {1-p}}}-2\\\hline 3&?&{\frac {2p^{2/3}}{3-3p^{2/3}}}&?&?\\\hline 4&{\frac {1}{(4\sin({\frac {\arcsin(1-p)}{3}}))^{2}}}-{\frac {1}{4}}&{\frac {\sqrt {p}}{2(1-{\sqrt {p}})}}&?&{\frac {1}{{\frac {1}{2}}+\sin({\frac {\arcsin(1-2p)}{3}})}}-1\\\end{array}}$

Aus der jeweils vollständigen Zeile und Spalte kann man sogar die allgemeinen Ausdrücke für höhere Indizes ablesen. Man findet:

$x_{p}(2,\,n)={\frac {n}{2}}\left({\frac {1}{(1-p)^{2/n}}}-1\right)$

$x_{p}(m,\,2)={\frac {2}{m}}\left({\frac {p^{2/m}}{1-p^{2/m}}}\right)$

Siehe auch

Fishersche z-Verteilung

Basierend auf einem Artikel in:

Wikipedia.de