Bestimmtheitsmaß

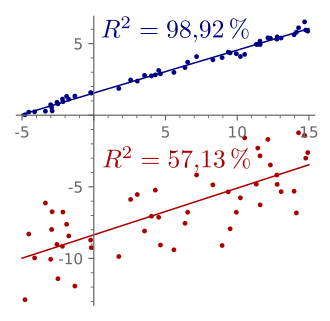
Dieses Streudiagramm zeigt zwei konkrete empirische Regressionsgeraden einer linearen Einfachregression, die jeweils bestmöglich durch die „Punktwolke“ der Messung gelegt wurden. Zu erkennen ist, dass die obere Gerade eine bessere Anpassung an die Daten liefert als die untere. Formal lässt sich dies anhand eines höheren R-Quadrat-Wertes erkennen ( ${\mathit {R}}^{2}=98{,}92\,\%$ vs. ${\mathit {R}}^{2}=57{,}13\,\%$ ).

Das Bestimmtheitsmaß, auch Determinationskoeffizient (von lateinisch determinatio „Abgrenzung, Bestimmung“ bzw. determinare „eingrenzen“, „festlegen“, „bestimmen“ und coefficere „mitwirken“), bezeichnet mit ${\mathit {R}}^{2}$ , ist in der Statistik eine Kennzahl zur Beurteilung der Anpassungsgüte einer Regression – beispielsweise, um zu bewerten, wie gut Messwerte zu einem Modell passen. Das Bestimmtheitsmaß beruht auf der Quadratsummenzerlegung, bei der die totale Quadratsumme in die (durch das Regressionsmodell) erklärte Quadratsumme und in die Residuenquadratsumme zerlegt wird.

In der einfachen und multiplen linearen Regression ist das Bestimmtheitsmaß definiert als „der Anteil der durch die Regression erklärten Quadratsumme an der zu erklärenden totalen Quadratsumme“ und gibt an, wie viel Streuung in den Daten durch ein vorliegendes lineares Regressionsmodell „erklärt“ werden kann. Das Bestimmtheitsmaß entspricht bei der einfachen linearen Regression und der multiplen linearen Regression genau dem Quadrat des Bravais-Pearson-Korrelationskoeffizienten. Ansonsten existieren unterschiedliche Definitionen, wie zum Beispiel bei den Pseudo-Bestimmtheitsmaßen. Das Bestimmtheitsmaß steht in enger Beziehung zu weiteren Modellgütemaßen zur Prüfung der Regressionsfunktion, wie z.B zum Standardfehler der Regression und zur F-Statistik. Weil das Bestimmtheitsmaß durch die Aufnahme zusätzlicher Variablen wächst und die Gefahr der Überanpassung besteht, wird für praktische Anwendungen meist das adjustierte Bestimmtheitsmaß verwendet. Das adjustierte Bestimmtheitsmaß „bestraft“ im Gegensatz zum unadjustierten Bestimmtheitsmaß die Aufnahme jeder neu hinzugenommenen erklärenden Variable.

Obwohl das Bestimmtheitsmaß die am häufigsten benutzte Kennzahl ist, um die globale Anpassungsgüte einer Regression zu quantifizieren, wird es oft fehlinterpretiert und falsch angewendet, auch da bei einer Regression durch den Ursprung zahlreiche alternative Definitionen des Bestimmtheitsmaßes nicht äquivalent sind. Das Bestimmtheitsmaß ist ein reines Zusammenhangsmaß. So ist es nicht möglich das Bestimmtheitsmaß zu verwenden, um einen direkten kausalen Zusammenhang zwischen den Variablen nachzuweisen. Außerdem zeigt das Bestimmtheitsmaß nur die Größe des Zusammenhangs zwischen den Variablen, aber nicht, ob dieser Zusammenhang statistisch signifikant ist.

Einführung in die Problemstellung

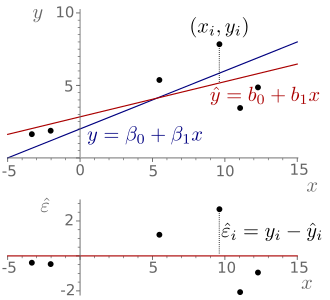
Regressiongerade ${\hat {y}}$ als Schätzer (Modellfunktion) für den Zusammenhang von Größe und Gewicht der Probanden. ${\hat {y}}(x_{i})={\hat {y}}_{i}$ ist das geschätzte Gewicht des Probanden bei einer gegebenen Größe $x_{i}$ . Der Restfehler (das Residuum) ${\hat {\varepsilon }}_{i}$ stellt die Differenz zwischen dem Messwert $y_{i}$ und Schätzwert $\hat{y}_i$ dar.

Gegeben sind Messungen $(x_{1},y_{1}),(x_{2},y_{2}),\ldots ,(x_{n},y_{n})$ , d.h. bei dem -ten Wertepaar (x_i,y_i) wird einem Wert $x_{i}$ (zB. Größe einer Person) ein Messwert $y_{i}$ (z.B. das gemessene Gewicht der Person) zugeordnet. Dazu berechnet man den empirischen Mittelwert $\textstyle {\overline {y}}={\frac {1}{n}}\sum _{i=1}^{n}y_{i}$ (z.B. das mittlere Gewicht der Probanden). Ferner gibt es einen Schätzer ${\hat {y}}$ (Modellfunktion), der jedem Wert $x_{i}$ (z.B. Größe) einen Schätzwert ${\hat {y}}(x_{i})\equiv {\hat {y}}_{i}$ (geschätztes Gewicht für eine Person mit Größe $x_{i}$ ) zuordnet. Die Abweichung einer Schätzung ${\hat {y}}(x_{i})$ von der zugehörigen Messung $y_{i}$ ist durch ${\hat {\varepsilon }}_{i}\equiv y_{i}-{\hat {y}}(x_{i})=y_{i}-{\hat {y_{i}}}$ gegeben und wird „Residuum“ genannt. Bei der einfachen linearen Regression, die zum Ziel hat, das Absolutglied (englisch intercept) $\beta _{0}$ , die Steigung (englisch slope) $\beta _{1}$ und die Störgrößenvarianz $\sigma ^{2}$ zu schätzen, wird der Schätzer anschaulich durch die Regressionsgerade beschrieben und mathematisch durch die Stichproben-Regressionsfunktion ${\hat {y}}={\hat {y}}(x)=b_{0}+b_{1}x$ definiert. Die beiden Parameterschätzer $b_{0}$ und $b_{1}$ werden auch als Kleinste-Quadrate-Schätzer bezeichnet.^{[A
1]} Wenn das zugrundeliegende Modell ein von Null verschiedenes Absolutglied $\beta _{0}$ enthält, stimmt der empirische Mittelwert der Schätzwerte $\hat{y}_i$ mit dem der beobachteten Messwerte $y_{i}$ überein, also $\textstyle {\overline {\hat {y}}}={\tfrac {1}{n}}\sum \nolimits _{i=1}^{n}{\hat {y_{i}}}={\overline {y}}$ (für einen Beweis siehe Abschnitt Matrixschreibweise).

Es empfiehlt sich, nach der Schätzung der Regressionsparameter die Regressionsgerade gemeinsam mit den Datenpunkten in ein Streudiagramm einzuzeichnen. Auf diese Weise bekommt man eine Vorstellung davon, wie „gut“ die Punkteverteilung durch die Regressionsgerade wiedergegeben wird. Je enger die Datenpunkte um die Regressionsgerade herum konzentriert sind, d.h. je kleiner also die Residuenquadrate sind, desto „besser“. In diesem Zusammenhang ist allerdings zu beachten, dass die Residuenquadrate typischerweise klein sind, wenn die abhängige Variable eine geringe Variabilität aufweist. Die geforderte Kleinheit der Residuenquadrate muss also in Relation zur Streuung der abhängigen Variablen betrachtet werden.

Ein Maß zur Beurteilung der Anpassungsgüte sollte außerdem die Streuung der Messwerte und die der geschätzten Werte in Relation setzen. Die Streuung der jeweiligen Werte um ihren Mittelwert kann mithilfe der „Summe der Abweichungsquadrate“ (Summe der Quadrate bzw. englisch Sum of Squares, kurz: SQ oder SS) gemessen werden. Das „mittlere Abweichungsquadrat“ stellt die empirische Varianz dar. Die Streuung der Schätzwerte $\hat{y}_i$ um ihren Mittelwert ${\overline {\hat {y}}}={\overline {y}}$ kann durch $SQE\equiv \sum \nolimits _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}$ gemessen werden und die Streuung der Messwerte $y_{i}$ um das Gesamtmittel $\overline {y}$ kann durch $\textstyle SQT\equiv \sum \nolimits _{i=1}^{n}(y_{i}-{\overline {y}})^{2}$ gemessen werden. Erstere stellt die durch die Regression „erklärte Quadratsumme“ (Summe der Quadrate der Erklärten Abweichungen bzw. englisch Sum of Squares Explained, kurz: SQE oder SSE) und letztere stellt die „zu erklärende Quadratsumme“ bzw. die „totale Quadratsumme“ (Summe der Quadrate der Totalen Abweichungen bzw. englisch Sum of Squares Total, kurz: SQT oder SST) dar. Das Verhältnis dieser beiden Größen wird das Bestimmtheitsmaß der Regression genannt (für die Berechnung des Bestimmtheitsmaßes zum Körpergröße-Körpergewicht-Beispiel mittels statistischer Software, siehe Bestimmtheitsmaß in R). Das Bestimmtheitsmaß zeigt, wie gut die durch die Schätzung gefundene Modellfunktion zu den Daten passt, d.h. wie gut sich die konkrete empirische Regressionsgerade einer angenommenen wahren Gerade $y=\beta _{0}+\beta _{1}x$ annähert. Die durch die Regression „nicht erklärten Abweichungen“ (Restabweichungen), d.h. die Abweichungen der Datenpunkte von der Regressionsgeraden werden durch die Regression „nicht erklärte Quadratsumme“ bzw. die Residuenquadratsumme (Summe der Quadrate der Restabweichungen (oder: „Residuen“) bzw. englisch Sum of Squares Residual, kurz: SQR oder SSR) erfasst, die durch $\textstyle SQR\equiv \sum \nolimits _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}$ gegeben ist.^{[A 2]}

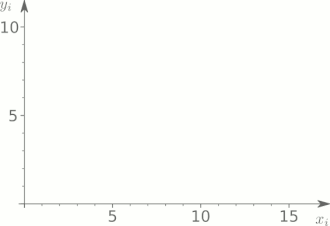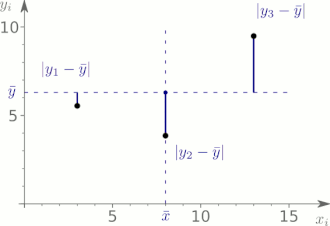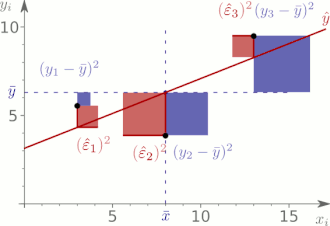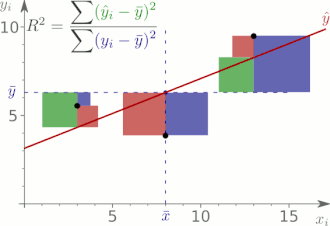
Das Bestimmtheitsmaß

Definition

Das Bestimmtheitsmaß der Regression, auch empirisches Bestimmtheitsmaß,^{[A
3]} ist eine dimensionslose Maßzahl die den Anteil der Variabilität in den Messwerten der abhängigen Variablen ausdrückt, der durch lineare Modell „erklärt“ wird. Gegeben die Quadratsummenzerlegung ist das Bestimmtheitsmaß der Regression definiert als das Verhältnis der durch die Regression erklärten Quadratsumme zur totalen Quadratsumme:^{[A 4]}

${\mathit {R}}^{2}\equiv {\frac {SQE}{SQT}}={\frac {\displaystyle \sum \nolimits \left({\hat {y}}_{i}-{\overline {y}}\right)^{2}}{\displaystyle \sum \nolimits \left(y_{i}-{\overline {y}}\right)^{2}}}=1-{\frac {SQR}{SQT}}=1-{\frac {\displaystyle \sum \nolimits \left(y_{i}-{\hat {y}}_{i}\right)^{2}}{\displaystyle \sum \nolimits \left(y_{i}-{\overline {y}}\right)^{2}}}$ ,

wobei angenommen wird, dass für die totale Quadratsumme $SQT\neq 0$ gilt. Dies ist praktisch immer erfüllt, außer für den Fall, dass die Messwerte der abhängigen Variable keinerlei Variabilität aufweisen, d.h. $y_{1}=y_{2}=\ldots =y_{n}={\overline {y}}$ . In diesem Falle ist das Bestimmtheitsmaß nicht definiert. Die zweite Gleichheit, die sich mithilfe der Quadratsummenzerlegung zeigen lässt, ist eine alternative Berechnungsformel für das Bestimmtheitsmaß. Die alternative Berechnungsformel setzt die geforderte Kleinheit der Residuenquadrate in Relation zur gesamten Quadratsumme. Die zur Konstruktion des Bestimmtheitsmaßes verwendete Quadratsummenzerlegung kann als „Streuungszerlegung“ interpretiert werden, bei der die „Gesamtstreuung“ in die „erklärte Streuung“ und die „Reststreuung“ zerlegt wird.^{[A
5]} Das Bestimmtheitsmaß ist als gerade als jener Anteil der Gesamstreuung $SQT$ zu deuten, der mit der Regressionsfunktion erklärt werden kann. Der unerklärte Teil bleibt als Reststreuung zurück.

Das Bestimmtheitsmaß dient als Maßzahl zur Beurteilung der globalen Anpassungsgüte eines Regressionsmodells. In der einfachen linearen Regression und der multiplen linearen Regression entspricht das Bestimmtheitsmaß dem Quadrat des Bravais-Pearson-Korrelationskoeffizienten $r_{xy}$ (siehe auch Abschnitt Als quadrierter Korrelationskoeffizient). Dieser Umstand ist dafür verantwortlich, dass das Bestimmtheitsmaß als ${\mathit {R}}^{2}$ (lies: R Quadrat) oder $r^{2}$ notiert wird. In deutschsprachiger Literatur findet sich auch der Buchstabe als Bezeichnung für das Bestimmtheitsmaß. In den Anfängen der Statistik wurde mit dem Buchstaben ${\mathit {R}}$ ein Schätzer des Korrelationskoeffizienten der Grundgesamtheit notiert und in der Regressionsanalyse wird diese Notation noch heute verwendet.

Eigenschaften

Wertebereich des Bestimmtheitsmaßes

Mithilfe der obigen Definition können die Extremwerte für das Bestimmtheitsmaß aufgezeigt werden. Für das Bestimmtheitsmaß gilt, dass es umso näher am Wert ist, je kleiner die Residuenquadratsumme ist. Es wird maximal gleich , wenn $\textstyle \sum \nolimits _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}=0$ ist, also alle Residuen null sind. In diesem Fall ist die Anpassung an die Daten perfekt, was bedeutet, dass für jede Beobachtung $y_{i}={\hat {y}}_{i}$ ist und alle Beobachtungspunkte des Streudiagramms auf der Regressionsgeraden liegen. Das Bestimmtheitsmaß nimmt hingegen den Wert $0$ an, wenn $\textstyle \sum \nolimits _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}=0$ beziehungsweise $\textstyle \sum \nolimits _{i=1}^{n}(y_{i}-{\overline {y}})^{2}=\sum \nolimits _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}$ ist. Diese Gleichung besagt, dass die „nicht erklärte Streuung“ der „gesamten zu erklärenden Streuung“ entspricht und die erklärenden Variablen $x_1, x_2, \ldots , x_n$ somit keinen Beitrag zur Erklärung der Gesamtstreuung leisten. Die gesamte zu erklärende Streuung wird in diesem Fall durch die Residuen hervorgerufen und die Regressionsgleichung „erklärt“ gar nicht. Aus der Betrachtung dieser beiden Fälle folgt $0\leq {\mathit {R}}^{2}\leq 1$ . Wenn das Regressionsmodell kein Absolutglied enthält (es liegt ein homogenes Regressionsmodell vor), kann das Bestimmtheitsmaß negativ werden (siehe Abschnitt Einfache lineare Regression durch den Ursprung). Ebenfalls kann das Bestimmtheitsmaß negativ werden, wenn es auf simultane Gleichungsmodelle angewendet wird, da in diesem Kontext ${\overline {\hat {y}}}$ nicht notwendigerweise gleich $\overline {y}$ ist.

Als quadrierter Korrelationskoeffizient

Bei einer einfachen linearen Regression (nur eine erklärende Variable) $y_{i}=\beta _{0}+x_{i}\beta _{1}+\varepsilon _{i}$ entspricht das Bestimmtheitsmaß dem Quadrat des Bravais-Pearson-Korrelationskoeffizienten $r_{xy}$ und lässt sich aus der Produktsumme $SP_{xy}$ (Summe der Produkte der Abweichungen der Messwerte vom jeweiligen Mittelwert $(x_{i}-{\overline {x}})(y_{i}-{\overline {y}})$ ) und den Quadratsummen $SQ_{x}$ und $SQ_{y}$ berechnen:

${\mathit {R}}^{2}={\frac {\displaystyle \sum \nolimits _{i=1}^{n}({\hat {y}}_{i}-{\overline {\hat {y}}})^{2}}{\displaystyle \sum \nolimits _{i=1}^{n}\left(y_{i}-{\overline {y}}\right)^{2}}}={\frac {b_{1}^{2}\displaystyle \sum \nolimits _{i=1}^{n}\left(x_{i}-{\overline {x}}\right)^{2}}{\displaystyle \sum \nolimits _{i=1}^{n}\left(y_{i}-{\overline {y}}\right)^{2}}}=\left({\frac {SP_{xy}}{SQ_{x}}}\right)^{2}\cdot {\frac {SQ_{x}}{SQ_{y}}}=\left({\frac {SP_{xy}}{\sqrt {SQ_{x}SQ_{y}}}}\right)^{2}=r_{xy}^{2}$ ,

wobei der Kleinste-Quadrate-Schätzer für die Steigung $b_{1}=SP_{xy}/SQ_{x}$ der Quotient aus Produktsumme von und und Quadratsumme von ist. In der einfachen linearen Regression ist ${\mathit {R}}^{2}=0$ , wenn $b_{1}=0$ ist, d.h. die erklärende Variable steht zur Schätzung von nicht zur Verfügung. Dies folgt aus der Tatsache, dass in der einfachen linearen Regression $SQE=b_{1}^{2}\cdot SQ_{x}$ ^{[A
6]} gilt. In diesem Fall besteht das „beste“ lineare Regressionsmodell nur aus dem Absolutglied $b_{0}$ . Das so definierte Bestimmtheitsmaß ist ebenfalls gleich null, wenn der Korrelationskoeffizient $r_{xy}$ gleich null ist, da es in der einfachen linearen Regression dem quadrierten Korrelationskoeffizienten zwischen und entspricht. Im Kontext der einfachen linearen Regression wird das Bestimmtheitsmaß auch als einfaches Bestimmtheitsmaß bezeichnet. Bei der Interpretation des einfachen Bestimmtheitsmaßes muss man vorsichtig sein, da es u.U. schon deshalb groß ist, weil die Steigung $b_{1}$ der Regressionsgeraden groß ist.

In der Realität hängen abhängige Variablen im Allgemeinen von mehr als einer erklärenden Variablen ab. Zum Beispiel ist das Gewicht eines Probanden nicht nur von dessen Alter, sondern auch von dessen sportlicher Betätigung und psychologischen Faktoren abhängig. Bei einer multiplen Abhängigkeit gibt man die Annahme der einfachen linearen Regression auf, bei der die abhängige Variable nur von einer erklärenden Variablen abhängt. Um eine mehrfache Abhängigkeit zu modellieren, benutzt man ein typisches multiples lineares Regressionsmodell

$y_{i}=\beta _{0}+x_{i1}\beta _{1}+x_{i2}\beta _{2}+\dotsc +x_{ik}\beta _{k}+\varepsilon _{i}=\mathbf {x} _{i}^{\top }{\boldsymbol {\beta }}+\varepsilon _{i}$ .

Hierbei ist $p=k+1$ die Anzahl der zu schätzenden unbekannten Parameter und die Anzahl der erklärenden Variablen. Zusätzlich zur Dimension der unabhängigen Variablen wird auch eine zeitliche Dimension integriert, wodurch sich ein lineares Gleichungssystem ergibt, was sich in Vektor-Matrix-Form darstellen lässt.

Im Gegensatz zur einfachen linearen Regression entspricht in der multiplen linearen Regression das ${\mathit {R}}^{2}$ dem Quadrat des Korrelationskoeffizienten zwischen den Messwerten $y_{i}$ und den Schätzwerten $\hat{y}_i$ (für einen Beweis, siehe Matrixschreibweise), also

${\mathit {R}}^{2}={\frac {\left[\sum _{i=1}^{n}(y_{i}-{\overline {y}})({\hat {y}}_{i}-{\overline {y}})\right]^{2}}{\left[\sum _{i=1}^{n}(y_{i}-{\overline {y}})^{2}\right]\left[\sum _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}\right]}}=r_{y{\hat {y}}}^{2}$ .

Im Kontext der multiplen linearen Regression wird das Bestimmtheitsmaß auch als mehrfaches bzw. multiples Bestimmtheitsmaß bezeichnet. Aufgrund des oben aufgezeigten Zusammenhangs kann das multiple Bestimmtheitsmaß als eine Maßzahl für die Anpassungsgüte der geschätzten Regressionshyperebene ${\hat {y}}=b_{0}+x_{1}b_{1}+x_{2}b_{2}+\dotsc +x_{k}b_{k}$ an die Realisierungen $y_{1},y_{2},\ldots ,y_{n}$ der Zufallsvariablen $Y_{1},Y_{2},\ldots ,Y_{n}$ angesehen werden. Es ist also ein Maß des linearen Zusammenhangs zwischen $y_{i}$ und ${\hat {y}}_{i}$ .

Hierarchisch geordnete Modelle

Sei der $\mathbf x$ der Vektor der erklärenden Variablen. Ferner wird angenommen, dass $\mathbf x$ in zwei Teilvektoren ${\mathbf x}_{1}$ und $\mathbf {x} _{2}$ partitioniert wird, d.h. $\mathbf {x} =(\mathbf {x} _{1},\mathbf {x} _{2})$ . Sei weiterhin ${\mathtt {full}}$ das volle Modell $y_{i}=\beta _{0}+\mathbf {x} _{i1}^{\top }{\boldsymbol {\beta }}_{1}+\mathbf {x} _{i2}^{\top }{\boldsymbol {\beta }}_{2}+\varepsilon _{i}$ und ${\mathtt {sub}}$ und ein darin enthaltenes Teilmodell $y_{i}=\beta _{0}+\mathbf {x} _{i1}^{\top }{\boldsymbol {\beta }}_{1}+\varepsilon _{i}$ . Dann gilt ${\mathit {R}}_{\mathtt {full}}^{2}\geq {\mathit {R}}_{\mathtt {sub}}^{2}$ , d.h. für hierarchisch geordnete Modelle ist das Bestimmtheitsmaß des Teilmodells immer kleiner oder gleich dem Bestimmtheitsmaß des vollen Modells. Dies bedeutet, dass das Bestimmtheitsmaß mit zunehmender Anzahl der erklärenden Variablen automatisch ansteigt, ohne dass sich dabei die Güte der Anpassung signifikant verbessern muss.

Interpretation

Streudiagramm der Residuen ohne Struktur, das ${\mathit {R}}^{2}=0$ liefert

Streudiagramm der Residuen, das ein ${\mathit {R}}^{2}$ nahe bei liefert

Das Bestimmtheitsmaß lässt sich mit $100\,\%$ multiplizieren, um es in Prozent anzugeben: $100\,\%\cdot {\mathit {R}}^{2}$ ist dann der prozentuale Anteil der Streuung in , der durch das lineare Modell „erklärt“ wird, und liegt daher zwischen:

$0\,\%$ (oder $0$ ): kein linearer Zusammenhang und
$100\,\%$ (oder ): perfekter linearer Zusammenhang.

Je näher das Bestimmtheitsmaß am Wert Eins liegt, desto höher ist die „Bestimmtheit“ bzw. „Güte“ der Anpassung. Bei ${\mathit {R}}^{2}=0$ ist der lineare Schätzer ${\hat {y}}$ im Regressionsmodell völlig unbrauchbar für die Vorhersage des Zusammenhangs zwischen $x_{i}$ und $y_{i}$ (z.B. kann man das tatsächliche Gewicht der Person $y_{i}$ überhaupt nicht mit dem Schätzer ${\hat {y}}$ vorhersagen). Ist ${\mathit {R}}^{2}=1$ , dann lässt sich die abhängige Variable vollständig durch das lineare Regressionsmodell erklären. Anschaulich liegen dann die Messpunkte $(x_{1},y_{1}),(x_{2},y_{2}),\ldots ,(x_{n},y_{n})$ alle auf der (nichthorizontalen) Regressionsgeraden. Somit liegt bei diesem Fall kein stochastischer Zusammenhang vor, sondern ein deterministischer.

Durch die Aufnahme zusätzlicher erklärender Variablen kann das Bestimmtheitsmaß nicht sinken. Das Bestimmtheitsmaß hat die Eigenschaft, dass es i.d.R. durch die Hinzunahme weiterer erklärender Variablen steigt ( $k\uparrow \;\Rightarrow \;{\mathit {R}}^{2}\uparrow$ ), was scheinbar die Modellgüte steigert und zum Problem der Überanpassung führen kann. Das Bestimmtheitsmaß steigt durch die Hinzunahme weiterer erklärender Variablen, da durch die Hinzunahme dieser der Wert der Residuenquadratsumme sinkt. Auch wenn dem Modell irrelevante „erklärende Variablen“ hinzugefügt werden, können diese zu Erklärung der Gesamtstreuung beitragen und den R-Quadrat-Wert künstlich steigern. Da die Hinzunahme jeder weiteren erklärenden Variablen mit einem Verlust eines Freiheitsgrads verbunden ist, führt dies zu einer ungenaueren Schätzung. Wenn man Modelle mit einer unterschiedlichen Anzahl erklärender Variablen und gleichen unabhängigen Variablen vergleichen will, ist die Aussagekraft des Bestimmtheitsmaßes begrenzt. Um solche Modelle vergleichen zu können, wird ein „adjustiertes“ Bestimmtheitsmaß verwendet, welches zusätzlich die Freiheitsgrade berücksichtigt (siehe auch Abschnitt Das adjustierte Bestimmtheitsmaß).

Aus dem Bestimmtheitsmaß kann man im Allgemeinen nicht schließen, ob das angenommene Regressionsmodell dem tatsächlichen funktionalen Zusammenhang in den Messpunkten entspricht (siehe auch Abschnitt zu Grenzen und Kritik). Der Vergleich des Bestimmtheitsmaßes über Modelle hinweg ist nur sinnvoll, wenn eine gemeinsame abhängige Variable vorliegt und wenn die Modelle die gleiche Anzahl von Regressionsparametern und ein Absolutglied aufweisen. Da mit dem Bestimmtheitsmaß auch indirekt der Zusammenhang zwischen der abhängigen und den unabhängigen Variablen gemessen wird, ist es ein proportionales Fehlerreduktionsmaß.

In den Sozialwissenschaften sind niedrige R-Quadrat-Werte in Regressionsgleichungen nicht ungewöhnlich. Bei Querschnittsanalysen treten häufig niedrige R-Quadrat-Werte auf. Dennoch bedeutet ein kleines Bestimmtheitsmaß nicht notwendigerweise, dass die Kleinste-Quadrate-Regressionsgleichung unnütz ist. Es ist immer noch möglich, dass die Regressionsgleichung ein guter Schätzer für den ceteris paribus-Zusammenhang zwischen und ist. Ob die Regressionsgleichung ein guter Schätzer für den Zusammenhang von und ist hängt nicht direkt von der Größe des Bestimmtheitsmaßes ab.

Cohen und Cohen (1975) und Kennedy (1981) konnten zeigen, dass sich das Bestimmtheitsmaß graphisch mittels Venn-Diagrammen veranschaulichen lässt.

Konstruktion

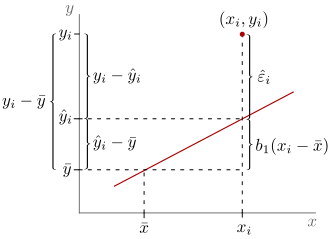
→ Hauptartikel: Totale Quadratsumme#Zerlegung der totalen Quadratsumme

Diese Graphik zeigt die Zerlegung der „zu erklärenden Abweichung“ bzw. „totalen Abweichung“ $\left(y_{i}-{\overline {y}}\right)$ in die „erklärte Abweichung“ $\left({\hat {y}}_{i}-{\overline {y}}\right)$ und die „nicht erklärte Abweichung“ bzw. „Restabweichung“ $\left(y_{i}-{\hat {y}}_{i}\right)$ .

Ausgangspunkt für die Konstruktion des Bestimmtheitsmaßes ist die Quadratsummenzerlegung, die als Streuungszerlegung interpretiert werden kann. In Bezug auf $\hat{y}_i$ lässt sich $y_{i}$ darstellen als

$y_{i}={\overline {y}}+\left({\hat {y}}_{i}-{\overline {y}}\right)+y_{i}-{\hat {y}}_{i}$

oder äquivalent

$\underbrace {(y_{i}-{\overline {y}})} _{\mathrm {zu\;erkl{\ddot {a}}rende\;Abweichung} }\quad =\quad \underbrace {({\hat {y}}_{i}-{\overline {y}})} _{\mathrm {erkl{\ddot {a}}rte\;Abweichung} }\quad +\quad \underbrace {(y_{i}-{\hat {y}}_{i})} _{\mathrm {nicht\;erkl{\ddot {a}}rte\;Abweichung} }$ ,

wobei $\left(y_{i}-{\overline {y}}\right)$ die Abweichung von $y_{i}$ vom Mittelwert $\overline y$ und $y_{i}-{\hat {y}}_{i}=\varepsilon _{i}$ die Restabweichung bzw. das Residuum darstellt. Die Gesamtabweichung lässt sich also zerlegen in die erklärte Abweichung und das Residuum. Die Gleichheit gilt auch dann noch, wenn man die Abweichungen quadriert (Abweichungsquadrate bildet) und anschließend über alle Beobachtungen summiert (Abweichungsquadratsummen, kurz: Quadratsummen bildet). Die totale Quadratsumme bzw. die zu „erklärende“ Quadratsumme lässt sich in die Quadratsumme der durch die Regressionsfunktion „erklärten“ Abweichungen vom Gesamtmittel (durch das Modell „erklärte“ Quadratsumme) und die Residuenquadratsumme (durch das Modell nicht „erklärte“ Quadratsumme) zerlegen. Die Quadratsummenzerlegung ergibt somit

$\underbrace {\sum \nolimits _{i=1}^{n}(y_{i}-{\overline {y}})^{2}} _{\mathrm {zu\;erkl{\ddot {a}}rende\;Quadratsumme} }\quad =\quad \underbrace {\sum \nolimits _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}} _{\mathrm {erkl{\ddot {a}}rte\;Quadratsumme} }\quad +\quad \underbrace {\sum \nolimits _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}} _{\mathrm {nicht\;erkl{\ddot {a}}rte\;Quadratsumme} }$ oder äquivalent dazu

$SQT=SQE+SQR$ .

Diese Zerlegung folgt in zwei Schritten. Im ersten Schritt wird eine Nullergänzung vorgenommen:

$\sum \nolimits _{i=1}^{n}(y_{i}-{\overline {y}})^{2}=\sum \nolimits _{i=1}^{n}(y_{i}-\underbrace {{\hat {y}}_{i}+{\hat {y}}_{i}} _{=0}-{\overline {y}})^{2}=\sum \nolimits _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}+2\underbrace {\sum \nolimits _{i=1}^{n}(y_{i}-{\hat {y}}_{i})({\hat {y}}_{i}-{\overline {y}})} _{=0}+\sum \nolimits _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}$ .

Diese Animation zeigt die Streuungszerlegung, d.h. die Zerlegung der Gesamtstreuung in die erklärte Streuung (der Anteil der Gesamtstreuung, der durch ${\hat {y}}$ erklärt werden kann) und die Reststreuung. Ebenfalls zu sehen ist, dass die – durch die Kleinste-Quadrate-Schätzung gewonnene – Regressionsgerade durch das „Gravitationszentrum“ $G({\overline {x}},{\overline {y}})$ der Punkteverteilung im Streudiagramm verläuft (siehe auch, algebraische Eigenschaften der Kleinste-Quadrate-Schätzer).

Im zweiten Schritt wurde die Eigenschaft benutzt, dass gewöhnliche Residuen ${\hat {\varepsilon }}_{i}=y_{i}-{\hat {y}}_{i}$ vorliegen, die mit den geschätzten Werten unkorreliert sind, d.h. $\textstyle \sum \nolimits _{i=1}^{n}{\hat {\varepsilon }}_{i}{\hat {y}}_{i}=0$ . Dies kann so interpretiert werden, dass in der Schätzung bereits alle relevante Information der erklärenden Variablen bezüglich der abhängigen Variablen steckt. Zudem wurde die Eigenschaft verwendet, dass – wenn das Modell das Absolutglied enthält – die Summe $\textstyle \sum \nolimits _{i=1}^{n}{\hat {\varepsilon }}_{i}=0$ und damit der empirische Mittelwert der Residuen Null ist. Dies folgt aus den verwendeten Schätzverfahren (Maximum-Likelihood-Schätzung bei der klassischen Normalregression oder Kleinste-Quadrate-Schätzung), denn dort müssen die ersten partiellen Ableitungen der Residuenquadratsumme nach $\beta_i$ gleich Null gesetzt werden um das Maximum bzw. Minimum zu finden, also für ${\hat {\beta }}_{0}$ : $\textstyle \sum \nolimits _{i=1}^{n}{\hat {\varepsilon }}_{i}=0$ bzw. für ${\hat {\beta }}_{k}$ mit $\textstyle \sum \nolimits _{i=1}^{n}x_{ij}{\hat {\varepsilon }}_{i}=0,\;j=1,2,\ldots ,k$ (siehe Algebraische Eigenschaften). Werden die Regressionsparameter mittels der Kleinste-Quadrate-Schätzung geschätzt, dann wird der Wert für ${\mathit {R}}^{2}$ automatisch maximiert, da die Kleinste-Quadrate-Schätzung die Residuenquadratsumme minimiert.

Im Anschluss an die Zerlegung dividiert man die Quadratsummenzerlegungsformel durch die totale Quadratsumme und erhält damit

$1={\frac {\sum \nolimits _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}}{\sum \nolimits _{i=1}^{n}(y_{i}-{\overline {y}})^{2}}}+{\frac {\sum \nolimits _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}}{\sum \nolimits _{i=1}^{n}(y_{i}-{\overline {y}})^{2}}}$

oder

${\frac {\sum \nolimits _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}}{\sum \nolimits _{i=1}^{n}(y_{i}-{\overline {y}})^{2}}}=1-{\frac {\sum \nolimits _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}}{\sum \nolimits _{i=1}^{n}(y_{i}-{\overline {y}})^{2}}}$ .

Das Verhältnis der durch die Regression erklärten Quadratsumme zur gesamten Quadratsumme

${\frac {\sum \nolimits _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}}{\sum \nolimits _{i=1}^{n}(y_{i}-{\overline {y}})^{2}}}={\mathit {R}}^{2}$

wird Bestimmtheitsmaß der Regression genannt. Aus der Quadratsummenzerlegungsformel wird ersichtlich, dass man das Bestimmtheitsmaß auch als

${\mathit {R}}^{2}={\frac {SQE}{SQT}}={\frac {SQT-SQR}{SQT}}=1-{\frac {SQR}{SQT}}$

darstellen kann. Wenn die obige Quadratsummenzerlegungsformel durch den Stichprobenumfang beziehungsweise durch die Anzahl der Freiheitsgrade (n-1) dividiert wird, erhält man die Varianzzerlegungsformel: $s_{y}^{2}=s_{\hat {y}}^{2}+s_{\hat {\varepsilon }}^{2}$ . Die Varianzzerlegung stellt eine additive Zerlegung der Varianz der abhängigen Variablen (totale Varianz bzw. Gesamtvarianz) s_y^2 in die Varianz der Schätzwerte $s_{\hat {y}}^{2}$ (erklärte Varianz) und die nicht erklärte Varianz $s_{\hat {\varepsilon }}^{2}$ (auch Residualvarianz genannt) dar. Hierbei entspricht die Residualvarianz dem Maximum-Likelihood-Schätzer ${\tilde {\sigma }}^{2}$ für die Varianz der Störgrößen $\sigma ^{2}$ . Aufgrund der Varianzzerlegung lässt sich das Bestimmtheitsmaß auch als ${\mathit {R}}^{2}=s_{\hat {y}}^{2}/s_{y}^{2}$ darstellen und wie folgt interpretieren: Das Bestimmtheitsmaß gibt an, wie viel Varianzaufklärung alle erklärenden Variablen $x_{1},x_{2},\ldots ,x_{n}$ an der Varianz der abhängigen Variablen s_y^2 leisten. Diese Interpretation ist jedoch nicht ganz korrekt, da die Quadratsummen eigentlich unterschiedliche Freiheitsgrade aufweisen. Diese Interpretation trifft eher auf das adjustierte Bestimmtheitsmaß zu, da hier die erwartungstreuen Varianzschätzer ins Verhältnis gesetzt werden. Im Gegensatz zur Varianzaufklärung beim Bestimmtheitsmaß kann man bei der Varianzaufklärung in der Hauptkomponenten- und Faktorenanalyse jeder Komponente bzw. jedem Faktor seinen Beitrag zur Aufklärung der gesamten Varianz zuordnen.

Einfache lineare Regression durch den Ursprung

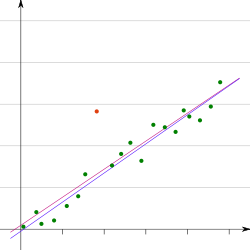
Die blaue Regressionsgerade verläuft durch den Ursprung und die violette nicht, da ein Ausreißer sie nach oben verschiebt.

Im Fall der einfachen linearen Regression durch den Ursprung/Regression ohne Absolutglied (das Absolutglied $\beta _{0}$ wird nicht in die Regression miteinbezogen und daher verläuft die Regressionsgleichung durch den Koordinatenursprung) lautet die konkrete empirische Regressionsgerade ${\tilde {y}}={\tilde {\beta }}_{1}x$ , wobei die Notation ${\tilde {y}},{\tilde {\beta }}_{1}$ benutzt wird um von der allgemeinen Problemstellung der Schätzung eines Steigungsparameters mit Hinzunahme eines Absolutglieds zu unterscheiden. Auch in einer einfachen linearen Regression durch den Ursprung lässt sich die Kleinste-Quadrate-Schätzung anwenden. Sie liefert für die Steigung $\textstyle {\tilde {\beta }}_{1}=\left(\textstyle \sum \nolimits _{i=1}^{n}x_{i}y_{i}\right)/\left(\textstyle \sum \nolimits _{i=1}^{n}x_{i}^{2}\right)$ . Dieser Schätzer für den Steigungsparameter ${\tilde {\beta }}_{1}$ entspricht dem Schätzer für den Steigungsparameter $b_{1}$ , dann und nur dann wenn ${\overline {x}}=0$ . Wenn für das wahre Absolutglied $\beta _{0}\neq 0$ gilt, ist ${\tilde {\beta }}_{1}$ ein verzerrter Schätzer für den wahren Steigungsparameter $\beta _{1}$ .

Wenn in eine Regressionsgleichung kein Absolutglied hinzugenommen wird, nimmt der aus der obigen Quadratsummenzerlegungsformel entnommene Ausdruck $\textstyle \sum \nolimits _{i=1}^{n}(y_{i}-{\hat {y_{i}}})({\hat {y}}_{i}-{\overline {y}})$ nicht den Wert Null an. Daher ist die oben angegebene Quadratsummenzerlegungsformel in diesem Fall nicht gültig. Wenn das Modell der Regression durch den Ursprung eine hinreichend schlechte Anpassung an die Daten liefert (d.h. die Daten variieren mehr um die Regressionslinie als um ${\overline {y}}$ ), was in $SQR>SQT$ resultiert und man die allgemeine Definition des Bestimmtheitsmaßes $1-SQR/SQT$ anwendet, dann führt dies zu einem negativen Bestimmtheitsmaß. Nach dieser Definition kann

${\mathit {R}}^{2}=1-{\frac {SQR}{SQT}}=1-{\frac {\displaystyle \sum \nolimits \left(y_{i}-{\tilde {\beta }}_{1}x_{i}\right)^{2}}{\displaystyle \sum \nolimits (y_{i}-{\overline {y}})^{2}}}$

also negativ werden. Ein negatives Bestimmtheitsmaß bedeutet dann, dass das empirische Mittel der abhängigen Variablen $\overline y$ eine bessere Anpassung an die Daten liefert als wenn man die erklärenden Variablen $x_{i}$ zur Schätzung benutzen würde. Um ein negatives Bestimmtheitsmaß zu vermeiden wird eine modifizierte Form der Quadratsummenzerlegung angegeben:

$\underbrace {\sum \nolimits _{i=1}^{n}y_{i}^{2}} _{\text{nicht korrigierte totale Quadratsumme}}=\underbrace {\sum \nolimits _{i=1}^{n}{\tilde {y}}_{i}^{2}} _{\mathrm {nicht\;korrigierte\;erkl{\ddot {a}}rte\;Quadratsumme} }+\underbrace {\sum \nolimits _{i=1}^{n}\left(y_{i}-{\tilde {y}}_{i}\right)^{2}} _{\text{Residuenquadratsumme}}$ oder äquivalent dazu

$SQT_{0}=SQE_{0}+SQR$ .

Diese modifizierte Form der Quadratsummenzerlegung wird auch nicht korrigierte Quadratsummenzerlegung genannt, da die erklärte und die totale Quadratsumme nicht um den empirischen Mittelwert „korrigiert“ bzw. „zentriert“ werden. Wenn man statt dem gewöhnlichen $SQT$ und $SQE$ die modifizierten Quadratsummen $SQT_{0}=\textstyle \sum \nolimits _{i=1}^{n}y_{i}^{2}$ und $SQE_{0}=\textstyle \sum \nolimits _{i=1}^{n}{\tilde {y}}_{i}^{2}$ benutzt, ist das Bestimmtheitsmaß gegeben durch

${\mathit {R}}^{2}\equiv {\frac {SQE_{0}}{SQT_{0}}}={\frac {\displaystyle \sum \nolimits {\tilde {y}}_{i}^{2}}{\displaystyle \sum \nolimits y_{i}^{2}}}=1-{\frac {SQR}{SQT_{0}}}=1-{\frac {\displaystyle \sum \nolimits \left(y_{i}-{\tilde {\beta }}_{1}x_{i}\right)^{2}}{\displaystyle \sum \nolimits y_{i}^{2}}}$ .

Dieses Bestimmtheitsmaß ist strikt nichtnegativ und wird – da es auf der nicht korrigierten Quadratsummenzerlegung aufbaut, bei der nicht um den empirischen Mittelwert „zentriert“ wird – auch als unzentriertes Bestimmtheitsmaß bezeichnet. Zur Abgrenzung wird das konventionelle Bestimmtheitsmaß auch als zentriertes Bestimmtheitsmaß bezeichnet. Bei einer Regression durch den Ursprung wird daher die modifizierte Form der Quadratsummenzerlegungsformel verwendet.

Rechenbeispiel

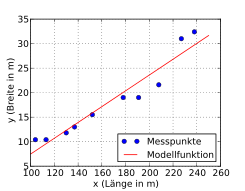
Streudiagramm der Längen und Breiten zehn zufällig ausgewählter Kriegsschiffe.

Folgendes Beispiel soll die Berechnung des Bestimmtheitsmaßes zeigen. Es wurden zufällig zehn Kriegsschiffe ausgewählt und bezüglich ihrer Länge und Breite (in Metern) analysiert. Es soll untersucht werden, ob die Breite eines Kriegsschiffs möglicherweise in einem festen Bezug zur Länge steht.

Das Streudiagramm lässt einen linearen Zusammenhang zwischen Länge und Breite eines Schiffs vermuten. Eine mittels der Kleinste-Quadrate-Schätzung durchgeführte einfache lineare Regression ergibt für das Absolutglied $b_{0}=-8{,}6450715$ und die Steigung $b_{1}=0{,}1612340$ (für die Berechnung der Regressionsparameter siehe Beispiel mit einer Ausgleichsgeraden). Die geschätzte Regressionsgerade lautet somit

${\widehat {\mathtt {breite}}}=-8{,}6450715+0{,}1612340\cdot {\mathtt {l{\ddot {a}}nge}}$ .

Die Gleichung stellt die geschätzte Breite ${\hat {y}}={\widehat {\mathtt {breite}}}$ als Funktion der Länge $x={\mathtt {l{\ddot {a}}nge}}$ dar. Die Funktion zeigt, dass die Breite der ausgewählten Kriegsschiffe grob einem Sechstel ihrer Länge entspricht.

Kriegsschiff	Länge (m)	Breite (m)	$y_{i}^{*}$	$y_{i}^{}\cdot y_{i}^{}$	${\hat {y}}_{i}$	${\hat {\varepsilon }}_{i}$	${\hat {\varepsilon }}_{i}^{2}$
	$x_{i}$	$y_{i}$	$y_{i}-{\overline {y}}$	$(y_{i}-{\overline {y}})^{2}$	${\hat {y}}(x_{i})$	$y_{i}-{\hat {y}}_{i}$	$(y_{i}-{\hat {y}}_{i})^{2}$
1	208	21,6	3,19	10,1761	24,8916	−3,2916	10,8347
2	152	15,5	−2,91	8,4681	15,8625	−0,3625	0,1314
3	113	10,4	−8,01	64,1601	9,5744	0,8256	0,6817
4	227	31,0	12,59	158,5081	27,9550	3,045	9,2720
5	137	13,0	−5,41	29,2681	13,4440	−0,4440	0,1971
6	238	32,4	13,99	195,7201	29,7286	2,6714	7,1362
7	178	19,0	0,59	0,3481	20,0546	−1,0546	1,1122
8	104	10,4	−8,01	64,1601	8,1233	2,2767	5,1835
9	191	19,0	0,59	0,3481	22,1506	−3,1506	9,9265
10	130	11,8	−6,61	43,6921	12,3154	−0,5154	0,2656
Σ	1678	184,1		574,8490		0,0000	44,7405
Σ/n	167,8	18,41		57,48490		0,0000	4,47405

Aus der Tabelle lässt sich erkennen, dass der Gesamtmittelwert der Breite ${\overline {y}}=18{,}41\;{\text{m}}$ beträgt, die totale Quadratsumme der Messwerte $574{,}849\;{\text{m}}^{2}$ beträgt und die Residuenquadratsumme $44{,}7405\;{\text{m}}^{2}$ beträgt. Daher ergibt sich das Bestimmtheitsmaß zu

${\mathit {R}}^{2}=1-{\frac {\displaystyle \sum \nolimits _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}}{\displaystyle \sum \nolimits _{i=1}^{n}(y_{i}-{\overline {y}})^{2}}}=1-{\frac {44{,}7405}{574{,}8490}}\;=\;0{,}92217$ ,

d.h. circa $92\,\%$ der Streuung in der Kriegsschiffsbreite kann durch die lineare Regression von Kriegsschiffsbreite auf Kriegsschiffslänge „erklärt“ werden. Das Komplement des Bestimmtheitsmaßes $1-{\mathit {R}}^{2}={\mathit {U}}^{2}$ wird auch Unbestimmtheitsmaß (auch Koeffizient der Nichtdetermination oder Alienationskoeffizient, von lateinisch alienus „fremd“, „unbekannt“) genannt. Bestimmtheits- und Unbestimmtheitsmaß addieren sich jeweils zu . Das Unbestimmtheitsmaß ${\mathit {U}}^{2}$ sagt im vorliegenden Beispiel aus, dass knapp $(1-{\mathit {R}}^{2})\cdot 100\,\%\approx 8\,\%$ der Streuung in der Breite „unerklärt“ bleiben. Hier könnte man z.B. nach weiteren Faktoren suchen, welche die Breite eines Kriegsschiffes beeinflussen und sie in die Regressionsgleichung mit aufnehmen.

Vergleich mit dem Standardfehler der Regression

Die „Qualität“ der Regression kann auch mithilfe des geschätzten Standardfehlers der Residuen (engl. residual standard error) beurteilt werden, der zum Standardoutput der meisten statistischen Programmpakete gehört. Der geschätzte Standardfehler der Residuen gibt an, mit welcher Sicherheit die Residuen ${\hat {\varepsilon }}_{i}$ den wahren Störgrößen $\varepsilon_i$ näherkommen. Die Residuen sind somit eine Approximation der Störgrößen. Der geschätzte Standardfehler der Residuen ist mit dem Bestimmtheitsmaß und dem adjustierten Bestimmtheitsmaß vergleichbar und ähnlich zu interpretieren. Der geschätzte Standardfehler der Residuen, der sich aus der obigen Tabelle berechnen lässt, ergibt einen Wert von:

${\tilde {s}}={\sqrt {{\tfrac {1}{n}}\sum \nolimits _{i=1}^{n}{\hat {\varepsilon }}_{i}^{2}}}={\sqrt {SQR/n}}=2{,}1152$ .

Es ist jedoch zu beachten, dass ${\tilde {s}}^{2}$ eine verzerrte Schätzung der wahren Varianz der Störgrößen $\sigma _{\varepsilon }^{2}=\sigma ^{2}$ ist, da der verwendete Varianzschätzer nicht erwartungstreu ist. Wenn man berücksichtigt, dass man durch die Schätzung der beiden Regressionsparameter $\beta _{0}$ und $\beta _{1}$ zwei Freiheitsgrade verliert und somit statt durch den Stichprobenumfang durch die Anzahl der Freiheitsgrade (n-2) dividiert, erhält man das „mittlere Residuenquadrat“ $MQR=SQR/(n-2)$ und damit die erwartungstreue Darstellung:

${\hat {\sigma }}={\sqrt {{\tfrac {1}{n-2}}\sum \nolimits _{i=1}^{n}{\hat {\varepsilon }}_{i}^{2}}}={\sqrt {MQR}}=2{,}3649$ .

Die Darstellung ist unverzerrt, da sie durch Einbezug der Freiheitsgrade der Varianzschätzer, wegen $\mathbb {E} ({\hat {\sigma }}^{2})=\sigma ^{2}$ , unter den Gauß-Markow-Annahmen erwartungstreu ist (siehe auch Schätzer für die Varianz der Störgrößen). Die unverzerrte Darstellung ${\hat {\sigma }}$ wird im Regressionsoutput statistischer Software oft auch als Standardfehler der Schätzung oder Standardfehler der Regression (engl. standard error of the regression, kurz: SER) bezeichnet.^{[A
7]} Der Standardfehler der Regression wird als Quadratwurzel des mittleren Residuenquadrats berechnet und ist ein eigenständiges Modellgütemaß. Er gibt an, wie groß im Durchschnitt die Abweichung der Messwerte von der Regressionsgerade ausfällt. Je größer der Standardfehler der Regression, desto schlechter beschreibt die Regressionsgerade die Verteilung der Messwerte. Der Standardfehler der Regression ist in der Regel kleiner als der Standardfehler der Zielgröße ${\hat {\sigma }}_{y}$ . Das Bestimmtheitsmaß wird häufiger angegeben als der Standardfehler der Residuen, obwohl der Standardfehler der Residuen bei der Bewertung Anpassungsgüte möglicherweise aussagekräftiger ist.

Missverständnisse, Grenzen und Kritik

Missverständnisse

Neben den Vorteilen des Bestimmtheitsmaßes (es ist eine dimensionslose Größe, hat eine einfache Interpretation und liegt stets zwischen $0$ und ) wird das Bestimmtheitsmaß immer wieder kritisiert und falsch angewendet:

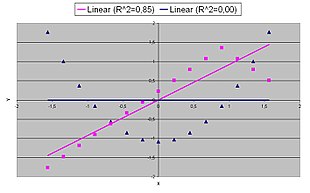
Beispiele für Daten mit einem hohen (pink) und einem niedrigen (blau) Bestimmtheitsmaß bei einem zugrunde gelegten linearen Modell

Übliche Missverständnisse sind:
- Bei einem hohen Bestimmtheitsmaß für einen Schätzer könne man folgern, dass der tatsächliche Zusammenhang linear sei. Die pinken Daten in der Grafik wurden mit einer nichtlinearen Funktion generiert:^{[A
  8]}

$f(x)\equiv -{\tfrac {4}{3}}\left|x-0{,}9\right|+1{,}4$

Durch die Betragsfunktion im Term nimmt die Funktion an der Stelle 0{,}9 ihr Maximum $1{,}49$ an. Für höhere Werte von $x>0{,}9$ fällt die Funktion dann streng monoton mit der Steigung $-4/3$ . Damit wäre der tatsächliche Zusammenhang in den Daten auch bei dem hohen Bestimmtheitsmaß nach Konstruktion natürlich nicht linear. Dennoch legt das hohe Bestimmtheitsmaß nahe, dass es sich um einen linearen Zusammenhang handelt.

Ein hohes Bestimmtheitsmaß gebe an, dass die geschätzte Regressionslinie überall eine gute Approximation an die Daten darstellt; die pinken Daten legen auch hier etwas anderes nahe.
Ein Bestimmtheitsmaß nahe bei Null zeige an, dass es keinen Zusammenhang zwischen der abhängigen und den unabhängigen Variablen gebe. Die blauen Daten in der Grafik wurden mit der folgenden quadratischen Funktion generiert und besitzen daher einen deterministischen funktionalen Zusammenhang, der allerdings nicht linear ist^{[A
9]}

$g(x)\equiv 1{,}1x^{2}-1{,}1$ .

Obwohl das Bestimmtheitsmaß gleich Null ist, lässt sich nicht daraus schließen, dass es keinen Zusammenhang zwischen der abhängigen und den unabhängigen Variablen für die konstruierten Datenpunkte gibt. Eine Regressionsanalyse für nichtlineare Fälle verallgemeinert die lineare Regression auf andere Klassen von Funktionen und mehrdimensionale Definitionsbereiche von .

Wählt man aus den Daten mit quadratischem Zusammenhang (Parabel ) nur die Datenpunkte mit positivem -Werten aus, kann auch das Bestimmtheitsmaß sehr hoch sein und bei einem nach Konstruktion der Daten gegebenen quadratischem Zusammenhang durch in den Messdaten dennoch eine lineare Modellannahme suggerieren (z.B. wenn man nur die Daten aus der Parabel wählt, in der die Funktion positive Steigung besitzt).

Grenzen und Kritik

Dieses Streudiagramm zeigt die Regressionsgrade einer linearen Einfachregression, die optimal durch die „Punktwolke“ der Messung gelegt wurde. An der waagerechten Achse ist das Wachstum des realen BIP und auf der senkrechten Achse ist die Veränderung der Arbeitslosenquote in den USA (1961–2007) abgetragen. Die starke Korrelation zwischen beiden Größen (genannt Okunsches Gesetz) kommt visuell dadurch zum Ausdruck, dass sich die Regressiongerade gut an die Datenpunkte anpasst. Formal lässt sie sich anhand eines relativ hohen R-Quadrat-Wertes erkennen (hier: ${\mathit {R}}^{2}=69{,}20\,\%$ ). Bei Betrachtung des Streudiagramms und des R-Quadrat-Wertes wird Kausalität suggeriert (starkes Wirtschaftswachstum ist die kausale Ursache für die Reduktion in der Arbeitslosigkeit). Das Bestimmtheitsmaß gibt allerdings nur Auskunft über die Stärke des Zusammenhangs, nicht über Kausalität.

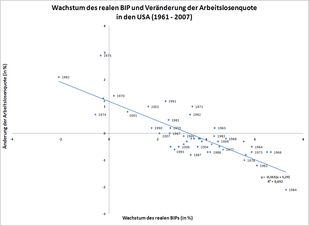
Das Bestimmtheitsmaß zeigt zwar die „Qualität“ der linearen Approximation, jedoch nicht, ob das Modell richtig spezifiziert wurde. Zum Beispiel kann ein nichtlinearer Zusammenhang bei einer der unabhängigen Variablen vorliegen. In einem solchen Fall können die unabhängigen Variablen unentdeckte Erklärungskraft enthalten, auch dann wenn das Bestimmtheitsmaß einen Wert nahe bei Null aufweist. Modelle, die mittels der Kleinste-Quadrate-Schätzung geschätzt wurden, werden daher die höchsten R-Quadrat-Werte aufweisen.
(Korrelation/Kausaler Zusammenhang) Das Bestimmtheitsmaß sagt nichts darüber aus, ob die unabhängige Variable der Grund (die kausale Ursache) für die Änderungen in sind. Zum Beispiel kann das Bestimmtheitsmaß zwischen der Anzahl der Störche $x_{i}$ und der Anzahl der neugeborenen Kinder $y_{i}$ in untersuchten Gebieten $G_{i}$ hoch sein. Ein direkter kausaler Zusammenhang zwischen Störchen und Neugeborenen ist jedoch biologisch ausgeschlossen.
Das Bestimmtheitsmaß sagt nichts über die statistische Signifikanz des ermittelten Zusammenhangs und der einzelnen erklärenden Variablen aus. Um diesen zu ermitteln muss die Stichprobengröße bekannt sein und ein Signifikanztest durchgeführt werden.
Das Bestimmtheitsmaß macht keine Aussage über Multikollinearität zwischen den unabhängigen Variablen $x_{i}$ . Multikollinearität kann z.B. mithilfe des Varianzinflationsfaktors identifiziert werden (siehe auch Abschnitt Interpretation der Varianz der Regressionsparameter).
Es zeigt nicht an, ob eine Verzerrung durch ausgelassene Variablen (engl. omitted variable bias) vorliegt.
Es macht keine Aussage, ob eine Transformation der Daten die Erklärungskraft der Regression verbessert.
Ein Nachteil des Bestimmtheitsmaßes ist die Empfindlichkeit gegenüber Trends: Wenn sich eine exogene Variable parallel zu einer erklärenden entwickelt, werden unabhängig von der wahren Erklärungskraft des Modells hohe R-Quadrat-Werte ausgewiesen.
Zusammenfassend ist ein hohes Bestimmtheitsmaß kein Beweis für ein „gutes“ Modell und ein niedriges Bestimmtheitsmaß bedeutet nicht, dass es sich um ein „schlechtes“ Modell handelt. Dies wird anhand des Anscombe-Beispiels (1973) deutlich. Anscombe zeigte auf der Basis von vier verschiedenen Datensätzen, dass ein in allen vier Fällen relativ hohes Bestimmtheitsmaß von $0{,}67$ nichts darüber aussagt, ob der wahre Zusammenhang zwischen zwei Variablen richtig erfasst worden ist.

Geschichte

Francis Galton

Karl Pearson

Die Grundlage des Bestimmtheitsmaßes stellt die Regressionsanalyse und der Korrelationskoeffizient dar. Der britische Naturforscher Sir Francis Galton (1822–1911) begründete in den 1870er-Jahren die Regressionsanalyse. Er war – wie auch sein Cousin Charles Darwin – ein Enkel von Erasmus Darwin. Galton war durch seine starke Leidenschaft Daten jeglicher Art zu sammeln bekannt. Beispielsweise sammelte er Daten der Samen von Platterbsen. Beim Vergleich der Durchmesser der Samen konstruierte er das, was heute allgemein als Korrelationsdiagramm bekannt ist. Den bei dieser Tätigkeit von ihm entdeckte Zusammenhang taufte er zunächst „Reversion“ (Umkehrung); später entschied er sich jedoch für die Bezeichnung „Regression“. Bei der Analyse der Samen entdeckte er das Phänomen der Regression zur Mitte, nach dem – nach einem extrem ausgefallenen Messwert – die nachfolgende Messung wieder näher am Durchschnitt liegt: Der Mediandurchmesser der Nachkommen der größeren Samen war kleiner als der Mediandurchmesser der Samen der Eltern (vice versa). In seine Korrelationsdiagramme zeichnete er eine Trendlinie ein, für die er als Steigung den Korrelationskoeffizienten verwendete.

Die Bezeichnung „Varianz“ wurde vom Statistiker Ronald Fisher (1890–1962) in seinem 1918 veröffentlichtem Aufsatz mit dem Titel Die Korrelation zwischen Verwandten in der Annahme der Mendelschen Vererbung (Originaltitel: The Correlation between Relatives on the Supposition of Mendelian Inheritance) eingeführt. Fisher war einer der bedeutendsten Statistiker des 20. Jahrhunderts und ist für seine Beiträge zur Evolutionstheorie berühmt. Ebenso ist er für die Entdeckung der Streuungszerlegung (engl. analysis of variance) bekannt, die die Grundlage für das Bestimmtheitsmaß darstellt. Die – eng in Verbindung mit dem Bestimmtheitsmaß stehende – F -Statistik ist ebenfalls nach ihm benannt. Karl Pearson (1857–1936), der Begründer der Biometrie, lieferte schließlich eine formal-mathematische Begründung für den Korrelationskoeffizienten, dessen Quadrat dem Bestimmtheitsmaß entspricht.

Das Bestimmtheitsmaß wurde in den folgenden Jahren stark kritisiert. Dies geschah auch da es die Eigenschaft hat, dass es umso größer wird, je größer die Zahl der unabhängigen Variablen ist. Dies ist unabhängig davon, ob die zusätzlichen erklärenden Variablen einen Beitrag zur Erklärungskraft liefern. Um diesen Umstand Rechnung zu tragen, schlug der Ökonometriker Henri Theil 1961 das adjustierte Bestimmtheitsmaß (auch bereinigtes, korrigiertes oder angepasstes Bestimmtheitsmaß genannt) vor. Dies berücksichtigt, dass die Hinzunahme jeder weiteren erklärenden Variablen mit einem Verlust eines Freiheitsgrads verbunden ist, wurde jedoch von Rinne (2004) in der Hinsicht kritisiert, dass das Auswahlkriterium den Verlust an Freiheitsgraden mit wachsender Anzahl an erklärenden Variablen nicht ausreichend bestraft.

Das adjustierte Bestimmtheitsmaß

Definition

Das Bestimmtheitsmaß ${\mathit {R}}^{2}$ hat die Eigenschaft, dass es umso größer wird, je größer die Zahl der unabhängigen Variablen ist. Dies ist unabhängig davon, ob die zusätzlichen unabhängigen Variablen einen Beitrag zur Erklärungskraft liefern. Daher ist es ratsam, das adjustierte (freiheitsgradbezogene) Bestimmtheitsmaß (auch bereinigtes, korrigiertes oder angepasstes Bestimmtheitsmaß genannt) zu Rate zu ziehen. Das adjustierte Bestimmtheitsmaß nach Theil wird mit ${\overline {\mathit {R}}}{}^{2}$ (lies: R Quer Quadrat) oder ${\mathit {R}}_{\text{adj.}}^{2}$ bzw. ${\mathit {R}}_{a}^{2}$ notiert. Man erhält das adjustierte Bestimmtheitsmaß, wenn an Stelle der Quadratsummen die mittleren Abweichungsquadrate (englisch mean squares) $MQR=SQR/(n-p)$ und $MQT=SQT/(n-1)$ verwendet werden:

${\overline {\mathit {R}}}{}^{2}\equiv 1-{\frac {MQR}{MQT}}=1-{\frac {SQR}{SQT}}{\frac {n-1}{n-p}}=1-\left(1-{\mathit {R}}^{2}\right){\frac {n-1}{n-p}}$ .

Hierbei ist $MQR$ das „mittlere Residuenquadrat“ (Mittleres Quadrat der Residuen, kurz: MQR) und $MQT$ das „mittlere Gesamtabweichungsquadrat“ (Mittleres Quadrat der Totalen Abweichungen, kurz: MQT). Das adjustierte Bestimmtheitsmaß modifiziert die Definition des Bestimmtheitsmaßes, indem es den Quotienten $SQR/SQT$ mit dem Faktor $(n-1)/(n-p)$ multipliziert. Alternativ lässt sich das adjustierte Bestimmtheitsmaß algebraisch äquivalent darstellen als

${\overline {\mathit {R}}}{}^{2}={\mathit {R}}^{2}-\left(1-{\mathit {R}}^{2}\right){\frac {k}{n-p}}$ .

Definitionsgemäß ist das adjustierte Bestimmtheitsmaß für mehr als eine erklärende Variable stets kleiner als das unadjustierte. Beim adjustierten Bestimmtheitsmaß wird die Erklärungskraft des Modells, repräsentiert durch ${\mathit {R}}^{2}$ , ausbalanciert mit der Komplexität des Modells, repräsentiert durch $p=k+1$ , die Anzahl der Parameter. Je komplexer das Modell ist, desto mehr „bestraft“ das adjustierte Bestimmtheitsmaß jede neu hinzugenommene erklärende Variable. Das adjustierte Bestimmtheitsmaß steigt nur, wenn ${\mathit {R}}^{2}$ ausreichend steigt, um den gegenläufigen Effekt des Quotienten $(n-1)/(n-p)$ auszugleichen und kann ebenfalls sinken ( $k\uparrow \;\Rightarrow \;{\overline {\mathit {R}}}{}^{2}\uparrow \downarrow$ ). Auf diese Weise lässt sich ${\overline {R}}{}^{2}$ als Entscheidungskriterium bei der Auswahl zwischen zwei alternativen Modellspezifikationen (etwa einem restringierten und einem unrestringierten Modell) verwenden. Das adjustierte Bestimmtheitsmaß kann negative Werte annehmen und ist kleiner als das unbereinigte, außer falls ${\mathit {R}}^{2}=1$ und damit auch ${\overline {\mathit {R}}}{}^{2}=1$ ist. Als Ergebnis daraus folgt ${\overline {\mathit {R}}}{}^{2}\leq {\mathit {R}}^{2}$ . Das adjustierte Bestimmtheitsmaß nähert sich mit steigendem Stichprobenumfang dem unadjustierten Bestimmtheitsmaß. Dies liegt daran, dass bei fixer Anzahl der erklärenden Variablen für den Grenzwert für den Korrekturfaktor bzw. Strafterm gilt

$\lim _{n\to \infty }{\frac {n-1}{n-p}}=\lim _{n\to \infty }{\frac {1-{\frac {1}{n}}}{1-{\frac {p}{n}}}}=1$ .

In der Praxis ist es nicht zu empfehlen das adjustierte Bestimmtheitsmaß zu verwenden, da die „Bestrafung“ für neu hinzugefügte erklärende Variablen zu klein erscheint. Man kann zeigen, dass das ${\overline {\mathit {R}}}{}^{2}$ schon steigt, wenn eine erklärende Variable mit einem t-Wert größer als Eins in das Modell inkludiert wird. Aus diesem Grund wurden weitere Kriterien (sogenannte Informationskriterien) wie z.B. das Akaike-Informationskriterium und das bayessche Informationskriterium zur Modellauswahl entwickelt, die ebenfalls der Idee von Ockhams Rasiermesser folgen, dass ein Modell nicht unnötig komplex sein soll.

Konstruktion

Aus der allgemeinen Definition von ${\mathit {R}}^{2}$ folgt, dass

${\mathit {R}}^{2}=1-{\frac {\displaystyle {\frac {1}{n}}\sum \nolimits \nolimits _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}}{\displaystyle {\frac {1}{n}}\sum \nolimits \nolimits _{i=1}^{n}(y_{i}-{\overline {y}})^{2}}}=1-{\frac {{\tilde {s}}_{\hat {\varepsilon }}^{2}}{{\tilde {s}}_{y}^{2}}}$ .

Wir wissen jedoch, dass ${\tilde {s}}_{\hat {\varepsilon }}^{2}$ und ${\tilde {s}}_{y}^{2}$ verzerrte Schätzer für die wahre Varianz der Störgrößen $\sigma ^{2}$ und die der Messwerte $\sigma _{y}^{2}$ sind. Aus dieser Tatsache wird deutlich, dass es sich beim multiplen Bestimmtheitsmaß ${\mathit {R}}^{2}$ um eine Zufallsvariable handelt: Das multiple Bestimmtheitsmaß kann man als Schätzfunktion für das unbekannte Bestimmtheitsmaß in der Grundgesamtheit $\rho ^{2}$ ^{[A
10]} (lies: rho Quadrat) betrachten. Dieses ist gegeben durch

$\rho ^{2}=1-{\frac {\sigma ^{2}}{\sigma _{y}^{2}}}$

und ist der Anteil der Streuung in in der Grundgesamtheit, der durch die erklärenden Variablen „erklärt“ wird. Dividiert man die jeweiligen Quadratsummen durch ihre Freiheitsgrade, so erhält man jeweils das durchschnittliche Abweichungsquadrat (Varianz):

${\hat {\sigma }}^{2}={\frac {1}{n-p}}\sum \nolimits \nolimits _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}\quad$ und $\quad {\hat {\sigma }}_{y}^{2}={\frac {1}{n-1}}\sum \nolimits \nolimits _{i=1}^{n}(y_{i}-{\overline {y}})^{2}$ .

Die Varianzen ${\hat {\sigma }}^{2}$ und ${\hat {\sigma }}_{y}^{2}$ sind erwartungstreue Schätzer für die wahre Varianz der Störgrößen $\sigma ^{2}$ und die der Messwerte $\sigma _{y}^{2}$ . Setzt man nun bei ${\mathit {R}}^{2}$ oben und unten die unverzerrten Schätzer ein, so erhält man das adjustierte Bestimmtheitsmaß:

${\overline {\mathit {R}}}{}^{2}=1-{\frac {\displaystyle {\frac {1}{n-p}}\sum \nolimits \nolimits _{i=1}^{n}(y_{i}-{\hat {y}}_{i})^{2}}{\displaystyle {\frac {1}{n-1}}\sum \nolimits \nolimits _{i=1}^{n}(y_{i}-{\overline {y}})^{2}}}=1-{\frac {{\hat {\sigma }}^{2}}{SQT/(n-1)}}$ .

Durch algebraische Umformungen erhält man schließlich

${\overline {\mathit {R}}}{}^{2}=1-\left(1-{\mathit {R}}^{2}\right){\frac {n-1}{n-p}}$ .

Das adjustierte Bestimmtheitsmaß ${\overline {\mathit {R}}}{}^{2}$ entspricht also dem um die unverzerrten Komponenten adjustiertem Bestimmtheitsmaß ${\mathit {R}}^{2}$ . Oft wird das adjustierte Bestimmtheitsmaß auch korrigiertes Bestimmtheitsmaß genannt. Dies ist keine gute Bezeichnung, da sie impliziert dass ${\overline {\mathit {R}}}{}^{2}$ in einer Weise „besser“ ist als ${\mathit {R}}^{2}$ , um das Bestimmtheitsmaß in der Grundgesamtheit $\rho ^{2}$ zu schätzen. Dies ist aber nicht der Fall, da das Verhältnis zweier unverzerrter Schätzer kein unverzerrter Schätzer ist. Auch die Bezeichnung „adjustiertes R-Quadrat“ kann irreführend sein, da ${\overline {\mathit {R}}}{}^{2}$ wie in obiger Formel nicht als das Quadrat irgendeiner Quantität berechnet wird.

Matrixschreibweise

Das Bestimmtheitsmaß

In der multiplen linearen Regression, mit dem multiplen linearen Modell in Matrixschreibweise

${\begin{pmatrix}y_{1}\\y_{2}\\\vdots \\y_{n}\end{pmatrix}}_{(n\times 1)}\quad =\quad {\begin{pmatrix}1&x_{11}&x_{12}&\cdots &x_{1k}\\1&x_{21}&x_{22}&\cdots &x_{2k}\\\vdots &\vdots &\vdots &\ddots &\vdots \\1&x_{n1}&x_{n2}&\cdots &x_{nk}\end{pmatrix}}_{(n\times p)}\quad \cdot \quad {\begin{pmatrix}\beta _{0}\\\beta _{1}\\\vdots \\\beta _{k}\end{pmatrix}}_{(p\times 1)}\quad +\quad {\begin{pmatrix}\varepsilon _{1}\\\varepsilon _{2}\\\vdots \\\varepsilon _{n}\end{pmatrix}}_{(n\times 1)}$ beziehungsweise in Kurzform $\;\mathbf {y} =\mathbf {X} {\boldsymbol {\beta }}+{\boldsymbol {\varepsilon }}$ ,

ergibt sich das Bestimmtheitsmaß durch die korrigierte Quadratsummenzerlegung (um den Mittelwert bereinigte Quadratsummenzerlegung)

$\underbrace {\left(\mathbf {y} -{\overline {\mathbf {y} }}\right)^{\top }\left(\mathbf {y} -{\overline {\mathbf {y} }}\right)} _{\mathrm {zuerkl{\ddot {a}}rende\;Quadratsumme} }\quad =\quad \underbrace {\left({\hat {\mathbf {y} }}-{\overline {\mathbf {y} }}\right)^{\top }\left({\hat {\mathbf {y} }}-{\overline {\mathbf {y} }}\right)} _{\mathrm {erkl{\ddot {a}}rte\;Quadratsumme} }\quad +\quad \underbrace {\left(\mathbf {y} -{\hat {\mathbf {y} }}\right)^{\top }\left(\mathbf {y} -{\hat {\mathbf {y} }}\right)} _{\mathrm {nicht\;erkl{\ddot {a}}rte\;Quadratsumme} }$ .

Die Bezeichnung „korrigiert“ hebt hervor, dass man die Summe über alle Beobachtungen der quadrierten Werte nimmt, nachdem um den Mittelwert „korrigiert“ wurde. Hierbei ist ${\overline {\mathbf {y} }}$ ein Vektor mit den Elementen $\overline y$ und ${\hat {\mathbf {y} }}$ ist definiert durch ${\hat {\mathbf {y} }}=\mathbf {X} \mathbf {b}$ , wobei $\mathbf {b} =\left(\mathbf {X} ^{\top }\mathbf {X} \right)^{-1}\mathbf {X} ^{\top }\mathbf {y}$ den -->Kleinste-Quadrate-Schätzvektor darstellt. Das Bestimmtheitsmaß ist dann gegeben durch:

${\mathit {R}}^{2}=1-{\frac {SQR}{SQT}}=1-{\frac {\left(\mathbf {y} -\mathbf {X} \mathbf {b} \right)^{\top }\left(\mathbf {y} -\mathbf {X} \mathbf {b} \right)}{\left(\mathbf {y} -{\overline {\mathbf {y} }}\right)^{\top }(\mathbf {y} -{\overline {\mathbf {y} }})}}=1-{\frac {{\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}}}{{\hat {\mathbf {y} }}^{\top }{\hat {\mathbf {y} }}+{\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}}-n{\overline {y}}^{2}}}$

Häufig findet sich auch die algebraisch äquivalente Darstellung

${\mathit {R}}^{2}=1-{\frac {\mathbf {y} ^{\top }\mathbf {y} -\mathbf {b} ^{\top }\mathbf {X} ^{\top }\mathbf {y} }{\mathbf {y} ^{\top }\mathbf {y} -n{\overline {y}}^{2}}}$ .

oder

${\mathit {R}}^{2}={\frac {SQE}{SQT}}={\frac {{\hat {\mathbf {y} }}^{\top }{\hat {\mathbf {y} }}-n{\overline {\hat {y}}}^{2}}{{\hat {\mathbf {y} }}^{\top }{\hat {\mathbf {y} }}+{\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}}-n{\overline {y}}^{2}}}={\frac {\mathbf {b} ^{\top }\mathbf {X} ^{\top }\mathbf {y} -n{\overline {y}}^{2}}{\mathbf {y} ^{\top }\mathbf {y} -n{\overline {y}}^{2}}}$ .

Die letzte Gleichheit ergibt sich aus dem Umstand, dass sich ${\hat {\mathbf {y} }}=\mathbf {X} \mathbf {b}$ aus der linksseitigen Multiplikation von $\mathbf{y}$ mit der Prädiktionsmatrix $\mathbf{P}$ ergibt. Die Berechnung des Bestimmtheitsmaßes lässt sich in folgender Tafel der Varianzanalyse zusammenfassen:

Variationsquelle	Abweichungsquadratsumme	Anzahl der Freiheitsgrade	Mittleres Abweichungsquadrat
Regression (erklärt)	$\mathbf {b} ^{\top }\mathbf {X} ^{\top }\mathbf {y} -n{\overline {y}}^{2}$
Residuen (unerklärt)	${\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}}$	$(n-p)$	${\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}}/(n-p)={\hat {\sigma }}^{2}$
Gesamt	$\mathbf {y} ^{\top }\mathbf {y} -n{\overline {y}}^{2}$		$SQT/(n-1)=s_{y}^{2}$
Bestimmtheitsmaß	$1-{\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}}/(\mathbf {y} ^{\top }\mathbf {y} -n{\overline {y}}^{2})={\mathit {R}}^{2}$

Falls das lineare Modell das Absolutglied enthält, dann entspricht der empirische Mittelwert der Schätzwerte dem der beobachteten Messwerte, wegen

${\overline {\hat {y}}}={\frac {\sum \nolimits _{i=1}^{n}{\hat {y_{i}}}}{n}}={\frac {\mathbf {x} _{(0)}^{\top }{\hat {\mathbf {y} }}}{n}}={\frac {\mathbf {x} _{(0)}^{\top }\mathbf {X} \mathbf {b} }{n}}={\frac {\mathbf {x} _{(0)}^{\top }\left(\mathbf {y} -{\hat {\boldsymbol {\varepsilon }}}\right)}{n}}={\frac {\mathbf {x} _{(0)}^{\top }\mathbf {y} }{n}}={\frac {\sum \nolimits _{i=1}^{n}y_{i}}{n}}={\overline {y}}$ ,

wobei $\mathbf {x} _{(0)}$ die, aus Einsen bestehende, erste Spalte der Datenmatrix $\mathbf {X}$ darstellt. Es wurde die Eigenschaft benutzt, dass der Vektor der KQ-Residuen und der Vektor der erklärenden Variablen orthogonal und damit unkorreliert sind, d.h es gilt $\mathbf {x} _{(0)}^{\top }{\hat {\boldsymbol {\varepsilon }}}=\mathbf {0}$ (siehe auch, algebraische Eigenschaften der Kleinste-Quadrate-Schätzer).

Darstellung mittels Projektionsmatrix

Die Quadratsummenzerlegung und das Bestimmtheitsmaß lassen sich ebenfalls mittels einer speziellen idempotenten und symmetrischen $(n \times n)$ -Projektionsmatrix $\mathbf {M} ^{0}=(\mathbf {I} -(\mathbf {1} \mathbf {1} ^{\top })/n)$ darstellen, die den Vektor $\mathbf {y} \in \mathbb {R} ^{n}$ mit den Elementen $y_{i}$ in den Vektor Abweichungen

$\mathbf {M} ^{0}\mathbf {y} ={\begin{pmatrix}(y_{1}-{\overline {y}})\\(y_{2}-{\overline {y}})\\\vdots \\(y_{n}-{\overline {y}})\\\end{pmatrix}}$

mit Elementen $(y_{i}-{\overline {y}})$ transformiert. Die linksseitige Multiplikation von $\mathbf{y}$ mit $\mathbf {M} ^{0}$ zentriert den Vektor $\mathbf{y}$ . Daher wird diese Matrix auch als zentrierende Matrix bezeichnet. Die totale Quadratsumme lässt sich also mittels der zentrierenden Matrix auch darstellen als $SQT=\mathbf {y} ^{\top }\mathbf {M} ^{0}\mathbf {y}$ . Analog dazu lässt sich die Quadratsumme der Schätzwerte $\hat{y}_i$ schreiben als $SQE={\hat {\mathbf {y} }}^{\top }\mathbf {M} ^{0}{\hat {\mathbf {y} }}=\mathbf {b} ^{\top }\mathbf {X} ^{\top }\mathbf {M} ^{0}\mathbf {X} \mathbf {b}$ und die Residuenquadratsumme als $SQR={\hat {\boldsymbol {\varepsilon }}}^{\top }\mathbf {M} ^{0}{\hat {\boldsymbol {\varepsilon }}}={\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}}$ . Dadurch erhält man die Quadratsummenzerlegung als

$\mathbf {y} ^{\top }\mathbf {M} ^{0}\mathbf {y} =\mathbf {b} ^{\top }\mathbf {X} ^{\top }\mathbf {M} ^{0}\mathbf {X} \mathbf {b} +{\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}}$

wobei sich zeigen lässt, dass für die Streuung der Messwerte und die der Schätzwerte folgender Zusammenhang gilt: ${\hat {\mathbf {y} }}^{\top }\mathbf {M} ^{0}{\hat {\mathbf {y} }}={\hat {\mathbf {y} }}^{\top }\mathbf {M} ^{0}\mathbf {y}$ . Mithilfe dieses Zusammenhangs kann man zeigen, dass das multiple Bestimmtheitsmaß dem Quadrat des Korrelationskoeffizienten zwischen $\mathbf y$ und ${\hat {\mathbf {y} }}$ entspricht:

Beweis

${\begin{aligned}{\mathit {R}}^{2}={\frac {{\hat {\mathbf {y} }}^{\top }\mathbf {M} ^{0}{\hat {\mathbf {y} }}}{\mathbf {y} ^{\top }\mathbf {M} ^{0}\mathbf {y} }}={\frac {\left({\hat {\mathbf {y} }}^{\top }\mathbf {M} ^{0}{\hat {\mathbf {y} }}\right)^{2}}{\left(\mathbf {y} ^{\top }\mathbf {M} ^{0}\mathbf {y} \right)\left({\hat {\mathbf {y} }}^{\top }\mathbf {M} ^{0}{\hat {\mathbf {y} }}\right)}}&={\frac {\left({\hat {\mathbf {y} }}^{\top }\mathbf {M} ^{0}\mathbf {y} \right)^{2}}{\left(\mathbf {y} ^{\top }\mathbf {M} ^{0}\mathbf {y} \right)\left({\hat {\mathbf {y} }}^{\top }\mathbf {M} ^{0}{\hat {\mathbf {y} }}\right)}}\\&={\frac {\left[\sum _{i=1}^{n}(y_{i}-{\overline {y}})({\hat {y}}_{i}-{\overline {y}})\right]^{2}}{\left[\sum _{i=1}^{n}(y_{i}-{\overline {y}})^{2}\right]\left[\sum _{i=1}^{n}({\hat {y}}_{i}-{\overline {y}})^{2}\right]}}=\left({\frac {SP_{y{\hat {y}}}}{\sqrt {SQ_{y}SQ_{\hat {y}}}}}\right)^{2}=r_{\mathbf {y} {\hat {\mathbf {y} }}}^{2}\end{aligned}}$

Die Notation $\mathbf {M} ^{0}$ für die Matrix $(\mathbf {I} -(\mathbf {1} \mathbf {1} ^{\top })/n)$ rührt daher, dass die residuenerzeugende Matrix $\mathbf {M} =\mathbf {I} -\mathbf {P}$ – wobei $\mathbf {P} =\mathbf {X} \left(\mathbf {X} ^{\top }\mathbf {X} \right)^{-1}\mathbf {X} ^{\top }$ die Prädiktionsmatrix darstellt – für den Fall, dass $\mathbf {X} =\mathbf {1}$ der Matrix $\mathbf {M} ^{0}$ entspricht. Die Matrix $\mathbf {M} ^{0}$ ist also ein Spezialfall der residuenerzeugenden Matrix.

Das adjustierte Bestimmtheitsmaß

Man kann zeigen, dass die Veränderung des Bestimmtheitsmaßes, wenn eine zusätzliche Variable der Regression hinzugefügt wird

${\mathit {R}}_{\mathbf {X} z}^{2}={\mathit {R}}_{\mathbf {X} }^{2}+\left(1-{\mathit {R}}_{\mathbf {X} }^{2}\right)r_{yz}^{*2}$ .

beträgt. Folglich kann das Bestimmtheitsmaß durch die Aufnahme zusätzlicher erklärender Variablen nicht sinken. Hierbei stellt ${\mathit {R}}_{\mathbf {X} z}$ das Bestimmtheitsmaß in der Regression von auf ${\mathbf {X}}$ und einer zusätzlichen Variable dar. ${\mathit {R}}_{\mathbf {X} }^{2}$ ist das Bestimmtheitsmaß für die Regression von auf ${\mathbf {X}}$ alleine und $r_{yz}^{*2}$ ist die partielle Korrelation zwischen und , wenn man für ${\mathbf {X}}$ kontrolliert. Wenn man immer weitere Variablen in das Model hinzufügt, wird der R-Quadrat-Wert weiter ansteigen, bis hin zur oberen Grenze . Daher sollte das adjustierte Bestimmtheitsmaß herangezogen werden, das die Aufnahme jeder neu hinzugenommenen erklärenden Variable „bestraft“.

In Matrixschreibweise ist das adjustierte Bestimmtheitsmaß gegeben durch den Quotienten aus dem „mittleren Residuenquadrat“ und dem „mittleren Quadrat der totalen Abweichungen“:

${\overline {\mathit {R}}}{}^{2}=1-{\frac {{\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}}/(n-p)}{\mathbf {y} ^{\top }\mathbf {y} -n{\overline {y}}^{2}/(n-1)}}=1-{\frac {{\hat {\sigma }}^{2}}{{\hat {\sigma }}_{\mathbf {y} }^{2}}}$ ,

wobei

${\hat {\sigma }}^{2}={\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}}/(n-p)\quad$ und $\quad {\hat {\sigma }}_{\mathbf {y} }^{2}=\mathbf {y} ^{\top }\mathbf {y} -n{\overline {y}}^{2}/(n-1)$

die unverzerrten Schätzer für die Varianzen von ${\boldsymbol {\varepsilon }}$ und $\mathbf{y}$ darstellen.

Bestimmtheitsmaß bei Heteroskedastizität

Wenn die Anpassung durch die verallgemeinerte Kleinste-Quadrate-Schätzung erfolgt, können alternative Versionen des Bestimmtheitsmaßes entsprechend diesem statistischen Rahmenwerk berechnet werden, während das „einfache“ Bestimmtheitsmaß immer noch nützlich sein kann, da es einfacher zu interpretieren ist. Das Bestimmtheitsmaß bei vorliegen von Heteroskedastizität ist durch die gewichteten Summen der Abweichungsquadrate wie folgt definiert

${\mathit {R}}_{GSQ}^{2}\equiv 1-{\frac {GSQR}{GSQT}}$ ,

wobei $GSQR$ die „gewichtete Residuenquadratsumme“ (englisch weighted sum of squares residual, kurz: WSSR) und $GSQT$ die „gewichtete totale Quadratsumme“ (englisch weighted sum of squares total, kurz: WSST) darstellt. Im verallgemeinerten linearen Regressionsmodell, also bei Vorliegen einer nichtskalaren Kovarianzmatrix der Störgrößen $\mathbf {\Phi } =\sigma ^{2}\mathbf {\Psi }$ mit der Gewichtsmatrix $\mathbf {G} =\mathbf {\Psi } ^{-1}$ , ist ${\mathit {R}}_{GSQ}^{2}$ gegeben durch:

${\mathit {R}}_{\mathbf {\Psi } ^{-1}}^{2}={\frac {\mathbf {y} ^{\top }\mathbf {\Psi } ^{-1}\mathbf {X} \mathbf {b} _{\mathbf {\Psi } ^{-1}}-(({\mathbf {\Psi } ^{-1}})^{\top }\mathbf {y} )^{2}/({\mathbf {\Psi } ^{-1}})^{\top }\mathbf {1} }{\mathbf {y} ^{\top }\,\mathbf {\Psi } ^{-1}\mathbf {y} -(({\mathbf {\Psi } ^{-1}})^{\top }\mathbf {y} )^{2}/({\mathbf {\Psi } ^{-1}})^{\top }\mathbf {1} }}$ ,

wobei

$\mathbf {b} _{\mathbf {\Psi } ^{-1}}=\left(\mathbf {X} ^{\top }\mathbf {\Psi } ^{-1}\mathbf {X} \right)^{-1}\mathbf {X} ^{\top }\mathbf {\Psi } ^{-1}\mathbf {y}$

den verallgemeinerten Kleinste-Quadrate-Schätzer darstellt.

Interpretation der Varianz der Regressionsparameter

Die Kovarianzmatrix des Kleinste-Quadrate-Schätzvektors ${\mathbf b}$ ist gegeben durch $\mathbf {\Sigma } _{\mathbf {b} }=\sigma ^{2}(\mathbf {X} ^{\top }\mathbf {X} )^{-1}$ .^{[A
11]} Die Diagonalelemente dieser Kovarianzmatrix stellen die Varianzen $\operatorname {Var} (b_{j})$ der jeweiligen Regressionsparameter dar. Es kann gezeigt werden, dass sich die Varianzen auch darstellen lassen als

$\operatorname {Var} (b_{j})={\frac {\sigma ^{2}}{(1-{\mathit {R}}_{j}^{2})\sum \nolimits _{i=1}^{n}(x_{ij}-{\overline {x}}_{j})^{2}}}$ ,

wobei ${\mathit {R}}_{j}^{2}$ das Bestimmtheitsmaß einer Hilfsregression ist, bei der die erklärende Variable $x_{j}$ (hier als abhängige Variable) auf alle anderen erklärenden Variablen (inkl. Absolutglied) regressiert wird. Je größer ceteris paribus die lineare Abhängigkeit einer erklärenden Variablen $x_{j}$ mit anderen erklärenden Variablen ist (Multikollinearität, gemessen durch ${\mathit {R}}_{j}^{2}$ , desto größer ist die Varianz. Im Extremfall ${\mathit {R}}_{j}^{2}\rightarrow 1$ geht die Varianz gegen Unendlich.

Diese Varianzformel liefert mithilfe der Varianzinflationsfaktors

$\operatorname {VIF} _{j}\equiv {\frac {1}{1-{\mathit {R}}_{j}^{2}}}\in \left[1;\infty \right)$

ebenfalls ein Diagnosewerkzeug, um den Grad der Multikollinearität zu messen. Der Varianzinflationsfaktor quantifiziert einen Anstieg der Varianz von $\beta_j$ aufgrund der linearen Abhängigkeit von $x_{j}$ mit den restlichen erklärenden Variablen. Je größer die Korrelation zwischen $x_{j}$ und den anderen erklärenden Variablen ist, desto größer ist ${\mathit {R}}_{j}^{2}$ und damit der Varianzinflationsfaktor.

Mithilfe des Standardfehlers der Residuen, lassen sich Konfidenzintervalle konstruieren. Ersetzt man bei der Standardabweichung des jeweiligen Parameterschätzers ${\sqrt {\operatorname {Var} (b_{j})}}$ das unbekannte $\sigma$ durch das bekannte $\hat{\sigma}$ ergibt sich der Standardfehler des Regressionskoeffizienten $b_{j}$ durch

$\operatorname {SE} (b_{j})={\sqrt {\frac {{\tfrac {1}{n-p}}\sum \nolimits _{i=1}^{n}{\hat {\varepsilon }}_{i}^{2}}{(1-{\mathit {R}}_{j}^{2})\sum \nolimits _{i=1}^{n}(x_{ij}-{\overline {x}}_{j})^{2}}}}$ .

Die Größe der Standardfehler der geschätzten Regressionsparameter hängt also von der Residualvarianz, der Abhängigkeit der erklärenden Variablen untereinander und der Streuung der jeweiligen erklärenden Variablen ab.

R-Quadrat-Schreibweise der F-Statistik

Die allgemeine Form der F-Statistik ist definiert durch den relativen Zuwachs in der Residuenquadratsumme beim Übergang vom unrestringierten zum restringierten Modell

$F\equiv {\frac {\left(SQR_{H_{0}}-SQR\right)/q}{SQR/(n-k-1)}}$ ,

wobei die Anzahl der zu testenden Restriktionen darstellt. Beim Testen von Restriktionen ist es oft von Vorteil eine Darstellung der F-Statistik zu haben, bei der die Bestimmtheitsmaße des restringierten Modells und des unrestringierten Modells miteinbezogen werden. Ein Vorteil dieser Darstellung ist, dass das die Residuenquadratsumme sehr groß und deren Berechnung damit umständlich sein kann. Das Bestimmtheitsmaß dagegen liegt immer zwischen $0$ und . Die R-Quadrat-Schreibweise der F-Statistik ist gegeben durch

$F={\frac {\left({\mathit {R}}{}^{2}-{\mathit {R}}{}_{H_{0}}^{2}\right)/q}{\left(1-{\mathit {R}}{}^{2}\right)/(n-p)}}$ ,

wobei der Umstand genutzt wurde, dass für die Residuenquadratsumme des restringierten und des unrestringierten Modells gilt

$SQR_{H_{0}}=SQT\left(1-{\mathit {R}}{}_{H_{0}}^{2}\right)\quad$ und $\quad SQR=SQT\left(1-{\mathit {R}}{}^{2}\right)$ .

Da das Bestimmtheitsmaß im Gegensatz zu Residuenquadratsumme in jedem Regressionsoutput ausgegeben wird, kann man leicht die Bestimmtheitsmaße des restringierten Modells und des unrestringierten Modells benutzen, um auf Variablenexklusion zu testen.

Test auf Gesamtsignifikanz eines Modells

→ Hauptartikel: Globaler F-Test

Der globale F-Test prüft, ob mindestens eine Variable einen Erklärungsgehalt für das Modell liefert. Falls diese Hypothese verworfen wird, ist das Modell nutzlos. Dieser Test lässt sich so interpretieren, als würde man die gesamte Anpassungsgüte der Regression, also das Bestimmtheitsmaß ${\mathit {R}}^{2}$ der Regression, testen. Die Null- und die Alternativhypothese lauten:

$H_{0}\colon \beta _{1}=\beta _{2}=\ldots =\beta _{k}\;=\;0\Rightarrow {\mathit {R}}_{H_{0}}^{2}=0$ gegen $H_{1}:\beta _{j}\;\neq \;0\;\mathrm {f{\ddot {u}}r\;mindestens\;ein} \;j\in \{1,\ldots ,k\}\Rightarrow {\mathit {R}}^{2}>0$

und die Teststatistik dieses Tests ist gegeben durch

${\begin{aligned}F={\frac {{\mathit {R}}^{2}}{1-{\mathit {R}}^{2}}}{\frac {n-p}{k}}\;{\stackrel {H_{0}}{\sim }}\;F\left(k,n-p\right)\end{aligned}}$ .

Das Modell unter der Nullhypothese $H_{0}$ ist dann das sogenannte Nullmodell (Modell, das nur aus einer Regressionskonstanten $\beta _{0}$ besteht). Die Teststatistik ist unter der Nullhypothese F-verteilt mit und $(n-p)$ Freiheitsgraden.^{[A
12]} Überschreitet der empirische F-Wert bei einem a priori festgelegten Signifikanzniveau $\alpha$ den kritischen F-Wert $F_{(1-\alpha )}(k,n-p)$ (das $(1-\alpha)$ -Quantil der F-Verteilung mit und $(n-p)$ Freiheitsgraden) so verwirft man die Nullhypothese, dass alle Steigungsparameter des Modells gleich null sind. Das Bestimmtheitsmaß ist dann ausreichend groß und mindestens eine erklärende Variable trägt vermutlich genügend Information zur Erklärung der abhängigen Variablen bei. Es ist naheliegend, bei hohen F-Werten die Nullhypothese zu verwerfen, da ein hohes Bestimmtheitsmaß zu einem hohen F-Wert führt. Wenn der Wald-Test für eine oder mehrere erklärende Variablen die Nullhypothese ablehnt, dann kann man davon ausgehen, dass die zugehörigen Regressionsparameter ungleich Null sind, so dass die Variablen in das Modell mit einbezogen werden sollten.

Es kann gezeigt werden, dass unter der obigen Nullhypothese sich für das Bestimmtheitsmaß im Mittel

$\mathbb {E} \left({\mathit {R}}^{2}\right)={\frac {k}{n-1}}$

ergibt. Daraus folgt, dass wenn $n=k+1=p$ , dann ist $\mathbb {E} \left({\mathit {R}}^{2}\right)=1$ , d.h. die bloße Größe des R-Quadrat-Wertes ist bei kleinen Stichprobengrößen ein schlechter Indikator für die Anpassungsgüte.

Zusammenhang zwischen adjustiertem Bestimmtheitsmaß, F-Test und t-Test

Direkt aus der obigen Definition von ${\overline {\mathit {R}}}{}^{2}$ folgt

${\frac {SQR/(n-k-1)}{SQT/(n-1)}}=1-{\overline {\mathit {R}}}{}^{2}$ .

Wenn man diesen Ausdruck nun nach $SQR$ auflöst ergibt sich $SQR=(n-k-1)(1-{\overline {R}}{}^{2})SQT/(n-1)$ . Analog dazu gilt für das adjustierte Bestimmtheitsmaß des Nullhypothesenmodells, welches nur $k-q$ erklärende Variablen besitzt $SQR_{H_{0}}=(n-k-1+q)\left(1-{{\overline {\mathit {R}}}{}^{2}}_{H_{0}}\right)SQT/(n-1)$ .

Bei einsetzen der beiden Größen in den F-Wert

$F\equiv {\frac {\left(SQR_{H_{0}}-SQR\right)/q}{SQR/(n-k-1)}}\;{\stackrel {H_{0}}{\sim }}\;F(q,n-p)$ .

ergibt sich durch algebraische Umformungen

$F={\frac {(n-k-1)\left({\overline {\mathit {R}}}{}^{2}-{\overline {\mathit {R}}}{}_{H_{0}}^{2}\right)/q+\left(1-{\overline {\mathit {R}}}{}_{H_{0}}^{2}\right)}{1-{\overline {\mathit {R}}}{}^{2}}}$ .

Als Folge daraus ist der F-Wert genau dann größer als , wenn

$(n-k-1)\left({\overline {\mathit {R}}}{}^{2}-{\overline {\mathit {R}}}{}_{H_{0}}^{2}\right)/q+\left(1-{\overline {\mathit {R}}}{}_{H_{0}}^{2}\right)>1-{\overline {\mathit {R}}}{}^{2}$ .

Durch Umstellen erhält man

$\left({\overline {\mathit {R}}}{}^{2}-{\overline {\mathit {R}}}{}_{H_{0}}^{2}\right)>-\left({\overline {\mathit {R}}}{}^{2}-{\overline {\mathit {R}}}{}_{H_{0}}^{2}\right)q/(n-k-1)$ .

Diese Ungleichung ist genau dann erfüllt, wenn ${\overline {\mathit {R}}}{}^{2}>{\overline {\mathit {R}}}{}_{H_{0}}^{2}$ . Anders ausgedrückt übersteigt das adjustierte Bestimmtheitsmaß des unrestringiertes Modells das adjustierte Bestimmtheitsmaß des restringierten Modells genau dann wenn der F-Wert des F-Tests größer als ist. Der t-Test stellt einen Spezialfall des F-Tests dar. Er ergibt sich im Fall einer Restriktion q=1 . Für die Teststatistik eines solchen Tests gilt, dass die quadrierte t-Statistik der F-Statistik entspricht $t^{2}=F$ . Die obige Ungleichung ist für einen t-Test ebenso erfüllt, genau dann wenn $t^{2}>1$ .

Verallgemeinerung mittels Zielfunktion

Ein weiterer Ansatz stellt die Verallgemeinerung des Bestimmtheitsmaßes mittels einer anderen Zielfunktionen als die Residuenquadratsumme dar. Sei $Q_{N}(\mathbf {\theta } )$ die Zielfunktion, die es zu maximieren gilt, Q_0 stellt den Wert in einem Leermodell dar, $Q_{\text{fit}}$ bezeichnet den Wert im angepassten Modell, und $Q_{\text{max}}$ bezeichnet den größtmöglichen Wert von $Q_{N}(\mathbf {\theta } )$ . Der maximale potentielle Zuwachs in der Zielfunktion, der durch die Hinzunahme von erklärenden Variablen resultiert ist $Q_{\text{max}}-Q_{0}$ . Im Gegensatz dazu stellt der gegenwärtige Zuwachs $Q_{\text{fit}}-Q_{0}$ dar. Die Verallgemeinerung des Bestimmtheitsmaßes mittels Zielfunktionen ergibt sich dann durch

${\mathit {R}}_{\text{RZ}}^{2}={\frac {Q_{\text{fit}}-Q_{0}}{Q_{\text{max}}-Q_{0}}}=1-{\frac {Q_{\text{max}}-Q_{\text{fit}}}{Q_{\text{max}}-Q_{0}}}$ .

Hier bei bedeutet das Subskript ${\text{RZ}}$ „relativer Zuwachs“. Bei der Kleinste-Quadrate-Schätzung ist die maximierte Verlustfunktion $-SQR$ . Dann ist $Q_{0}=-SQT$ , $Q_{\text{fit}}=-SQR$ und $Q_{\text{max}}=0$ , und somit gilt für das Bestimmtheitsmaß bei der Kleinste-Quadrate-Schätzung ${\mathit {R}}_{\text{RZ}}^{2}=SQE/SQT$ . Die Vorteile dieser Verallgemeinerung mittels Zielfunktionen sind, dass das Maß ${\mathit {R}}_{\text{RZ}}^{2}$ zwischen Null und Eins liegt und steigt, wenn weitere erklärende Variablen dem Modell hinzugefügt werden. Wenn $Q_{\text{max}}=0$ (dies ist beispielsweise bei binären diskreten Entscheidungsmodellen und multinomialen Modellen der Fall), dann ergibt sich die verwandte Maßzahl ${\mathit {R}}_{Q}^{2}=1-Q_{\text{fit}}/Q_{0}$ .

Pseudo-Bestimmtheitsmaß

Im Falle einer linearen Regression mit einer abhängigen metrischen Variablen wird die Varianz dieser Variablen benutzt um die Güte des Regressionsmodells zu beschreiben. Bei einem nominalen oder ordinalen Skalenniveau von existiert jedoch kein Äquivalent, da man die Varianz und damit ein Bestimmtheitsmaß nicht berechnen kann. Für diese wurden verschiedene Pseudo-Bestimmtheitsmaße vorgeschlagen, beispielsweise Maße die auf der logarithmischen Plausibilitätsfunktion (log-Likelihood-Funktion) basieren, wie z.B. das Pseudo-Bestimmtheitsmaß nach McFadden

${\mathit {R}}_{\text{McFadden}}^{2}\equiv 1-{\frac {\ln L_{1}}{\ln L_{0}}}$ (für eine Erläuterung der Notation siehe Maße die auf der logarithmischen Plausibilitätsfunktion basieren).

Bei nichtlinearen Modellen werden Pseudo-Bestimmtheitsmaße verwendet. Allerdings gibt es kein universelles Pseudo-Bestimmtheitsmaß. Je nach Kontext müssen andere Pseudo-Bestimmtheitsmaße herangezogen werden.

Prognose-Bestimmtheitsmaß

Während das Bestimmtheitsmaß, das adjustierte Bestimmtheitsmaß oder auch die Pseudo-Bestimmtheitsmaße eine Aussage über die Modellgüte machen, zielt das Prognose-Bestimmtheitsmaß auf die Vorhersagequalität des Modells. Im Allgemeinen wird das Prognose-Bestimmtheitsmaß kleiner als das Bestimmtheitsmaß sein.

Zunächst wird der Wert des PRESS-Kriteriums, also die prädiktive Residuenquadratsumme (engl.: predictive residual error sum of squares) berechnet

${\text{PRESS}}\equiv \sum \limits _{i=1}^{n}(y_{i}-{\hat {y}}_{i,-i})^{2}$ .

Hierbei ist $y_{i}$ der beobachtete Wert und $\hat{y}_{i,-i}$ der Wert, der sich als Schätzung von $y_{i}$ ergibt, wenn alle Beobachtungen außer der -ten in das Regressionsmodell einfließen. Zur Berechnung des der prädiktiven Residuenquadratsumme müssten daher lineare Regressionsmodelle mit jeweils (n-1) Beobachtungen berechnet werden.

Es lässt sich jedoch zeigen, dass das Residuum $(y_{i}-{\hat {y}}_{i,-i})$ aus den „gewöhnlichen Residuen“ $(y_{i}-{\hat {y}}_{i})$ (bei Benutzung aller Beobachtungen) berechnet werden kann. Das Prognose-Bestimmtheitsmaß ergibt sich dann als

${\mathit {R}}_{\text{prog.}}^{2}\equiv 1-{\frac {\text{PRESS}}{\sum \nolimits _{i=1}^{n}(y_{i}-{\overline {y}})^{2}}}$ .

Mehrgleichungsmodelle

Für Mehrgleichungsmodelle lässt sich ein Bestimmtheitsmaß wie folgt definieren:

${\mathit {R}}_{I}^{2}\equiv 1-{\frac {({\bar {\mathbf {y} }}-{\bar {\mathbf {X} }}{\tilde {\bar {\boldsymbol {\beta }}}})^{\top }({\hat {\mathbf {\Sigma } }}^{-1}\otimes \mathbf {I} )({\bar {\mathbf {y} }}-{\bar {\mathbf {X} }}{\tilde {\bar {\boldsymbol {\beta }}}})}{Q_{g}(\mathbf {0} )}}$ ,

wobei $({\bar {\mathbf {y} }}-{\bar {\mathbf {X} }}{\tilde {\bar {\boldsymbol {\beta }}}})^{\top }({\hat {\mathbf {\Sigma } }}^{-1}\otimes \mathbf {I} )({\bar {\mathbf {y} }}-{\bar {\mathbf {X} }}{\tilde {\bar {\boldsymbol {\beta }}}})=Q_{g}({\tilde {\bar {\boldsymbol {\beta }}}})$ die Residuenquadratsumme der durchführbaren verallgemeinerten KQ-Schätzung ist und $Q_{g}(\mathbf {0} )$ für $Q_{g}({\tilde {\bar {\boldsymbol {\beta }}}})$ steht im Fall, dass ${\boldsymbol {\beta }}$ nur aus einem Absolutglied besteht.

Bestimmtheitsmaß in R

Als einfaches Beispiel zur Berechnung des Bestimmtheitsmaßes in R wird zunächst der Korrelationskoeffizient zweier Datenreihen berechnet:

# Groesse wird als numerischer Vektor
# durch den Zuweisungsoperator "<-" definiert:
Groesse <- c(176, 166, 172, 184, 179, 170, 176)

# Gewicht wird als numerischer Vektor definiert:
Gewicht <- c(65, 55, 67, 82, 75, 65, 75)

# Berechnung des Bravais-Pearson-Korrelationskoeffizient mit der Funktion "cor":
cor(Gewicht, Groesse, method = "pearson")

Anschließend wird, um das Bestimmtheitsmaß zu erhalten, der Bravais-Pearson-Korrelationskoeffizient quadriert:

# Das Bestimmtheitsmaß ist bei einer erklärenden Variablen das Quadrat des Korrelationskoeffizienten "cor":
cor(Gewicht, Groesse, method = "pearson")^2

# Bei Ausführung ergibt sich ein ''R''-Quadrat-Wert von 0,864, d. h. 86,40 % der Streuung im Körpergewicht kann durch die lineare Regression von Körpergewicht auf Körpergröße erklärt werden.

Grafikausgabe des Beispiels

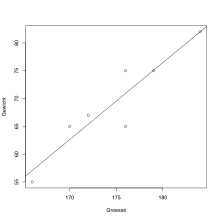
Mithilfe der Statistiksoftware R kann eine einfache lineare Regression durchgeführt werden. Dies kann in R durch die Funktion lm ausgeführt werden, wobei die abhängige Variable von den unabhängigen Variablen durch die Tilde getrennt wird. Die Funktion summary gibt die Koeffizienten der Regression und weitere Statistiken, wie z.B. das adjustierte Bestimmtheitsmaß, hierzu aus:

# Lineare Regression mit Gewicht als Zielvariable
# Ergebnis wird als reg gespeichert:
reg <- lm(Gewicht ~ Groesse)

# Ausgabe der Ergebnisse der obigen linearen Regression:
summary(reg)

Literatur

Ludwig Fahrmeir, Thomas Kneib, Stefan Lang: Regression: Modelle, Methoden und Anwendungen.. Auflage. Springer Verlag, 2009, ISBN 978-3-642-01836-7.
J. Neter, M. H. Kutner, C.J. Nachtsheim, W. Wasserman: Applied linear statistical models. 4. Auflage. McGraw-Hill 1996.
M.-W. Stoetzer: Regressionsanalyse in der empirischen Wirtschafts- und Sozialforschung – Eine nichtmathematische Einführung mit SPSS und Stata. Berlin 2017, ISBN 978-3-662-53823-4.

Anmerkungen

↑ Die durch die Kleinste-Quadrate-Schätzung gewonnenen Parameterschätzer ${\hat {\beta }}_{0}$ und ${\hat {\beta }}_{1}$ werden oft auch als $b_{0}$ und $b_{1}$ notiert.
↑ Es gibt in der Literatur keinen Konsens hinsichtlich der Abkürzungen ${\text{SST}}$ , $\textstyle {\text{SSE}}$ und ${\text{SSR}}$ . Die „totale Quadratsumme“ (sum of squares total) wird oft statt ${\text{SST}}$ auch als ${\text{TSS}}$ abgekürzt. Unglücklicherweise wird die „durch die Regression erklärte Quadratsumme“ (sum of squares explained), hier abgekürzt als ${\text{SSE}}$ , manchmal als „Quadratsumme der Regression“ (sum of squares regression) bezeichnet und damit als ${\text{SSR}}$ abgekürzt. Wenn dieser Ausdruck jedoch mit seiner natürlichen Abkürzung ${\text{SSR}}$ abgekürzt wird, kann er leicht mit der „Residuenquadratsumme“ (sum of squares residual) verwechselt werden, die ebenfalls mit ${\text{SSR}}$ abgekürzt wird. Manche statistischen Programmpakete bezeichnen die „erklärte Quadratsumme“ (sum of squares explained) auch als „Modellquadratsumme“ (sum of squares model). Die Abkürzungsproblematik wird dadurch verschärft, dass die „Residuenquadratsumme“ oft auch als „Fehlerquadratsumme“ (sum of squares errors) bezeichnet wird (diese Bezeichnung ist besonders irreführend, da Störgrößen bzw. Fehler und Residuen unterschiedliche Größen sind).
↑ Der Begriff Bestimmtheitsmaß ist eine Komposition aus den beiden Grundbegriffen der philosophischen Logik: Bestimmtheit und Maß. Der Begriff der (inneren) Bestimmtheit bezeichnet in der philosophischen Logik die „Qualität“ bzw. „Güte“ eines Dings und das Maß eine „qualitative Quantität“.
↑ Zur Vereinfachung werden im Artikel bei allgemeinen Definitionen die Summationsgrenzen weggelassen.
↑ Die Bezeichnung Streuungszerlegung charakterisiert das Wesen, aber nicht den mathematischen Vorgang, indem nicht die Streuung, sondern die totale Quadratsumme zerlegt wird.
↑ Dies gilt, wegen $\displaystyle \sum \nolimits _{i=1}^{n}({\hat {y}}_{i}-{\overline {\hat {y}}})^{2}=\displaystyle \sum \nolimits _{i=1}^{n}((b_{0}+b_{1}x_{i})-(b_{0}+b_{1}{\overline {x}}))^{2}=\displaystyle \sum \nolimits _{i=1}^{n}(b_{1}(x_{i}-{\overline {x}}))^{2}=b_{1}^{2}\displaystyle \sum \nolimits _{i=1}^{n}\left(x_{i}-{\overline {x}}\right)^{2}$ .
↑ Im Allgemeinen ist der Standardfehler der Regression gegeben durch ${\hat {\sigma }}={\sqrt {{\tfrac {1}{n-p}}{\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}}}}$ .
↑ Bestimmung der Funktion auf Grundlage der verwendeten Abbildung, Prof. Engelbert Niehaus (Uni Koblenz) – Koeffizienten und Typ der Abbildung wurden aus dem Diagramm abgelesen, um Abbildung und Funktionsterm konsistent zu halten. Bestimmung der Koeffizienten von dem Funktionsterm $\textstyle f(x)\equiv -{\tfrac {4}{3}}|x-0{,}9|+1{,}4$ erfolgte, um die nebenstehende Abbildung nicht verändern zu müssen.
↑ Bestimmung der quadratischen Funktion auf Grundlage der verwendeten Abbildung, Prof. Engelbert Niehaus (Uni Koblenz) – Koeffizienten und Typ der Abbildung wurden aus dem Diagramm abgelesen, um Abbildung und Funktionsterm konsistent zu halten. Bestimmung der Koeffizienten von dem Funktionsterm $\textstyle g(x)\equiv 1{,}1x^{2}-1{,}1$ erfolgte, um die nebenstehende Abbildung nicht verändern zu müssen.
↑ Für Populationsgrößen werden konventionell griechische Buchstaben und für Stichprobengrößen lateinische Buchstaben verwendet.
↑ Die wahre Kovarianzmatrix kann in Anwendungen nicht berechnet werden, da die Varianz der Störgrößen $\sigma ^{2}$ unbekannt ist.
↑ Mit ${\stackrel {H_{0}}{\sim }}$ ist die Verteilung der Teststatistik unter der Nullhypothese gemeint.

Basierend auf einem Artikel in:

Wikipedia.de